Anti-Durer ⁠

Albrecht Dürer, 1471—1528 fu un grande artista tedesco. Egli si occupò anche di questioni teoriche riguardanti le arti figurative e, in particolare, studiò il problema della prospettiva. Parte del suo libro del 1525 “Istruzioni per l’arte di misurare figure del piano e dello spazio usando riga e compasso” è dedicata allo studio delle proprietà di oggetti geometrici, tra cui i poliedri e i loro sviluppi.

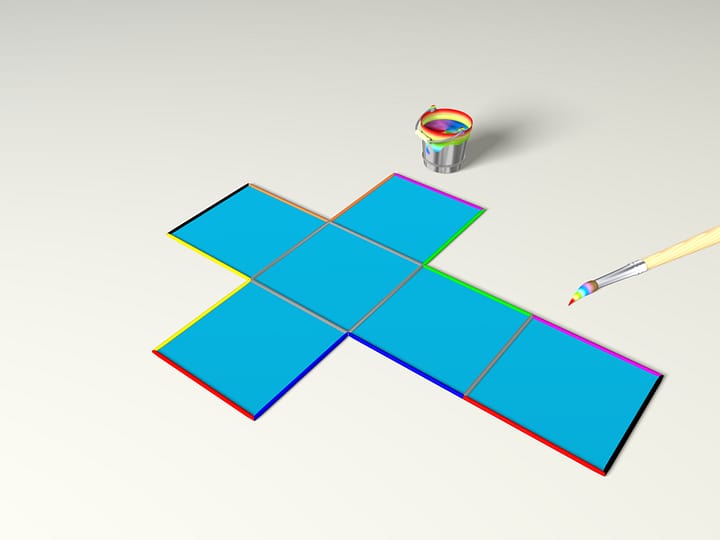
Lo sviluppo di un poliedro lungo gli spigoli consiste nella scelta di poligoni, disposti senza intersezioni su un unico piano, e delle condizioni di incollamento di questi poligoni. Se tagliando in un certo modo un poliedro lungo gli spigoli si riesce ad ottenere un solo poligono, rispettando la condizione di non intersezione, allora tale sviluppo si chiama connesso.

Nelle pagine del suo libro Dürer mostra degli sviluppi connessi di alcuni poliedri, talvolta piuttosto complicati. È poco probabile che egli si sia chiesto se è sempre possibile che basti un unico poligono per rappresentare lo sviluppo di un poliedro, ma la proposizione che segue prende il suo nome. La congettura di Dürer consiste nel supporre che ogni poliedro convesso abbia almeno uno sviluppo connesso lungo gli spigoli.

Ma perché gli sviluppi dei poliedri hanno suscitato un interesse che si protrae da secoli? Il fatto è che lo sviluppo conserva in sé la geometria interna del poliedro e, cioè, proprio quella informazione che può ottenere un essere puntiforme che vive sulla superficie del poliedro e che non ha la possibilità di allontanarsene. In queste condizioni di vita quell’essere ha la sola facoltà di misurare la distanza tra due punti. Usando le sue capacità matematiche, attraverso le distanze, potrà definire gli angoli tra direzioni, calcolare l’area di qualche superficie...

Per alcuni scopi, l’uso dello sviluppo può essere più “comodo” dell’uso del poliedro stesso. Per esempio, se si vuole spedire il modello di un poliedro in un’altra città, allora è neces­sario spedire un pacco. Ma per spedire lo sviluppo del poliedro, è del tutto sufficiente spedire una lettera. Il destinatario, potrà costruirsi da solo il poliedro. Se pensate che il trasporto di poliedri sia un’operazione piuttosto rara, vi sbagliate! Noi tutti lo utilizziamo nella vita quotidiana, quando compriamo un pacchetto di latte o di succo di frutta.

La congettura di Dürer concerne i poliedri convessi. Fino ai nostri giorni, non è stata né dimostrata né confutata. Ma se al problema iniziale non si trova soluzione, vale la pena di cambiare un poco le condizioni e cercare di risolvere il problema modificato. Nel nostro caso è naturale studiare la congettura analoga per una classe più vasta di poliedri, prendendo in considerazione anche i poliedri non convessi.

È facile costruire un poliedro non convesso con facce non neces­sariamente convesse che non ammette alcuno sviluppo connesso. Prendiamo come base una stella non convessa e costruiamo su di essa una piramide. Scegliendo opportunamente gli angoli della stella e l’altezza della piramide, è possibile ottenere che se anche una sola faccia laterale resta collegata alla base nello sviluppo, allora questa intersecherà neces­sariamente la stella. Di conseguenza, la base deve essere scollegata da tutte le facce laterali e lo sviluppo non è più connesso.

Inventare un poliedro non convesso con tutte le facce convesse e non avente alcuno sviluppo connesso lungo gli spigoli non è già tanto facile. Il primo esempio fu costruito soltanto nel 1999.

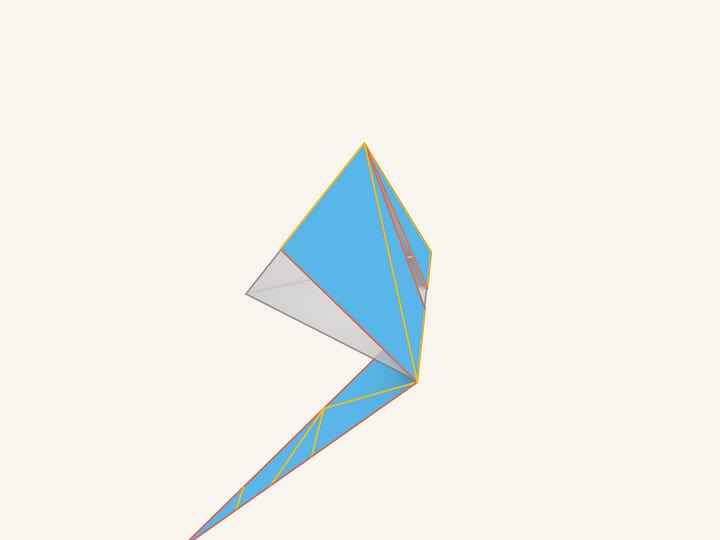
Consideriamo i quattro piccoli tetraedri regolari che si ottengono tagliando un tetraedro vicino ai suoi vertici. Queste piccole piramidi ora le deformiamo, tenendo fissa la loro base (fissata al tetraedro iniziale) e allontanando il vertice dal centro del tetraedro, ottenendo quattro piramidi regolari allungate. Tutte le facce del poliedro non convesso così ottenuto sono poligoni convessi. Se le basi delle piramidi sono abbastanza piccole rispetto alle loro altezze, il poliedro non ammette alcuno sviluppo connesso lungo gli spigoli. Si può mostrare che se il poliedro avesse uno sviluppo connesso lungo gli spigoli, allora almeno una delle sue punte dovrebbe ammettere questo sviluppo, ma non è così. Infatti, consideriamo una “punta” insieme con dei pezzi delle facce del poliedro ad essa connesse. Tutti i possibili sviluppi lungo gli spigoli di questa parte di poliedro, che consistano di in solo pezzo, hanno delle auto–intersezioni.

Ora che abbiamo visto un “contresempio non convesso” alla congettura di Dürer, torniamo alla sua formulazione iniziale, nella classe dei poliedri convessi.

Il più semplice poliedro convesso è la piramide triangolare (o tetraedro), che ha quattro vertici e quattro facce.

Ma persino in questo classe più semplice di poliedri esistono dei rappresentanti per i quali non tutti gli sviluppi lungo gli spigoli sono senza auto–intersezioni. Però tutti hanno anche degli sviluppi connessi. Finora non è stato costruito neppure un poliedro, avente soltanto sviluppi lungo gli spigoli con auto–intersezioni, e consistenti di un unico pezzo.

Non molto tempo fa N. Pю Dolbinin ha formulato una nuova congettura, che ha chiamato “anti–Dürer. Che, cioè, dato un numero intero $k$ arbitrario, esiste un poliedro convesso tale che, per disporre sul piano il suo sviluppo lungo gli spigoli senza intersezioni, occorre suddividerlo in almeno $k$ parti.

Osserviamo che, se la congettura di Dürer è falsa, allora sono possibili due casi sostanzialmente diversi.

Il caso limitato: per qualsiasi poliedro convesso esiste uno sviluppo senza auto–intersezioni che consiste al più di $k$ pezzi. In questo caso il numero minimo $k$ è lo stesso per tutte le classi di poliedri convessi, cioè non dipende dai particolari casi concreti.

Più interes­sante è il caso non limitato: nella classe di tutti i poliedri il numero dei pezzi neces­sari non è superiormente limitato.

La congettura “anti–Dürer ” consiste solo nel supporre che siamo nel caso non limitato.

Da poco il suo analogo nel caso di poliedri non convessi (nel caso non limitato) è stato dimostrato da alcuni matematici russi.

Voi potete provare a costruire un poliedro convesso, per il quale qualsiasi sviluppo connesso lungo gli spigoli contenga auto–intersezioni, oppure a dimostrare che tale poliedro non esiste. E, se avrete successo, una nuova e bella pagina sarà aggiunta alla geometria.