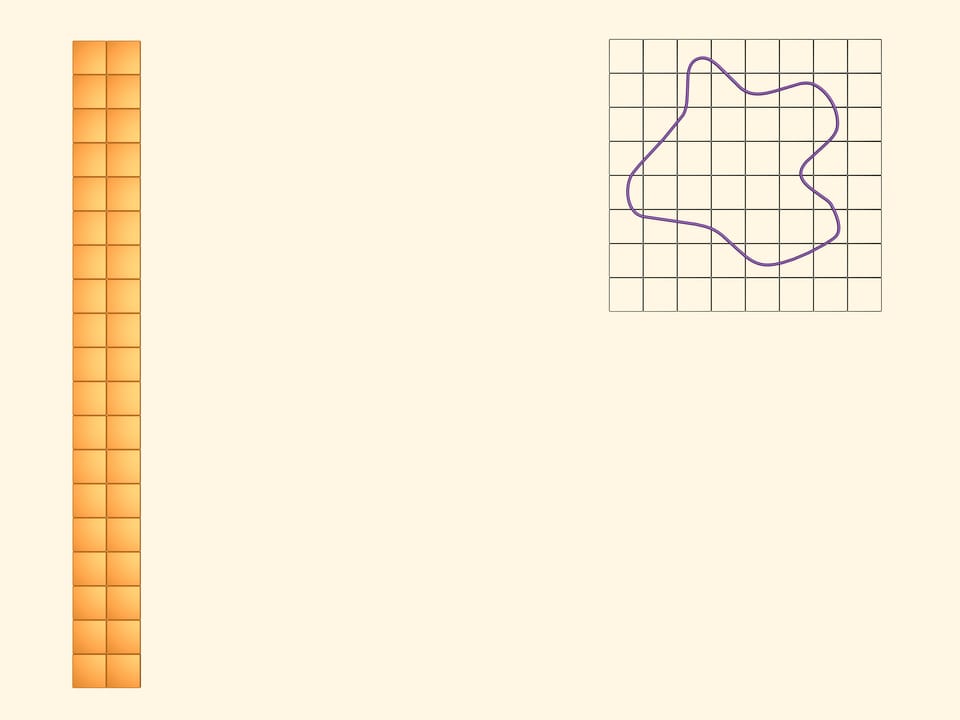
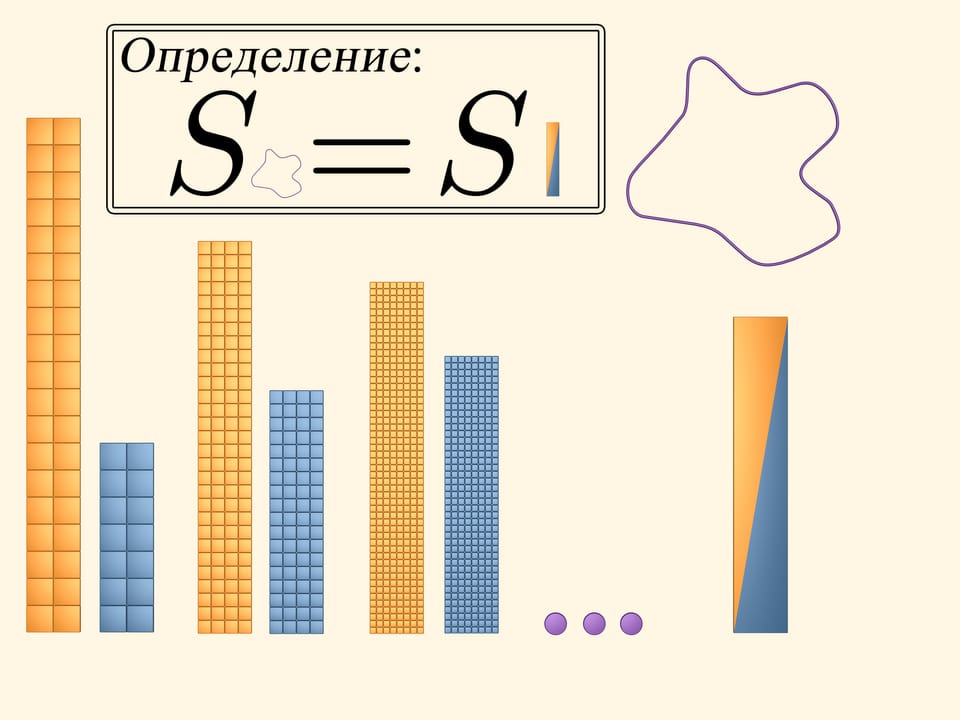
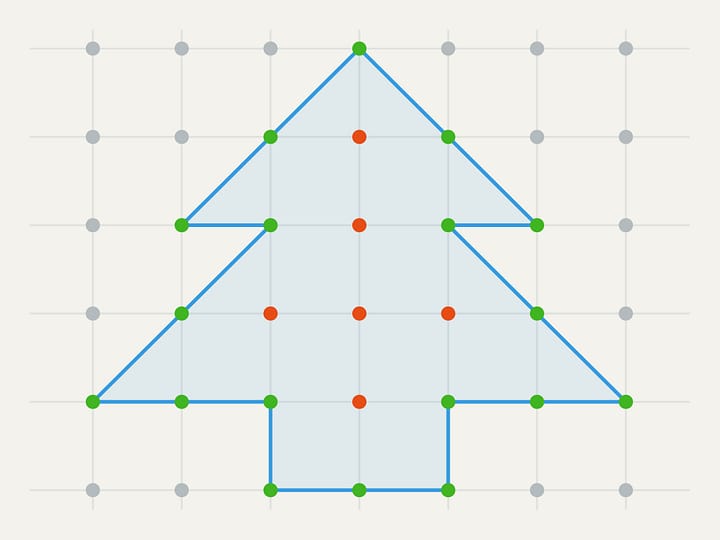
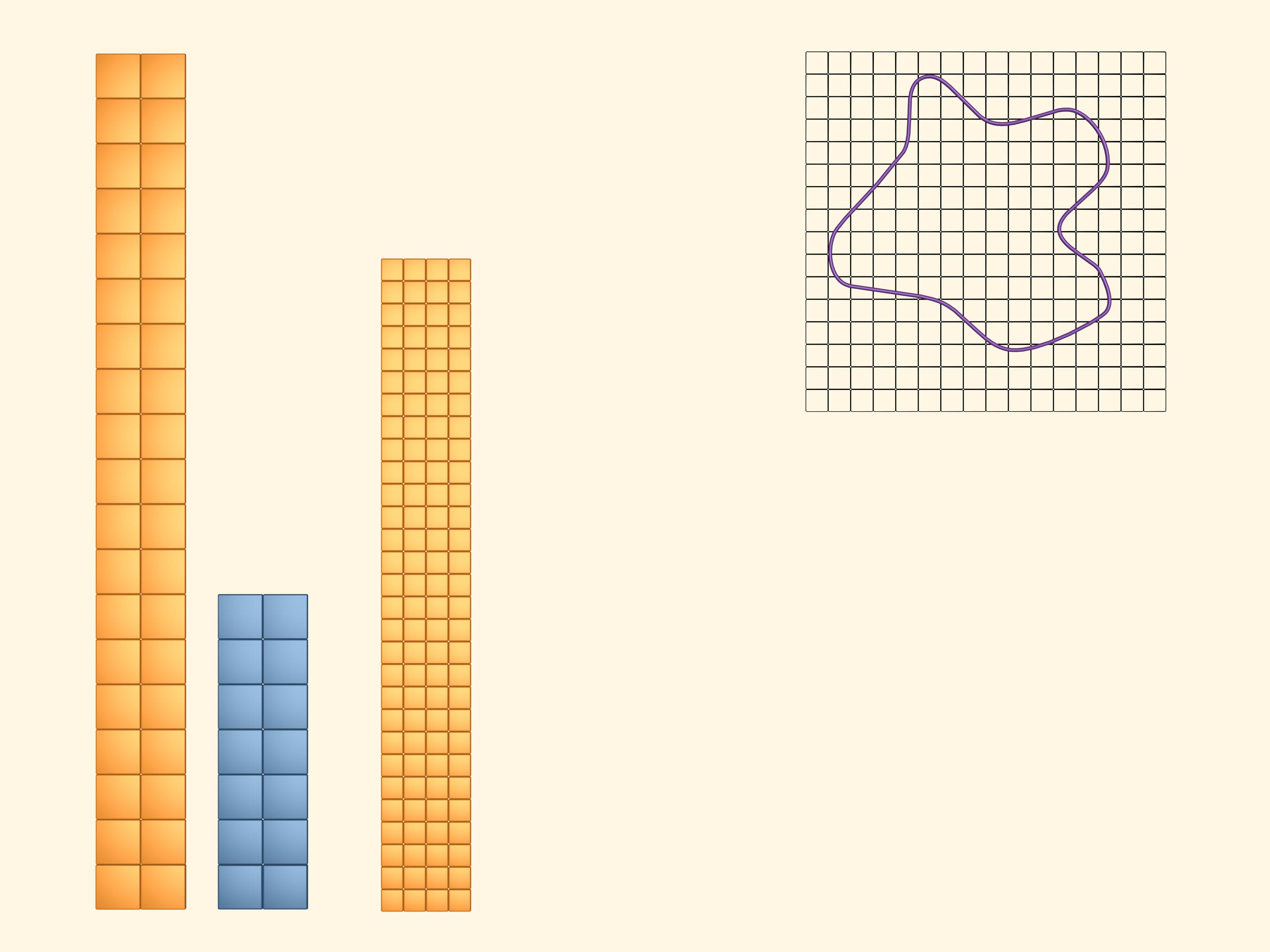L’area del quadrato è uguale al quadrato della lunghezza del suo lato. È facile calcolare l’area di una figura che si può suddividere in diversi quadrati. Ma qual è l’area di una figura limitata da una curva qualunque?
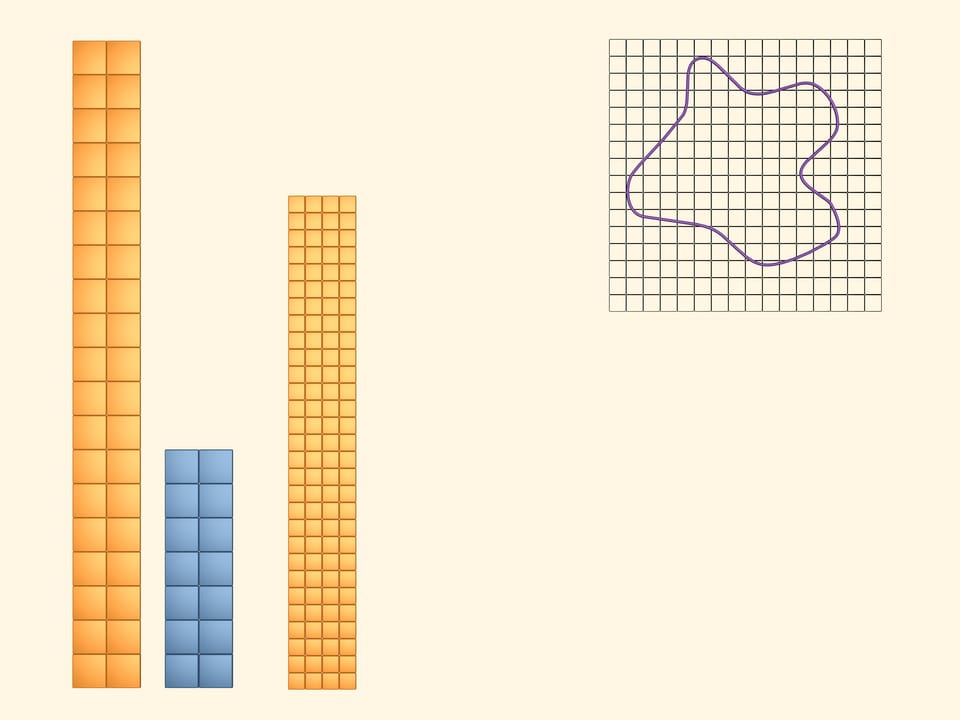
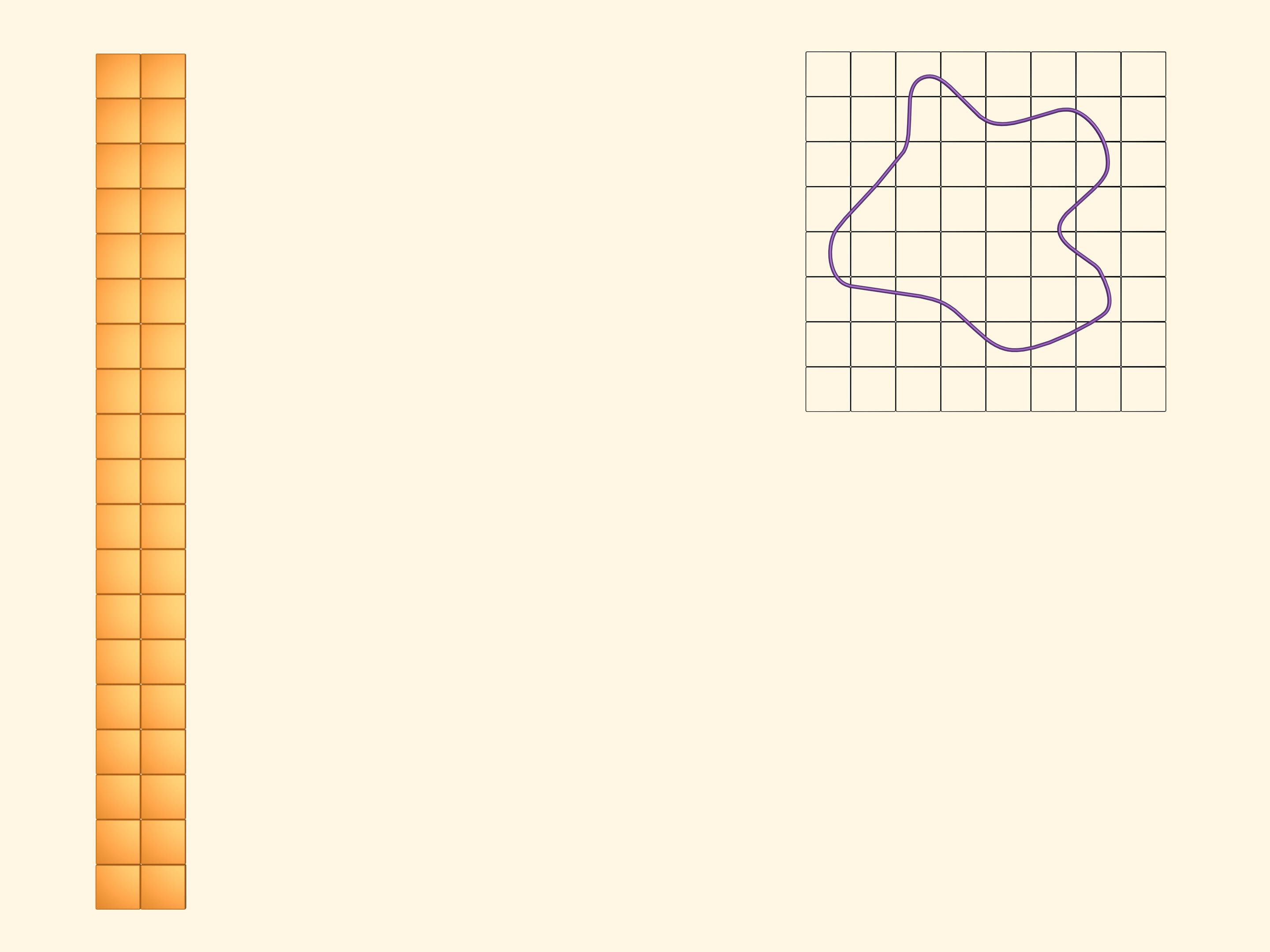
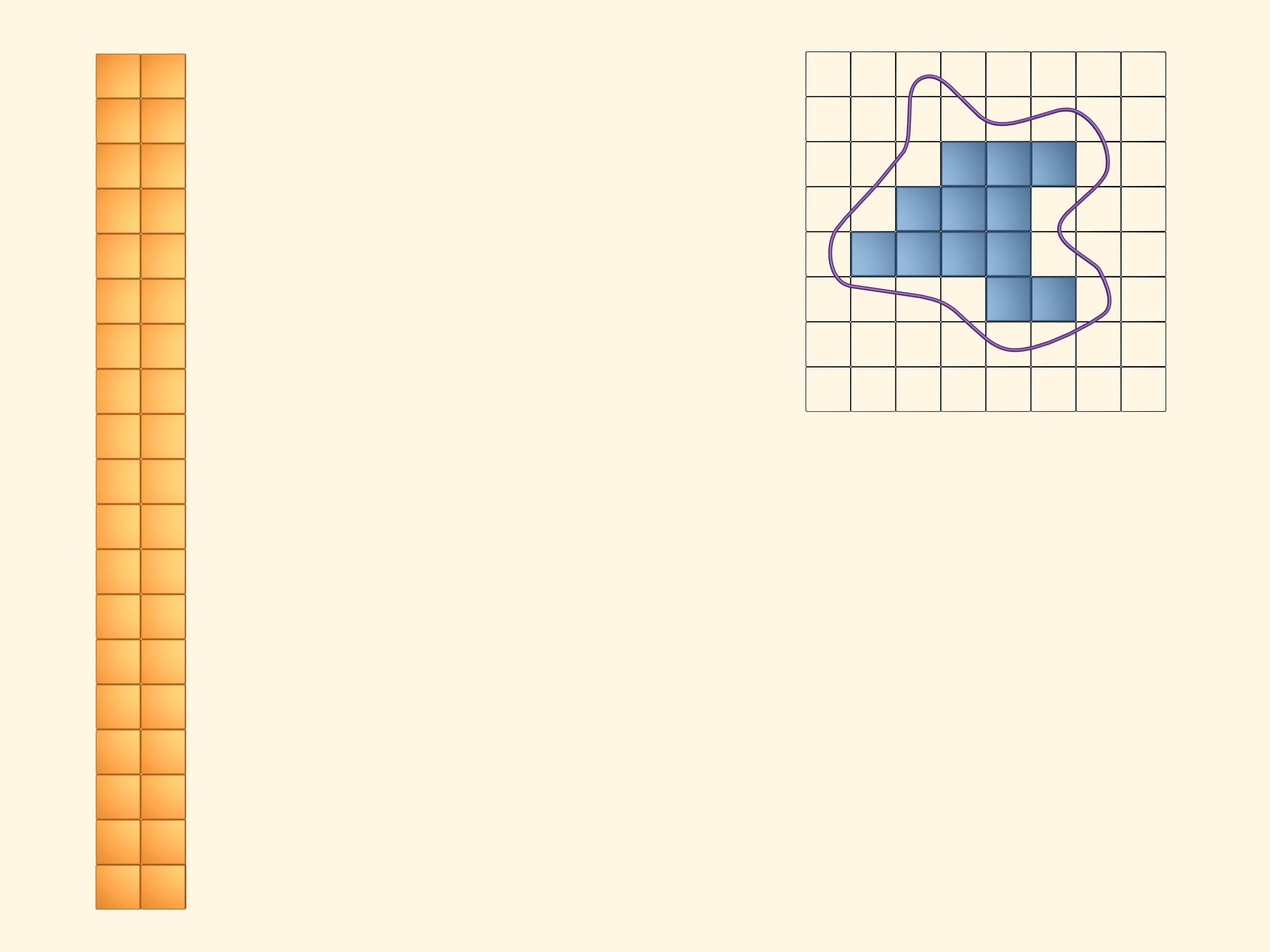
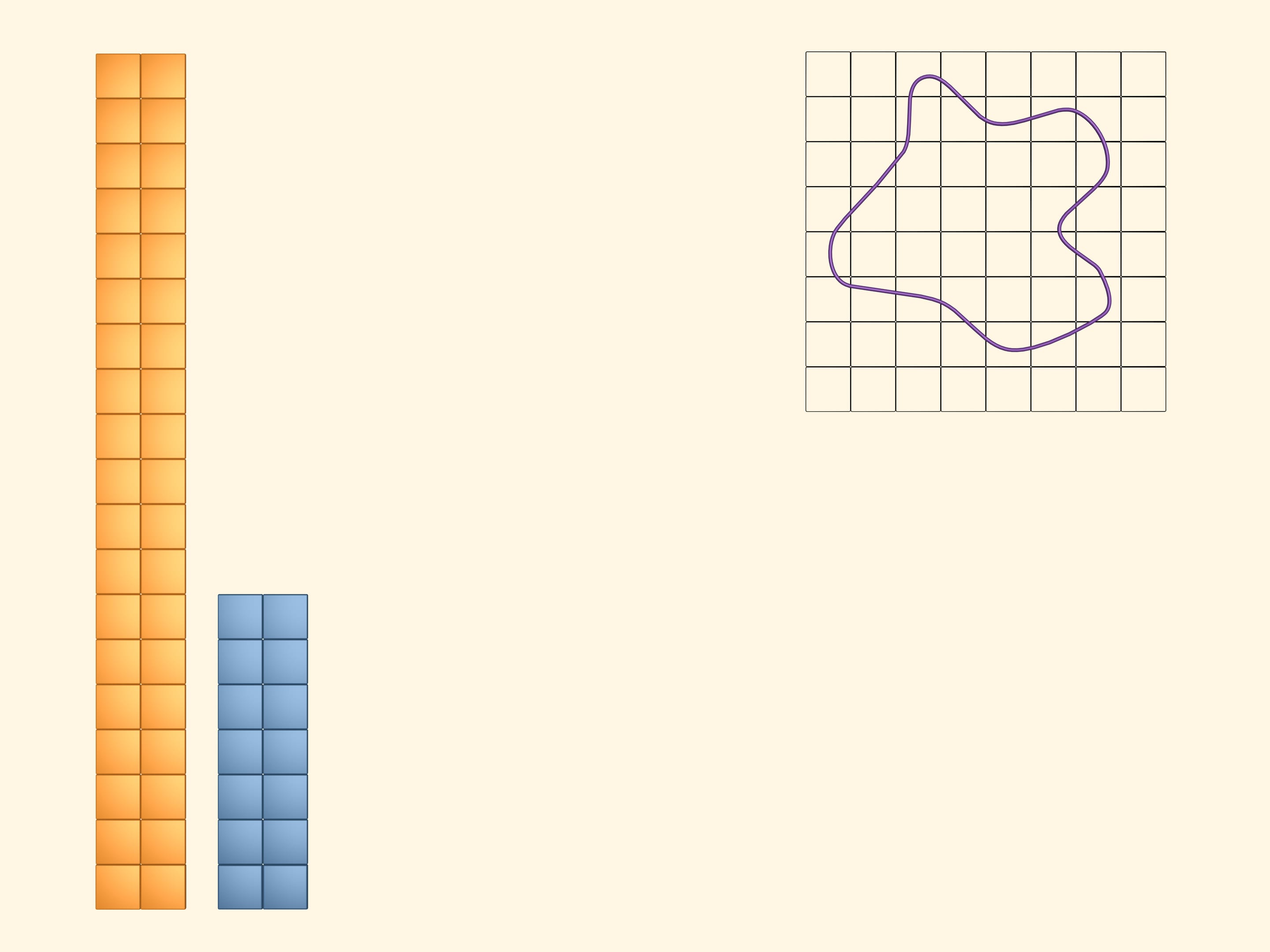
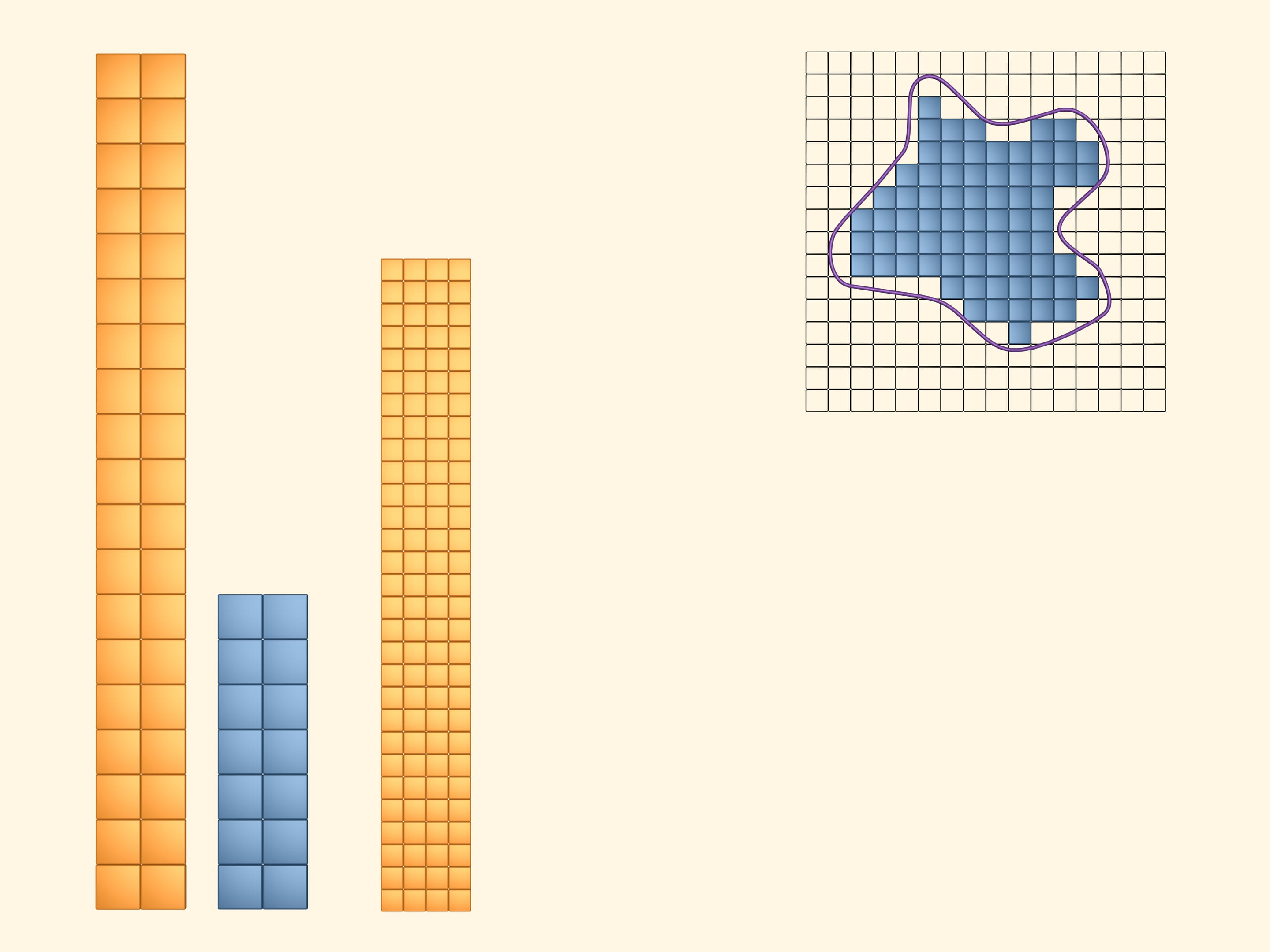
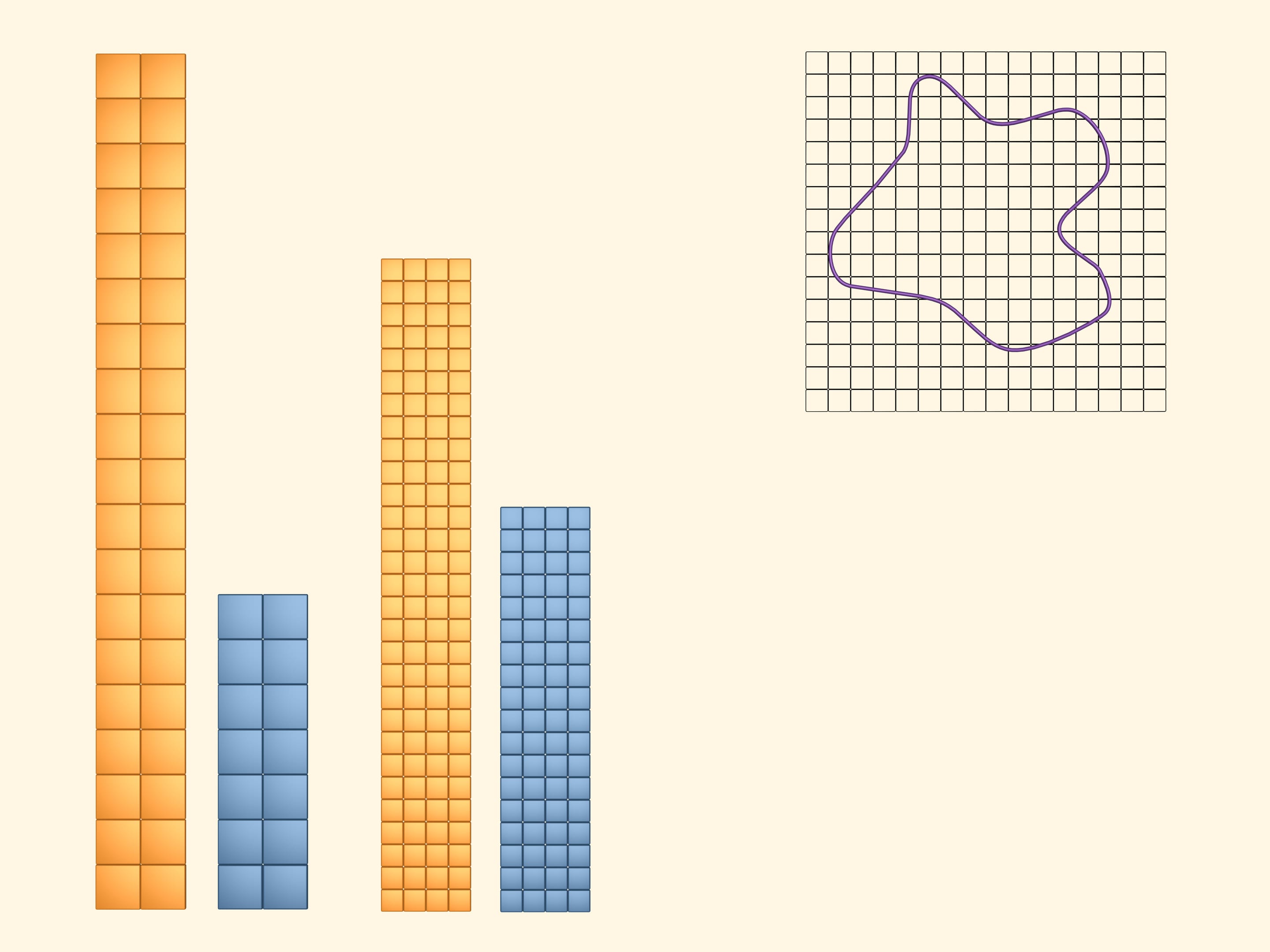
Sovrapponiamo alla figura piana in questione un reticolo quadrato.
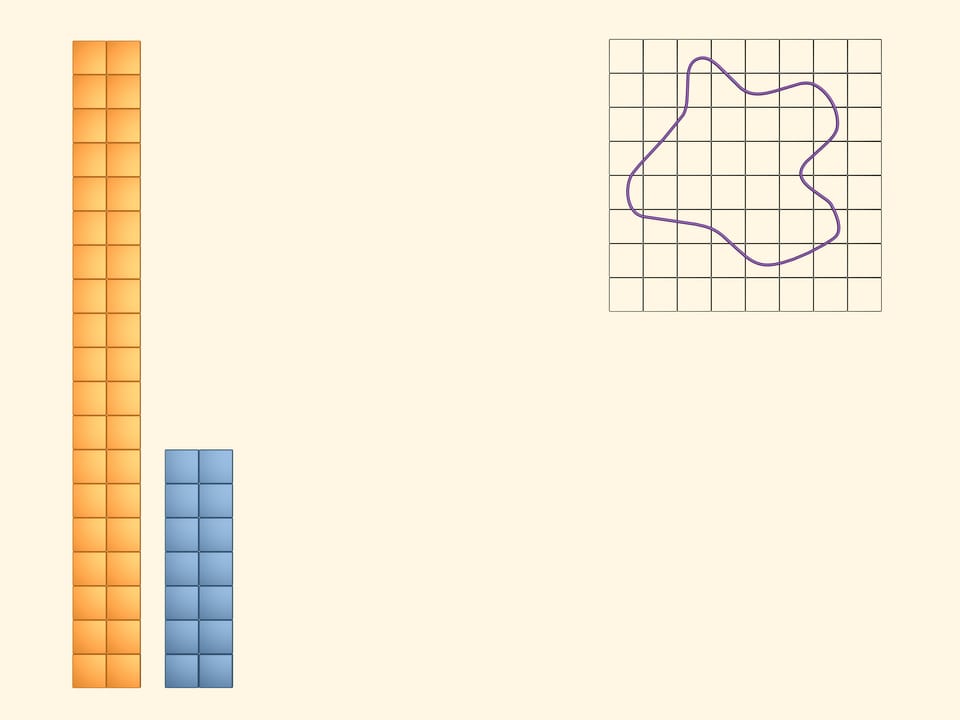
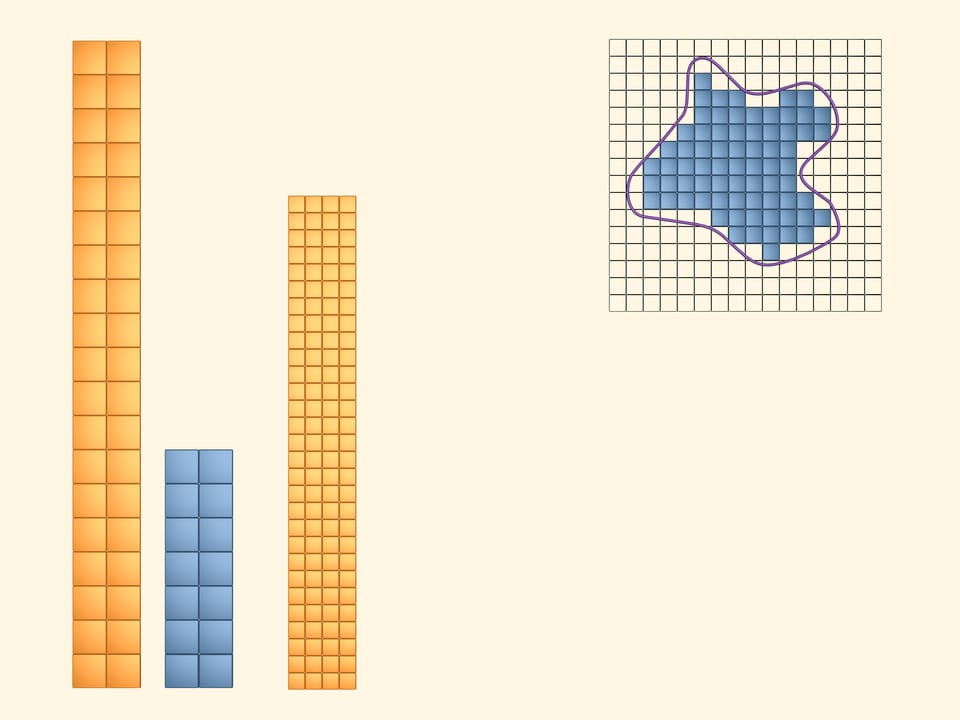
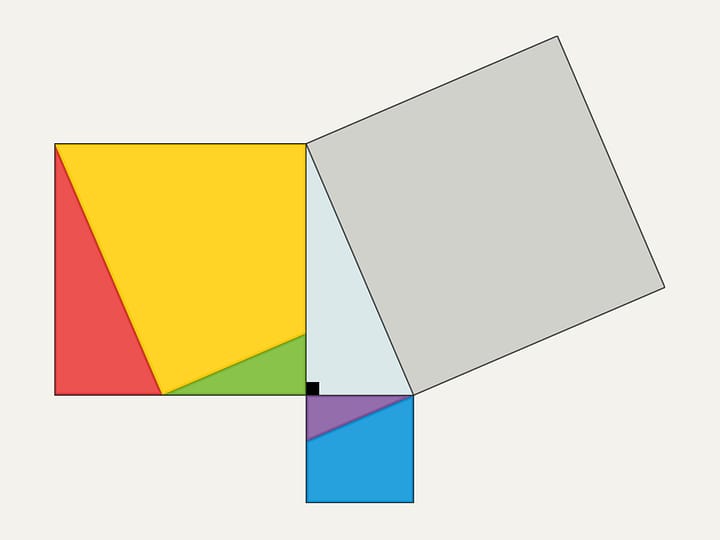
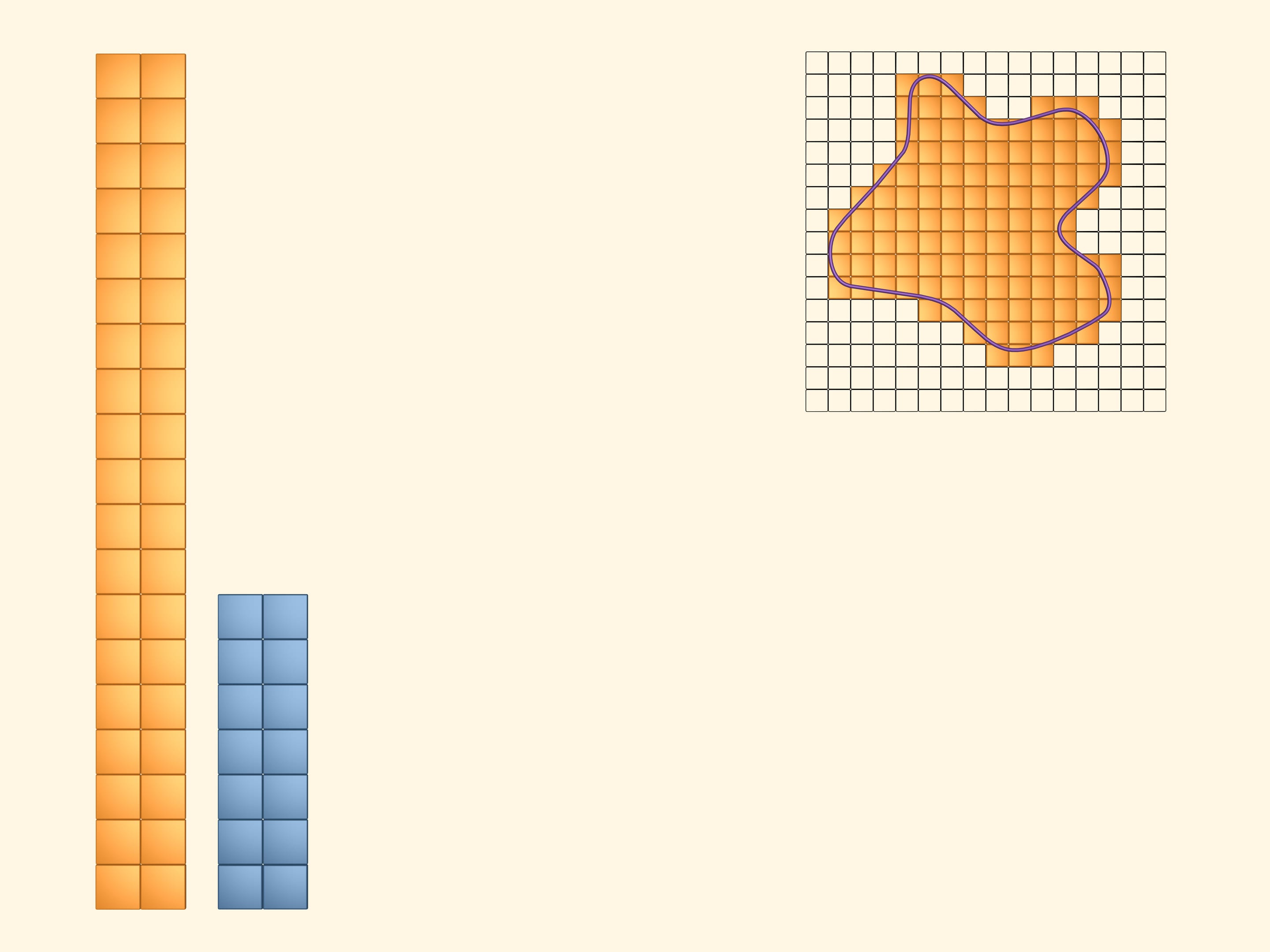
Coloriamo di giallo tutti i quadrati che intersecano almeno in parte la figura. Per visualizzare e calcolare l’area occupata dai quadrati gialli, costruiamo con essi un rettangolo. È evidente che la quantità, che chiameremo area della figura in esame, è inferiore all’area di questo rettangolo giallo.
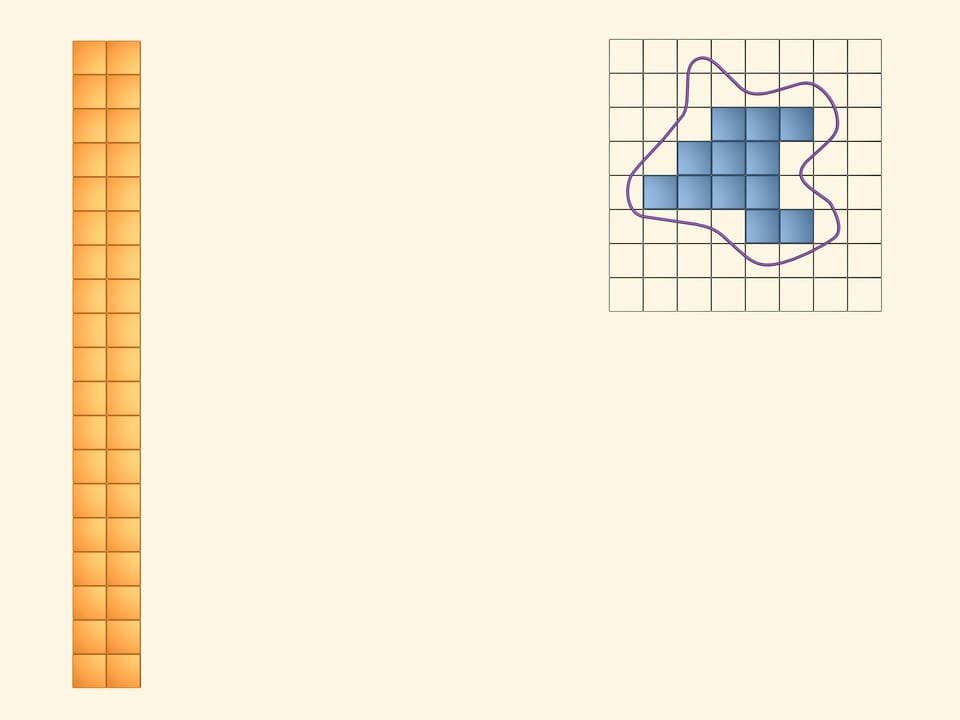
Coloriamo ora di azzurro tutti quei quadrati che si trovano completamente all’interno della nostra figura. Di questi quadrati ce ne sono di meno, ovviamente, di quelli gialli. Anche con questi costruiamo un rettangolo. L’area della nostra figura è superiore all’area di questo rettangolo azzurro.
Sicché quello che noi vorremmo chiamare area della figura in esame è più grande dell’area del rettangolo blu ed è più piccolo di quella del rettangolo giallo. Ma le aree di questi due rettangoli sono parecchio diverse, e per ora non abbiamo dell’area cercata.
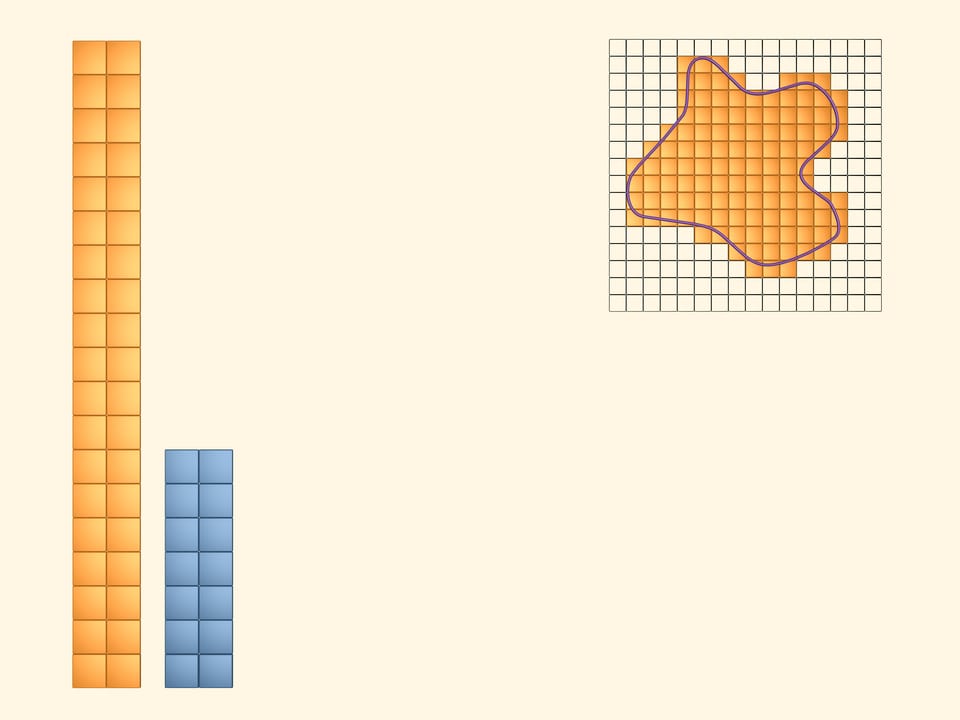
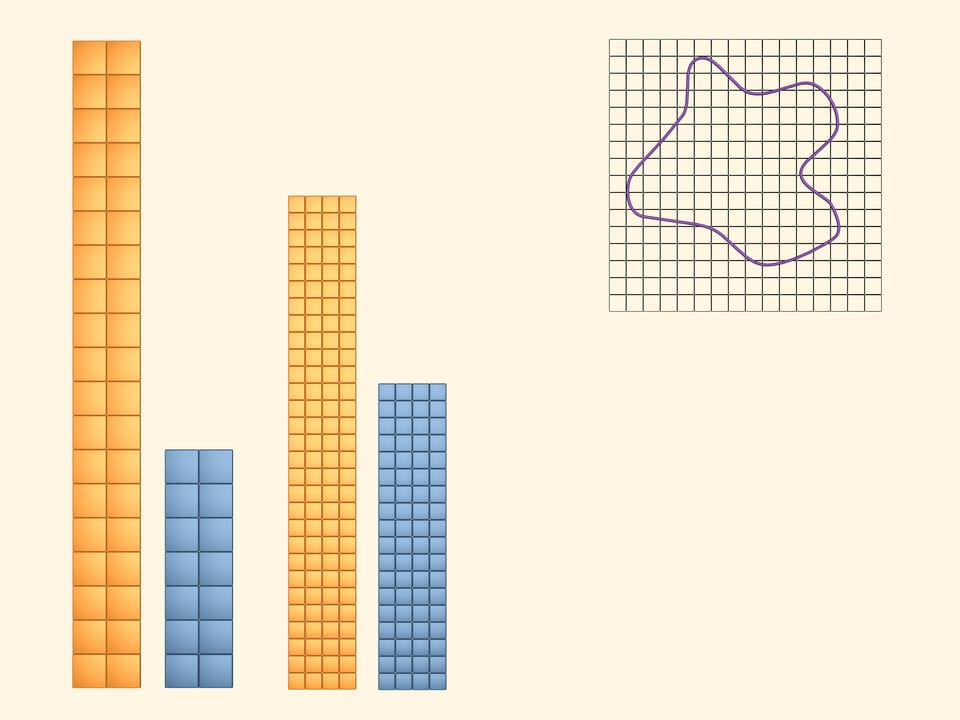
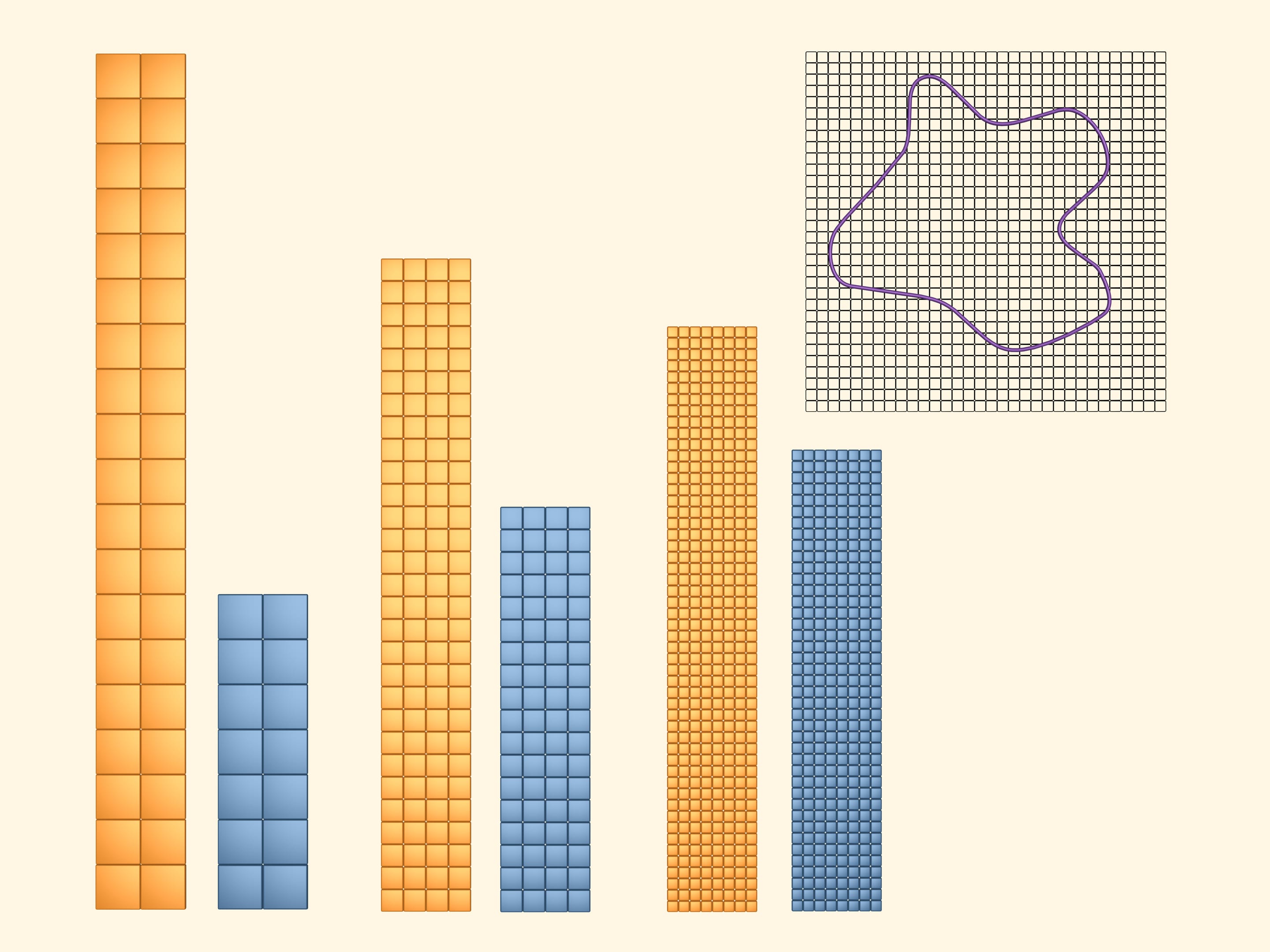
Al fine di ottenere dei limiti inferiore e superiore più accurati per la quantità cercata, consideriamo un reticolo a celle quadrate più piccole. Ripetiamo i passaggi precedenti. Coloriamo in giallo i quadrati che almeno in parte intersecano la figura. E in azzurro coloriamo quelli che stanno interamente dentro la figura. Di nuovo l’area della figura risulta più grande dell’area del rettangolo azzurro e più piccola dell’area del rettangolo giallo. Ma questa volta, avendo preso un reticolo più fine, otteniamo i limiti superiore e inferiore più vicini tra loro.
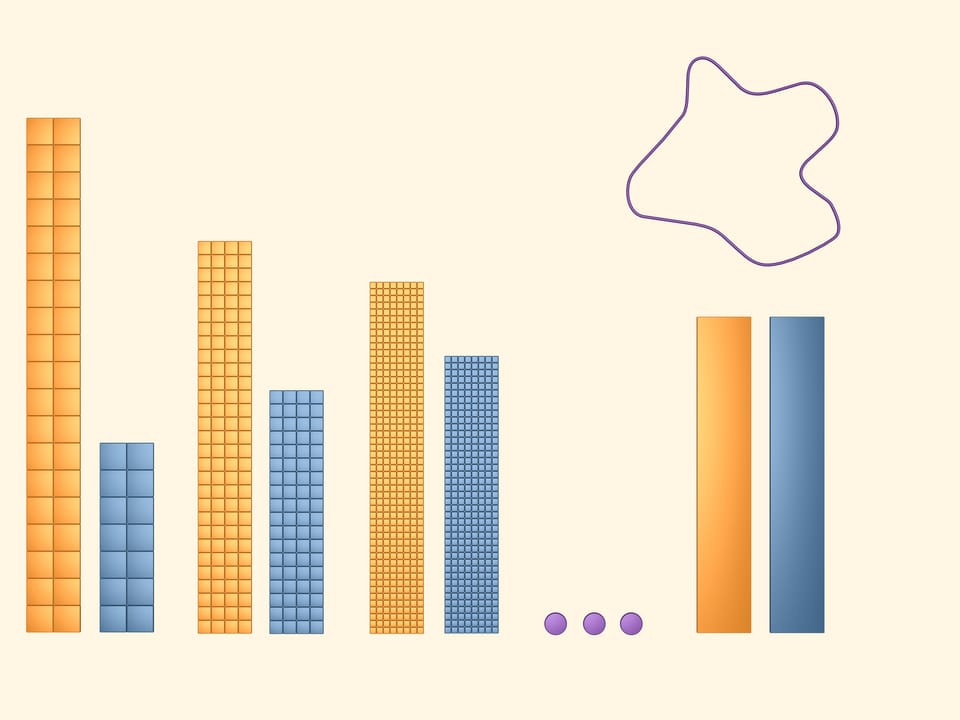
Considerando reticoli sempre più fini, otteniamo dei limiti superiori e inferiori sempre più precisi per l’area cercata.
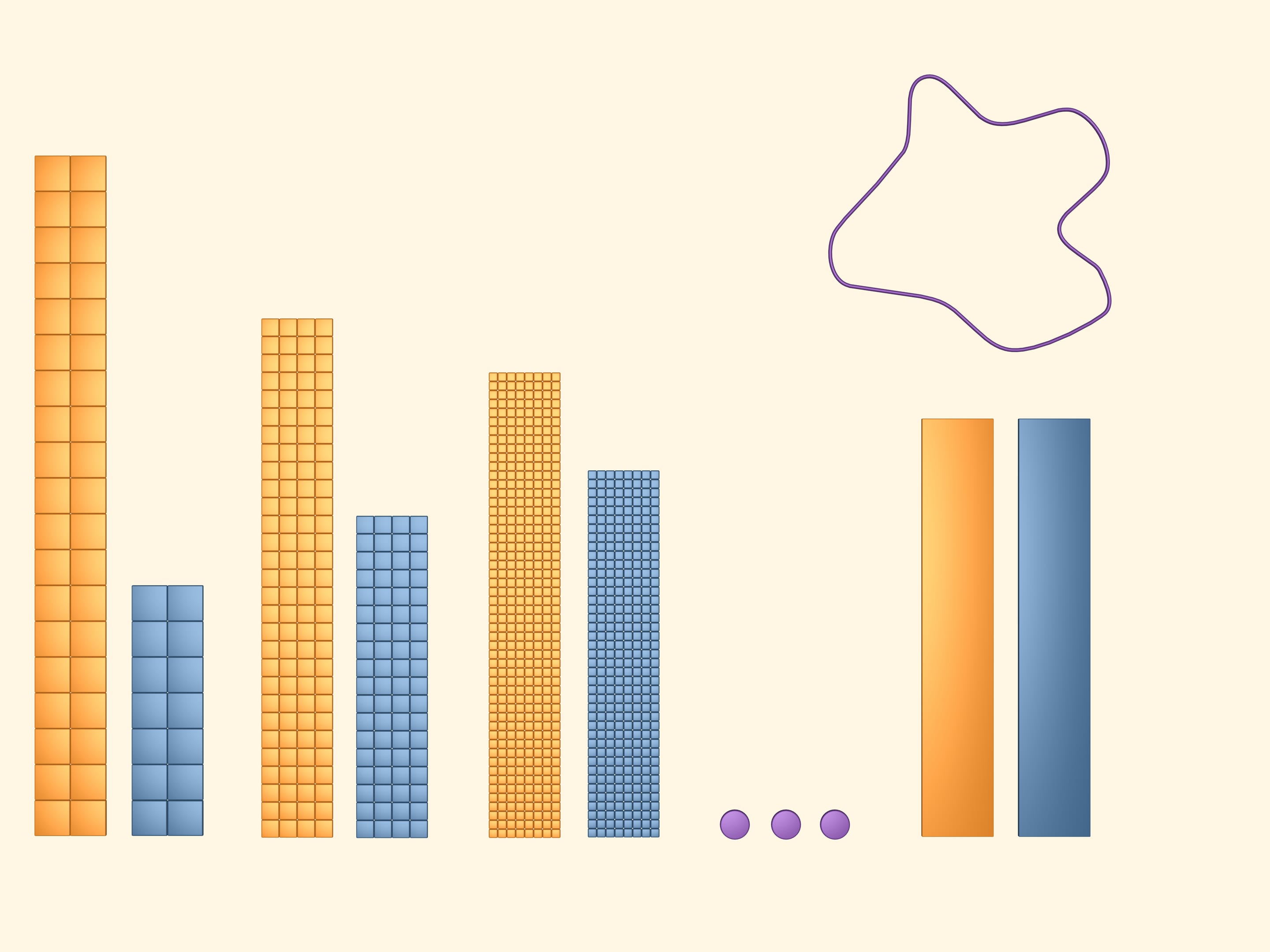
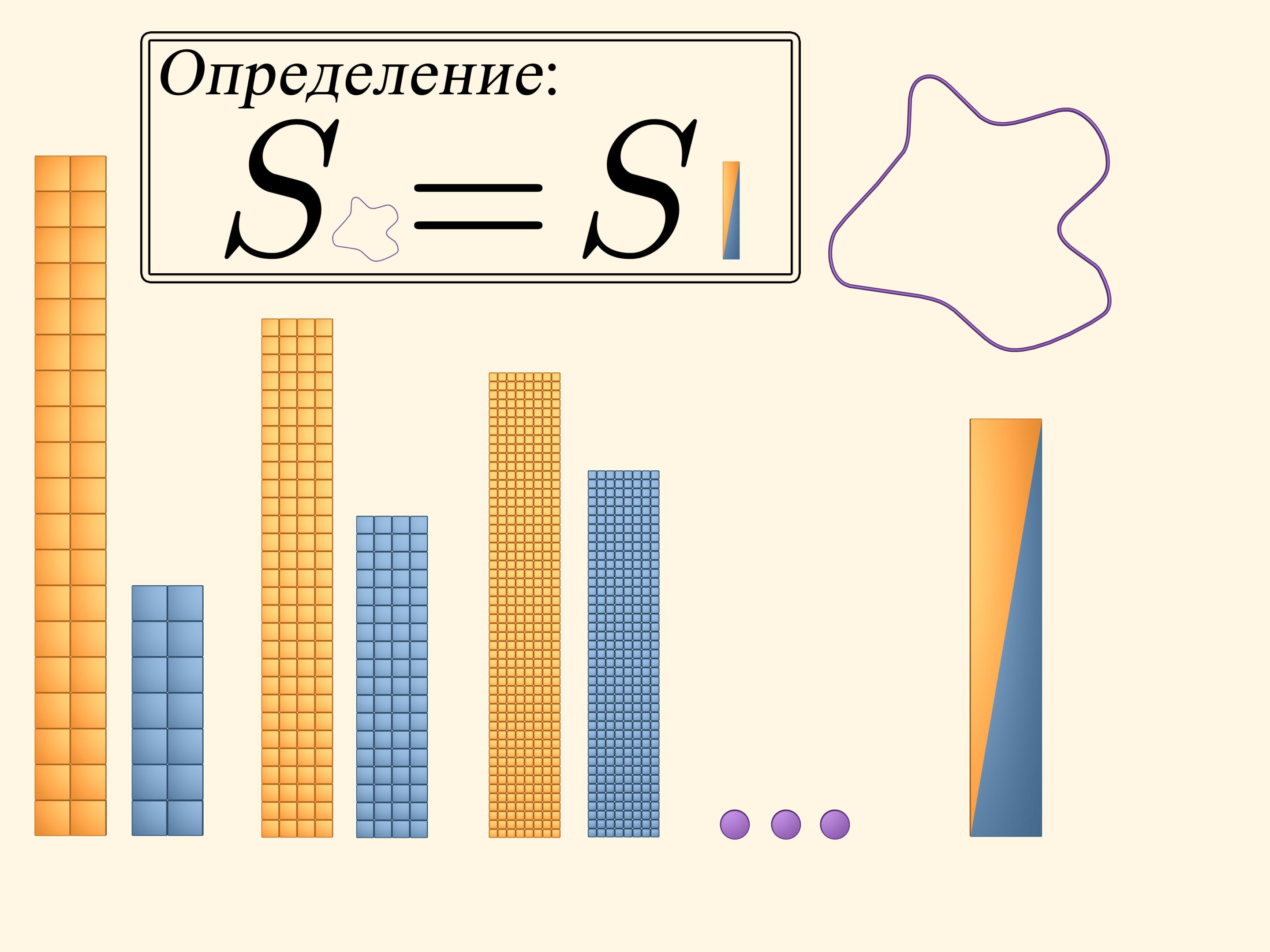
Continuando a raffinare il reticolo, l’area dei quadrati, di cui esso è costituito, tende a zero. Facendo un’astrazione dalla realtà, nel modello matematico si dice che si possono rendere i quadratini tanto piccoli quanto si vuole. Allora, così si dice, al limite il poligono giallo e quello azzurro risulteranno uguali. Consideriamo un rettangolo, fatto delle metà di questi rettangoli giallo e azzurro (si potrebbe anche considerare uno solo di essi).
L’area cercata della figura è per definizione l’area del rettangolo di due colori.
Nella realtà quotidiana esistono casi in cui è sufficiente definire approssimativamente l’area di una figura. L’area calcolata, cioè, deve differire da quella vera di una data quantità al massimo. Per risolvere questo problema è necessario prendere un reticolo di quadratini tale che la differenza tra le aree dei rettangoli giallo e azzurro non superi il doppio del margine di errore definito. Allora come area della figura bisogna prendere un numero pari alla somma delle aree dei rettangoli giallo e azzurro, divisa per due.