Solidi a facce ricurve con lo stesso sviluppo di poliedri

Si può ripiegare lo sviluppo di un poliedro in modo da ottenere un solido, le cui facce non sono piane ma superfici ricurve?

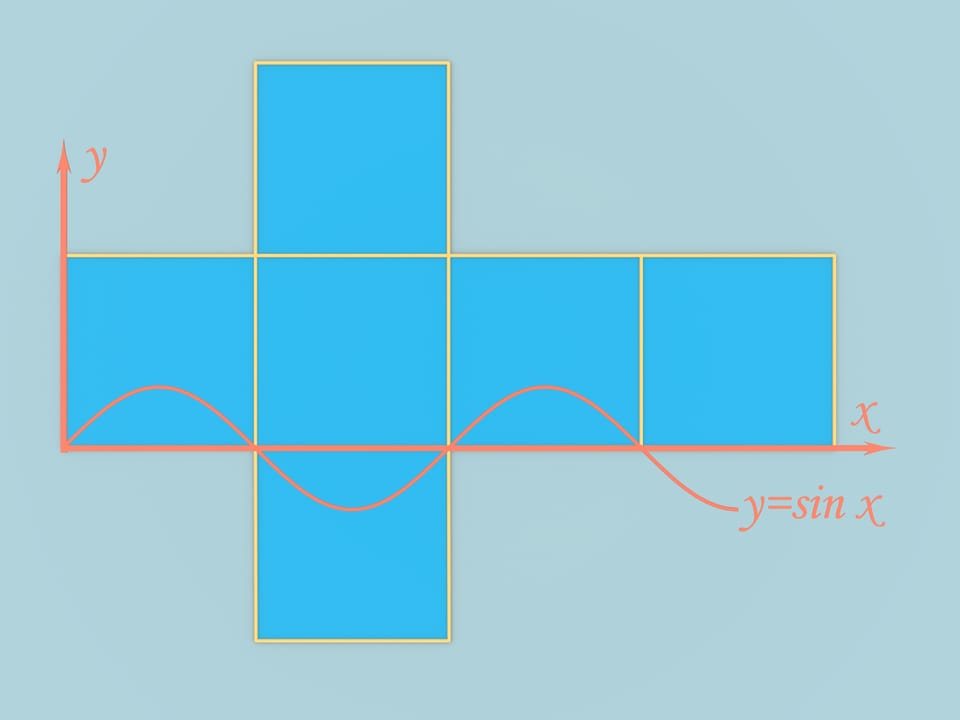
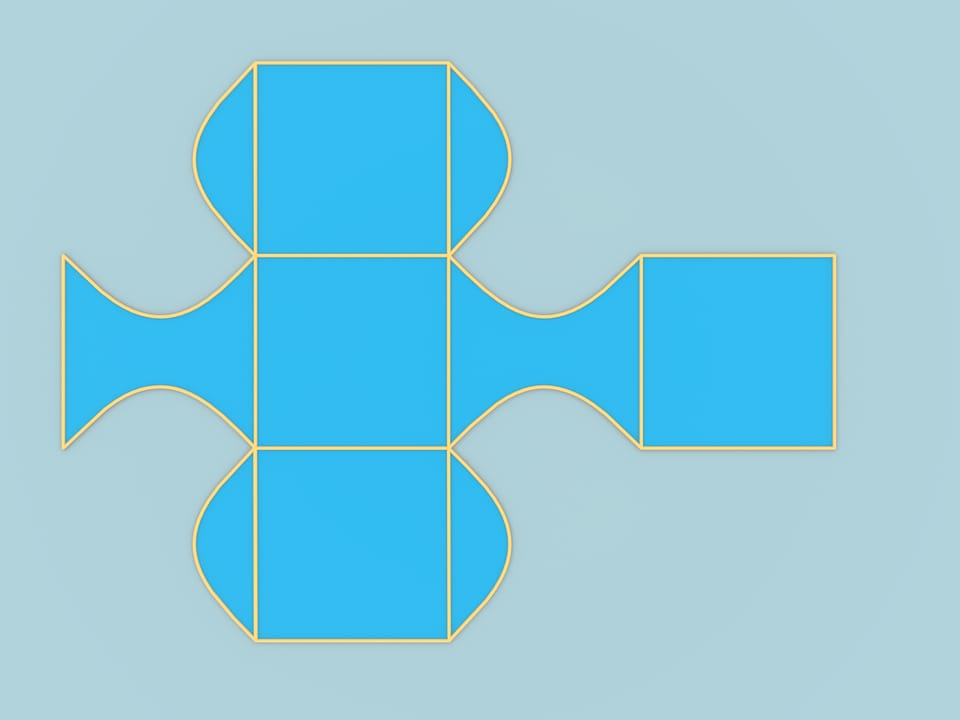
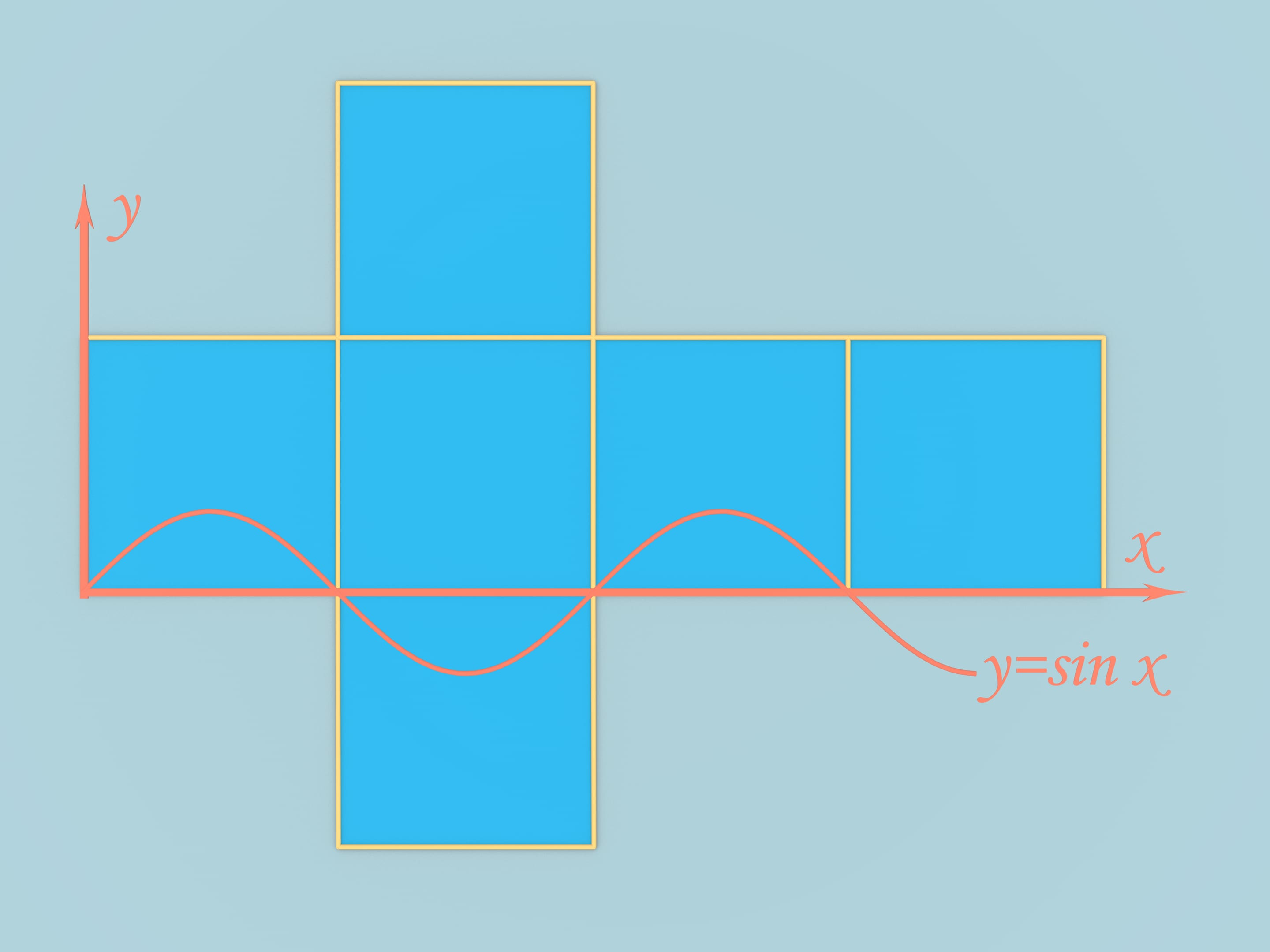
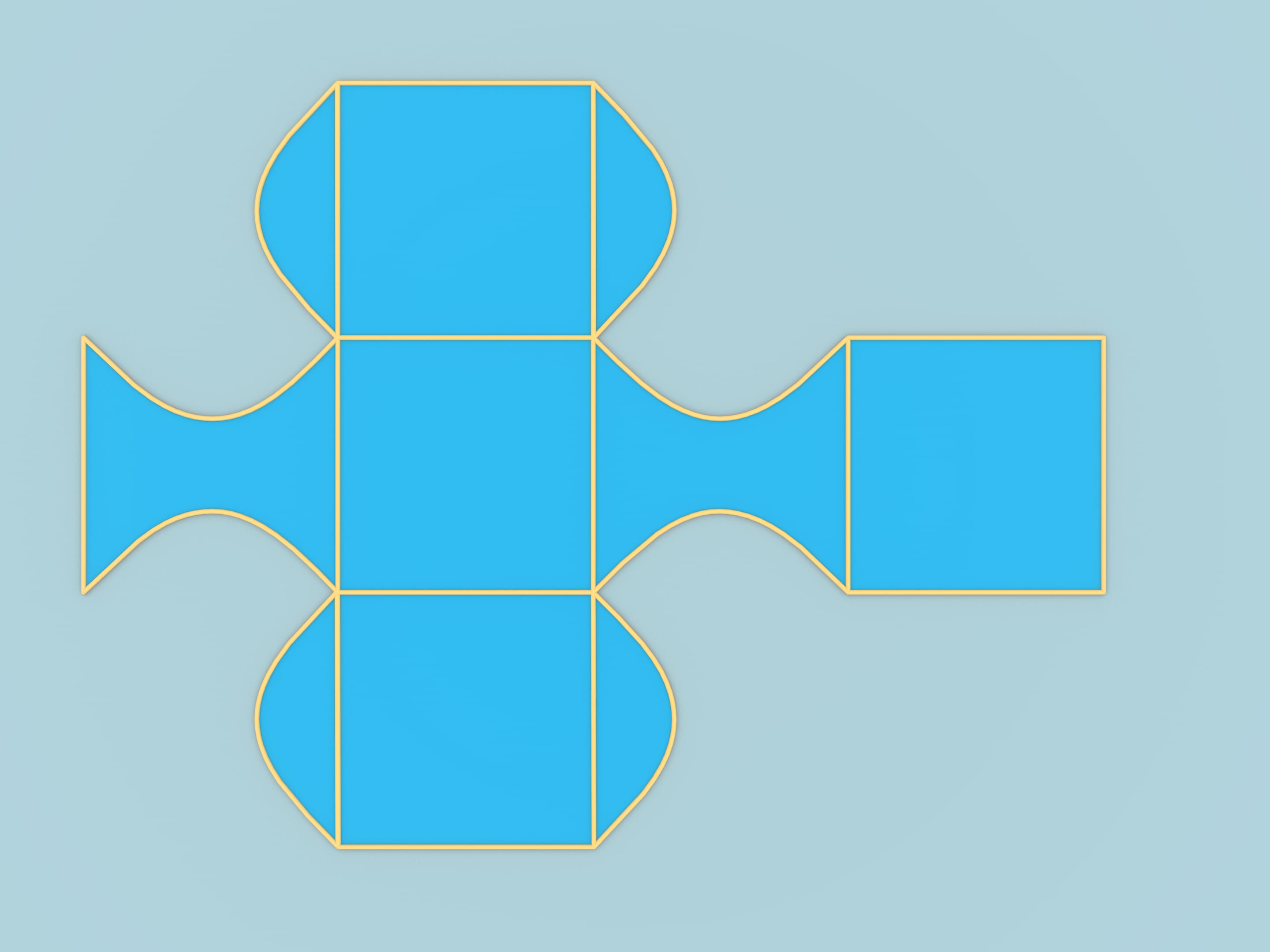
Prendiamo un cubo con spigoli uguali a $\pi$. Distendiamo il suo sviluppo a forma di croce latina su un piano, e tracciamo il grafico della funzione $y=sin(x)$, scegliendo gli assi in modo opportuno. Spostiamo i pezzi tagliati dal grafico e quelli che sono simmetrici ad essi. Lo sviluppo resta lo stesso, in quanto le condizioni di incollamento ai bordi sono state rispettate durante l’operazione. Ma ora lo sviluppo può essere ripiegato ottenendo questo solido.

Ma questo esempio, pur rispondendo alla questione, ha un difetto: in esso restano intatte due facce del cubo, che sono superfici piane. In seguito alla costruzione di questo esempio, ne fu presto trovato un altro, che non aveva quel difetto.

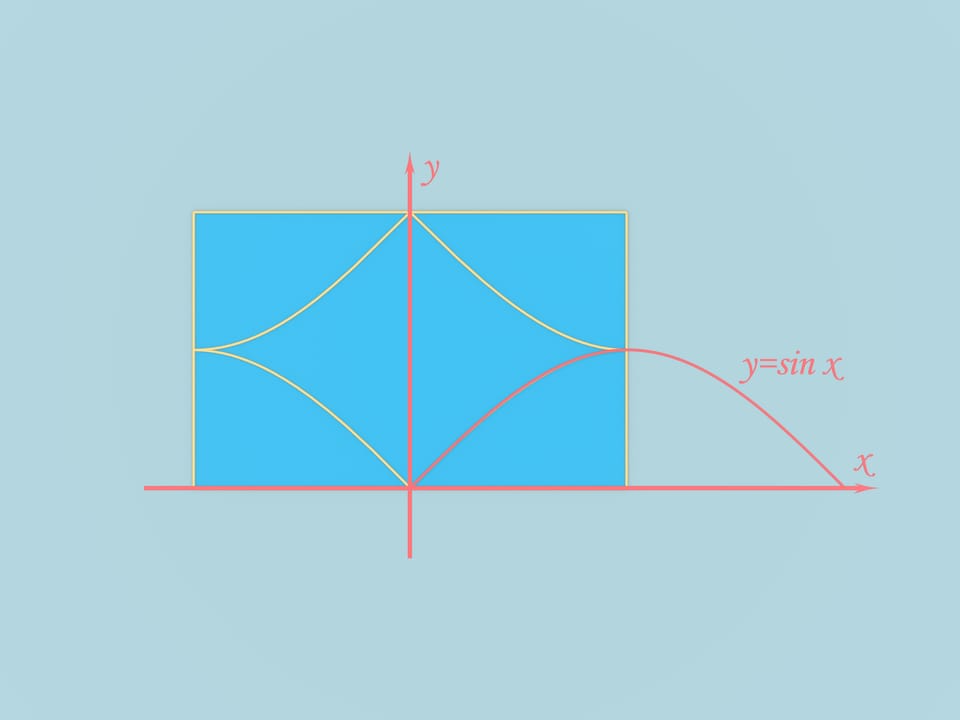
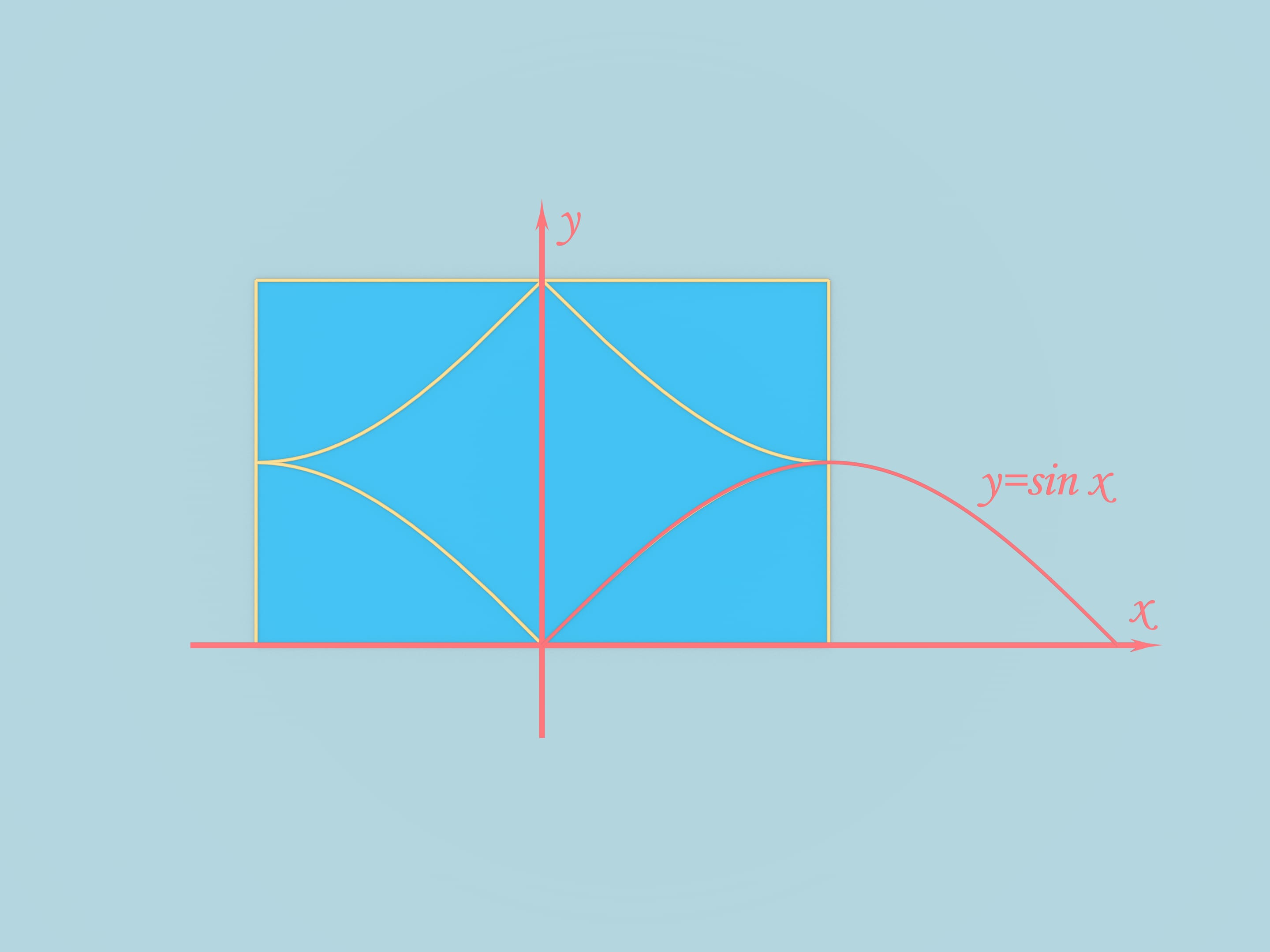
Prendiamo un foglio di carta rettangolare i cui lati stanno nella proporzione $\pi/2$. Da esso, come da qualsiasi rettangolo, si può ottenere una piramide a base triangolare, nel modo seguente. Tracciamo degli spigoli unendo tra loro i punti medi dei lati adiacenti del rettangolo, e in più tracciamo uno spigolo, che unisce i punti medi dei lati più lunghi. Ripiegando il foglio lungo questi spigoli, otteniamo una piramide.

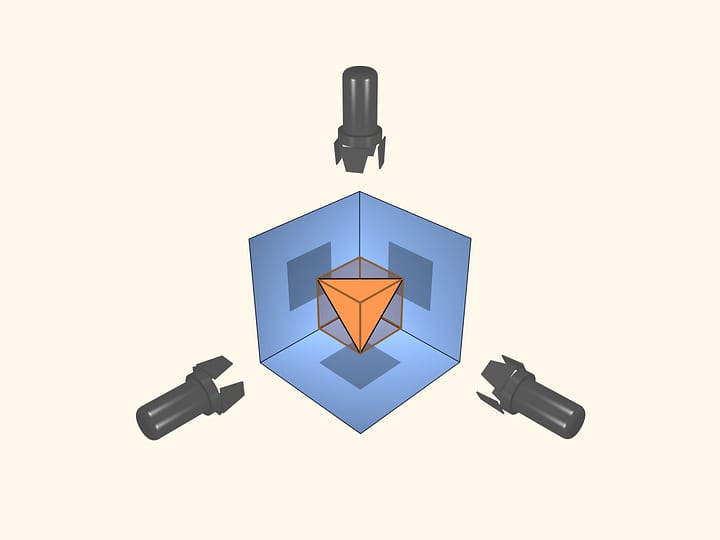
Ma dallo stesso foglio di carta possiamo ottenere anche un altro solido, la cui superficie è fatta di superfici ricurve. Uniamo i punti medi dei lati adiacenti del rettangolo con dei “quarti” di sinusoide. Pieghiamo il foglio lungo questi spigoli. Ecco che solido interes­sante otteniamo. Esso risulta dall’intersezione di tre cilindri: due di essi sono tangenti tra loro e il terzo è perpendicolare ai primi due. La superficie del nostro solido consiste perciò di tre pezzi di cilindro.

È sorprendente quanto sia giovane questa matematica. Potrebbe sembrare che questi esempi avrebbero potuto costruirli anche se non al tempo di Archimede, comunque molto tempo fa. Invece, gli esempi che abbiamo mostrato furono costruiti soltanto dell’autunno 2004.