Lo sviluppo⁠

Che cos’è lo sviluppo di un poliedro? – vi chiederete. È semplicemente un pezzo di cartone ripiegando il quale si costruisce il poliedro dato. Questo è vero, ma c’è dell’altro. Il concetto di sviluppo di un poliedro racchiude in sé qualcosa di più di un semplice pezzo di cartone.

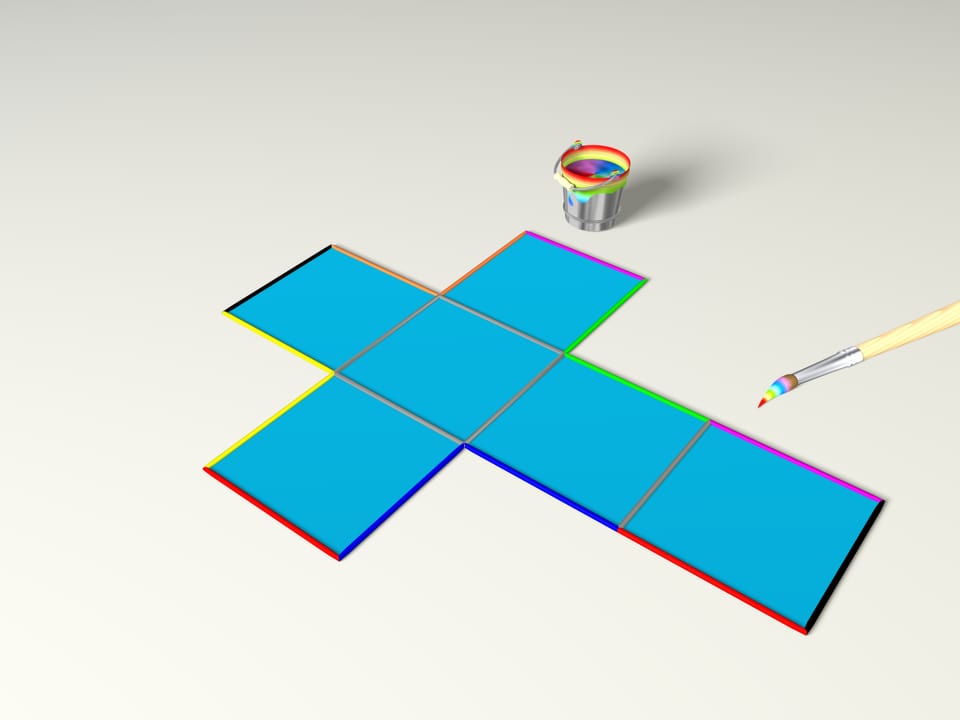
Quale poliedro si può ottenere ripiegando la ben nota croce latina? Il cubo, ovviamente. Per questo bisogna colorare gli spigoli, come ha fatto il nostro pennello magico (gli spigoli dello stesso colore si attaccano l’uno all’altro nel poliedro).

Tuttavia, sarebbe meglio colorare con diversi colori non gli spigoli, ma ogni coppia di punti. Questo corrisponderebbe a dare, come viene detto in matematica, le condizioni di incollamento dei bordi.

Dopo che sono state date le condizioni di incollamento dei bordi, gli spigoli situati dentro il pezzo di cartone sono definiti univocamente, secondo un teorema di A.D. Aleksandrov.

Sicché dalla croce si può ottenere un cubo.

Ma avviene che se le condizioni di incollamento sono date diversamente, si può ottenere tutt’altro che un cubo!

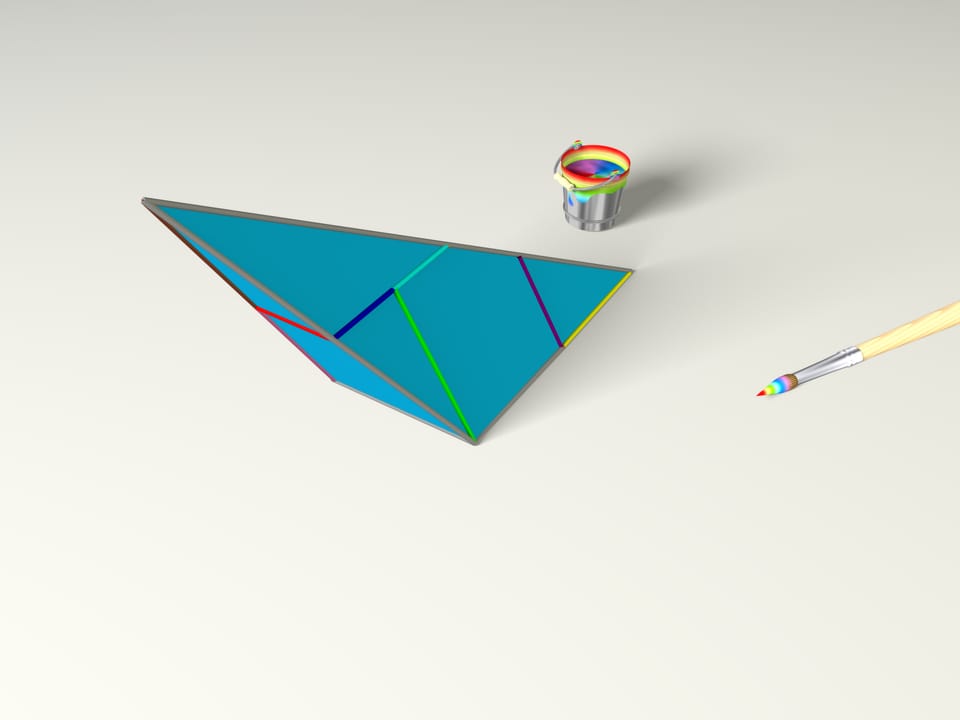
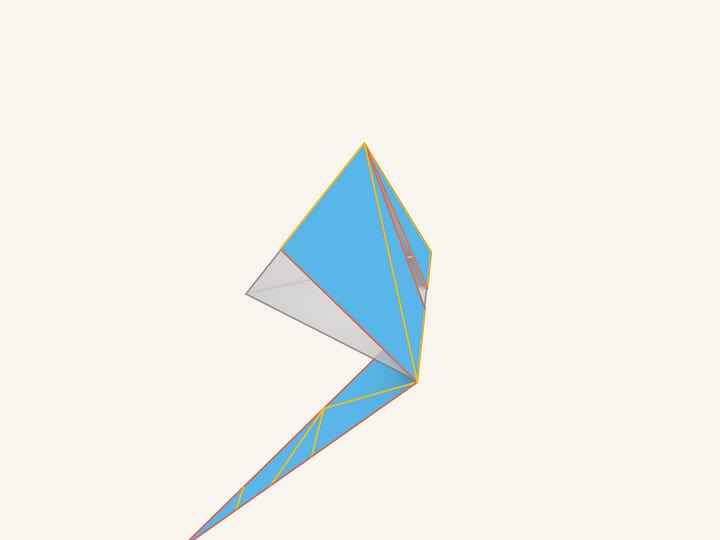
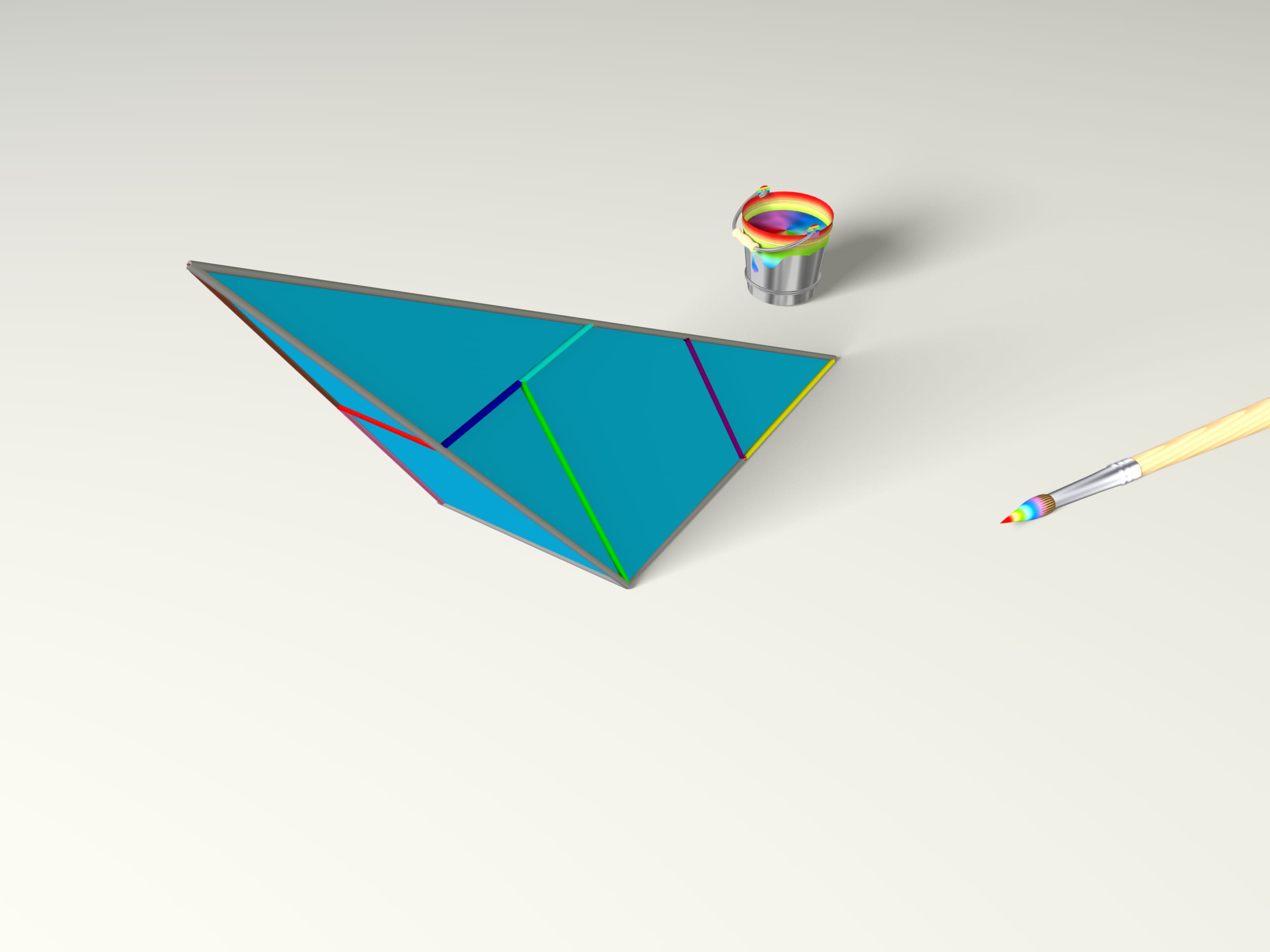
Il nostro pennello magico ha colorato i bordi ecco in che modo. Un’ultima pennellata delle sue e già sappiamo definire gli spigoli all’interno del pezzo di cartone. Se ora costruiamo un poliedro, seguendo le condizioni di incollamento appena disegnate, otteniamo una piramide!

Non molto tempo fa è stato dimostrato che dando diverse condizioni di incollamento dei bordi della croce latina, si possono ottenere 5 tipi diversi di poliedri convessi.

Dunque, come abbiamo visto, il concetto di sviluppo di un poliedro non consiste solo un pezzo di cartone, ma anche nelle condizioni di incollamento dei bordi. Se queste non sono definite, allora dallo stesso pezzo di cartone si possono ottenere diversi poliedri convessi.