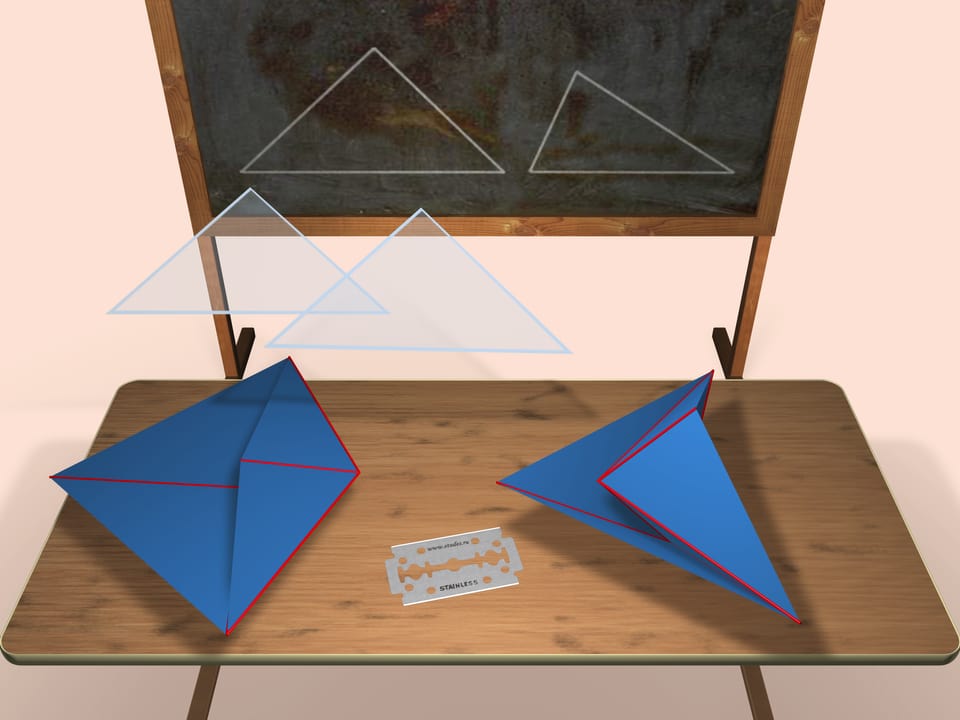
È possibile costruire dallo stesso insieme di facce sia un poliedro convesso sia uno non convesso? Vedremo che la risposta è sì. Un esempio è mostrato in figura.
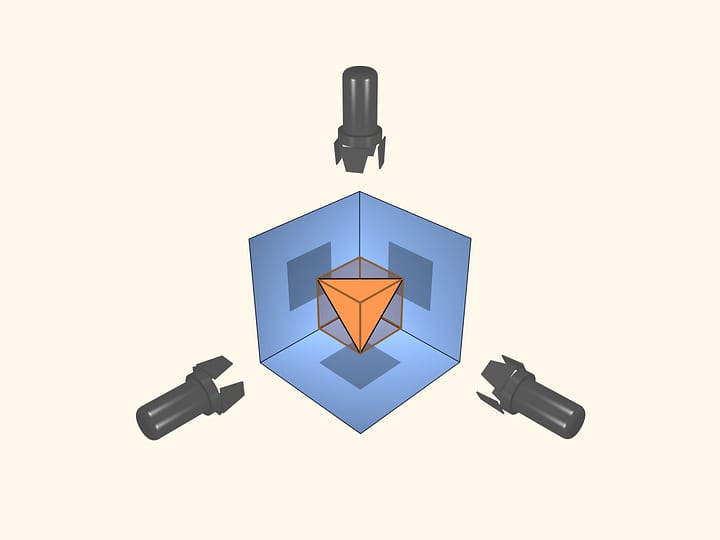
Un poliedro è detto convesso se è situato in un singolo semi–spazio rispetto a qualsiasi piano contenente una delle sue facce.
Un poliedro è non convesso se esiste un piano contenente una delle sue facce che lo interseca.
Supponiamo di aver costruito un poliedro convesso e un altro non convesso dallo stesso insieme di facce. Quale di essi ha il volume più grande?
Scopriremo ora che possiamo scegliere le facce, in modo che il volume del poliedro non convesso sia maggiore del volume del poliedro convesso che ha le stesse facce. Questo film vi mostra l’esempio finora più noto.
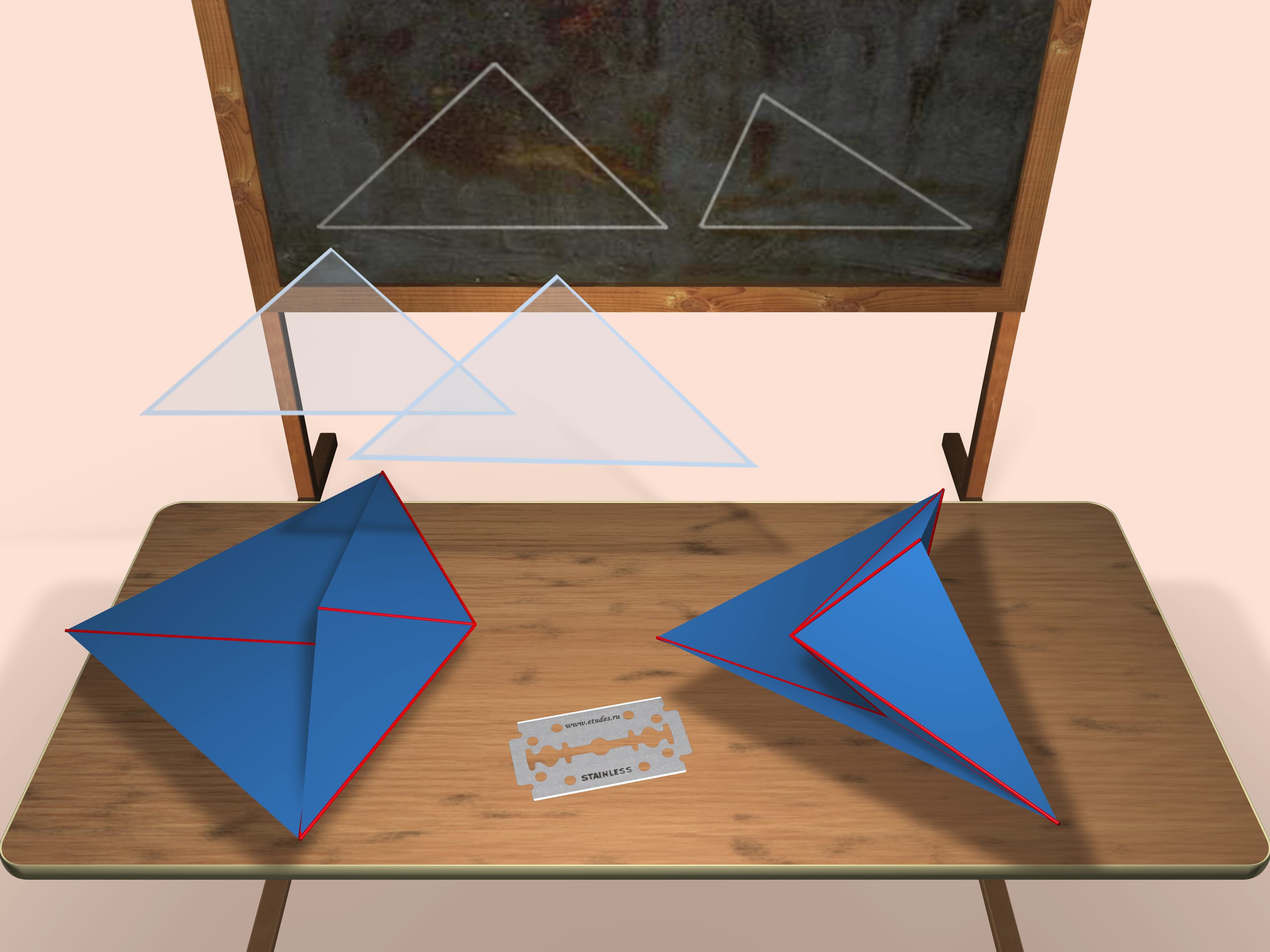
Consideriamo due triangoli (la lunghezza precisa del loro lati verrà data alla fine del film) che saranno uguali alle facce di entrambi i nostri poliedri. Quello mostrato a sinistra è convesso, quello mostrato a destra non lo è.
Entrambi i poliedri che abbiamo costruito sono ottaedri (irregolari) ossia essi hanno otto facce e sei vertici.
Qual è il significato di volume, in particolare, di un poliedro? È la quantità di liquido che si può versare dentro di esso. Tagliamo un vertice a entrambi i poliedri e iniziamo a riempirli con acqua. Quando il poliedro convesso è già riempito, quello non convesso non lo è ancora. Ma forse la velocità dell’acqua era diversa: per misurare la quantità di acqua correttamente, cerchiamo di versare l’acqua da ogni poliedro in due bicchieri identici. Il livello dell’acqua nel bicchiere a destra è superiore di quello a sinistra. Ciò significa che il volume del poliedro non convesso è realmente superiore al volume di quello convesso.
Se si calcola con precisione si otterrà che il rapporto tra il volume del poliedro non convesso e il volume di quello convesso è 1,163.
Nel nostro problema è più corretto considerare il rapporto tra volumi che la loro differenza, in quanto il rapporto non dipende dalla dimensione dei triangoli iniziali usati per costruire i poliedri.
Il volume del poliedro non convesso è più del 16% superiore a quello del poliedro convesso. Potete costruirvi questi poliedri da soli usando delle facce con i lati delle lunghezze mostrate. Se avete posto i centri degli ottaedri nell’origine delle coordinate, i vertici avranno le stesse coordinate, come mostrato nel film.
L’esempio che abbiamo mostrato fu costruito da S.N. Mikhalev mentre svolgeva il dottorato di ricerca All’Università Statale di Mosca . Esso costituisce l’esempio più noto finora (che ha il maggior rapporto tra i volumi dei poliedri).
Tuttavia, non è ancora noto quanto grande può essere il rapporto tra il volume di un poliedro non convesso e quello di uno convesso, costituiti entrambi dello stesso insieme di facce. E questo problema è in attesa del suo risolutore!