Intrappolare i raggi di luce⁠

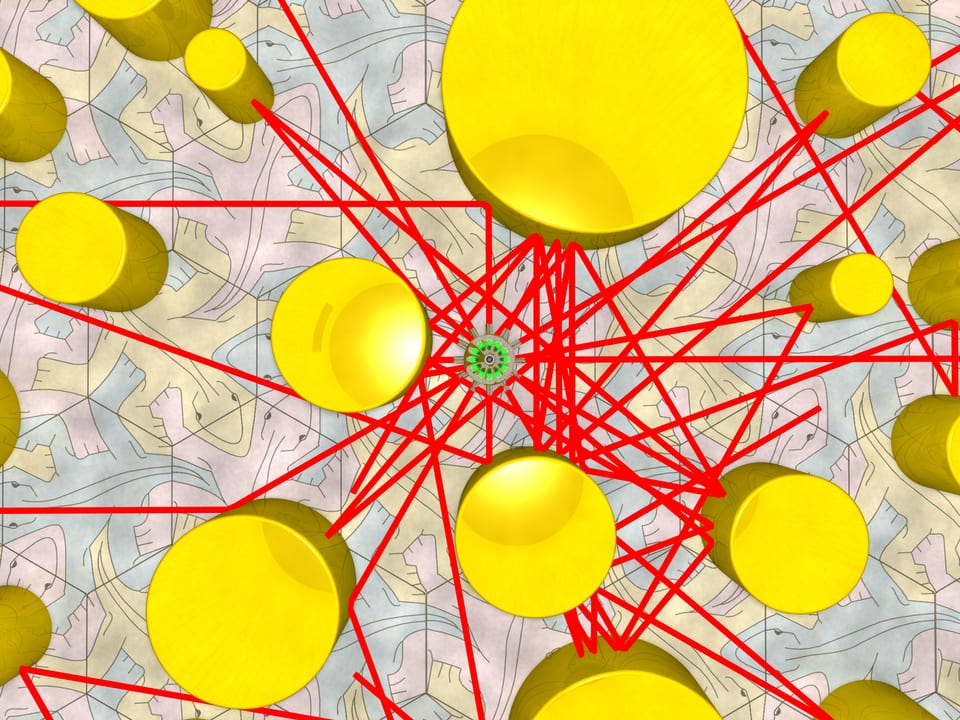
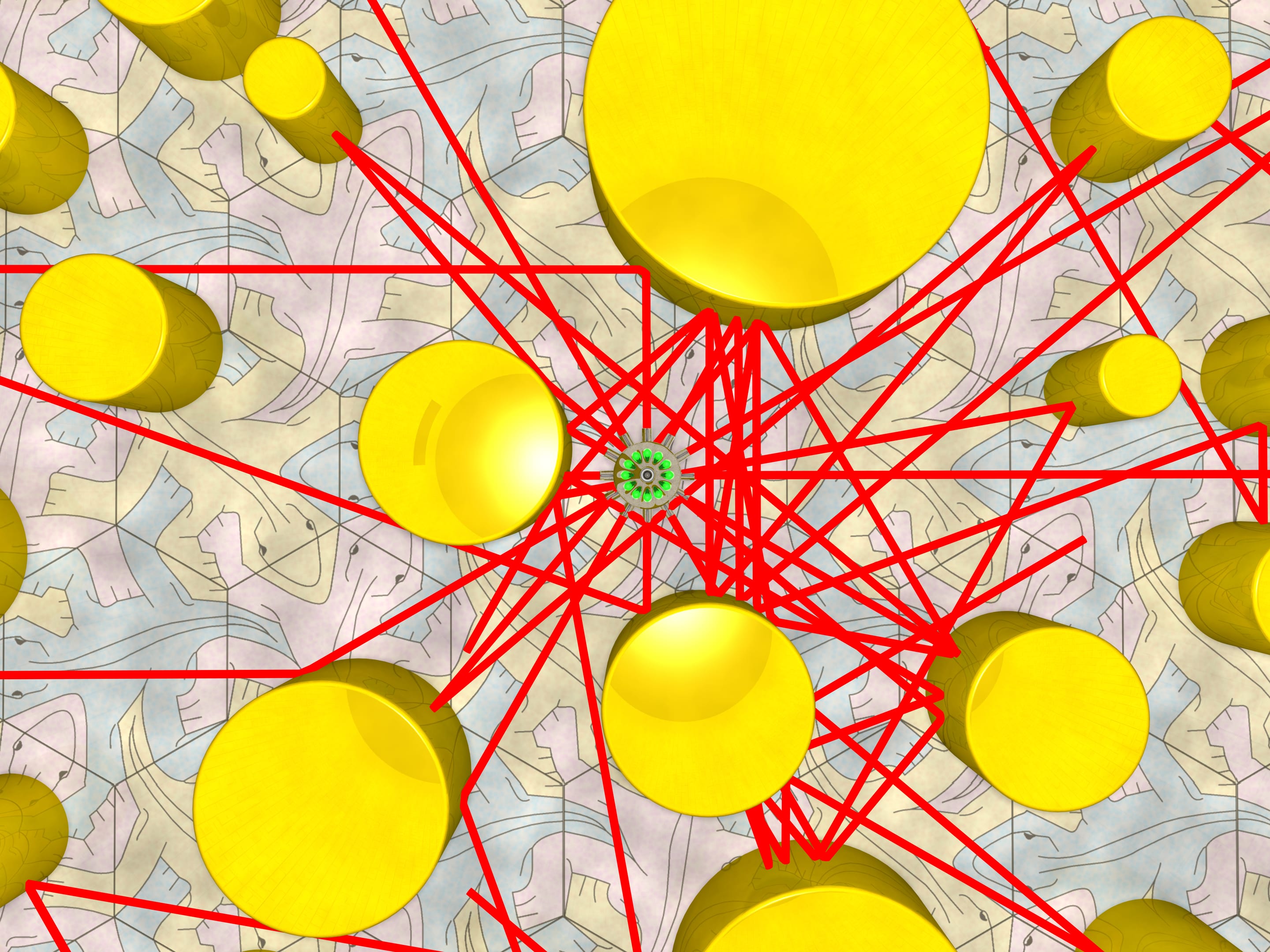
È possibile disporre sul pavimento di una stanza delle colonne cilindriche riflettenti, in modo che un raggio di luce, che si propaga dal centro parallelo al pavimento, non raggiunga mai le pareti? Le colonne con una superficie cilindrica riflettente possono avere diametri arbitrari e essere poste a distanze arbitrarie, a condizione che non si tocchino tra loro (nel qual caso il problema sarebbe banale).

Come è noto, la rifles­sione da uno specchio avviene secondo la legge che “l’angolo di incidenza è uguale all’angolo di rifles­sione”. Quando lo specchio non è piano, l’angolo tra il raggio e la superficie dello specchio è l’angolo tra il raggio e il piano tangente alla superficie nel punto di incidenza.

Quante colonne sono neces­sarie e quale deve essere la loro disposizione della stanza, affinché un raggio rimanga intrappolato e non raggiunga le pareti? È sufficiente un numero finito di specchi oppure ce ne vogliono infiniti? Oppure anche un numero infinito non basta?

È evidente che una sola colonna non basta. Il raggio può semplicemente evitarla, ma anche se incide su di essa, dopo la rifles­sione finirà lo stesso sulla parete. In questo modo, un raggio di luce, qualsiasi sia la sua direzione iniziale, finirà sulla parete.

Si capisce anche che due o tre colonne non sono sufficienti: dal centro della stanza le pareti saranno visibili in qualche direzione. Ciò significa che dei raggi, sparati in queste direzioni, raggiungeranno le pareti.

L’intuizione ci dice ancora, e l’esperimento conferma, che una piccola quantità di colonne non è sufficiente per catturare un raggio.

Ma ora mettiamo tante colonne e mandiamo dei raggi “in tutte” le direzioni. L’esperimento mostra che i raggi raggiungono le pareti.

Un esperimento tuttavia non è una dimostrazione. Può essere che bisognava disporre le colonne un po’ diversamente oppure prendere un po’ più di colonne… Finora i matematici non sanno se è sufficiente un numero finito di colonne (sia pure molto grande) per catturare un raggio. Ma se è sufficiente, allora quali devono essere i diametri e le posizioni delle colonne? Ma forse anche un numero infinito di colonne non è sufficiente a risolvere il problema posto?

Forse sarete prprio voi a scoprire come bisogna disporre le colonne?