Il triangolo curvo di Reuleaux⁠

Questa animazione mostra come un concetto geometrico, studiato in ambienti matematici, viene utilizzato nella nostra vita quotidiana.

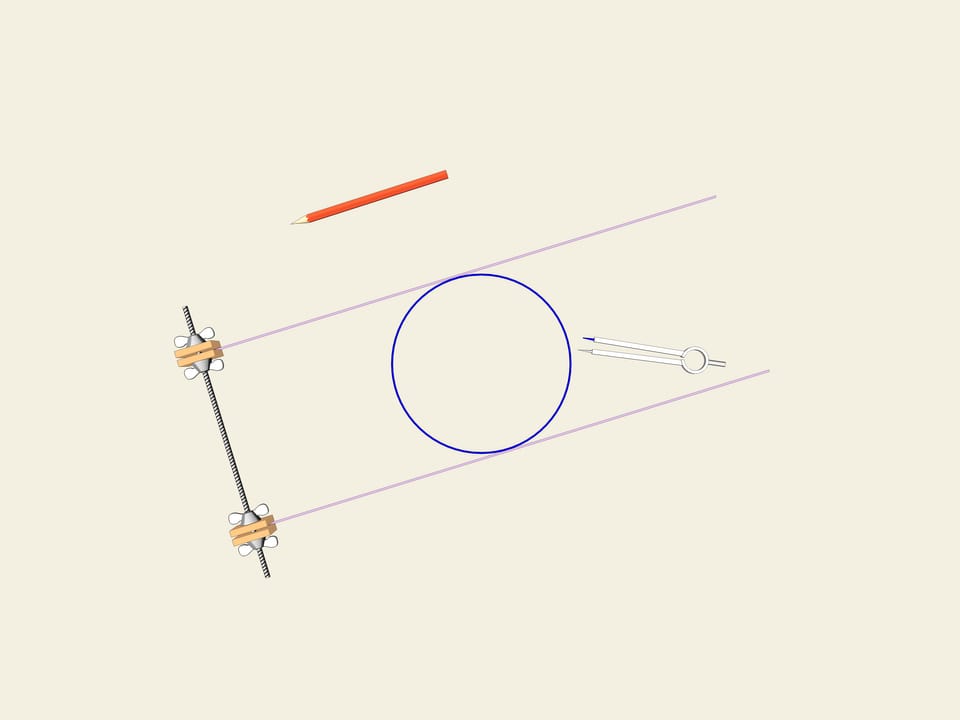
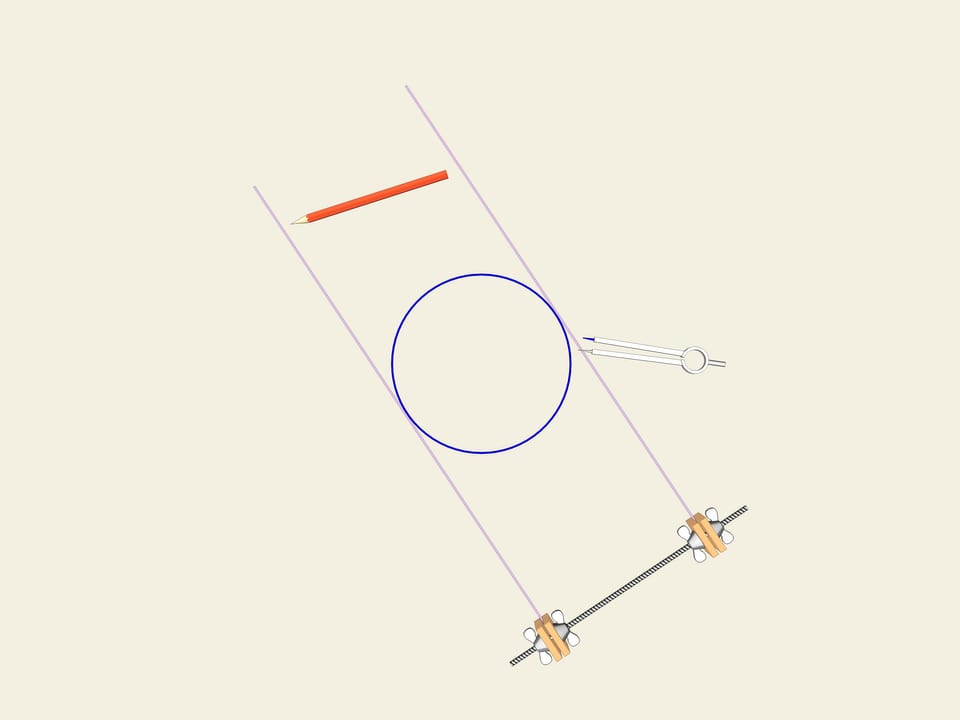
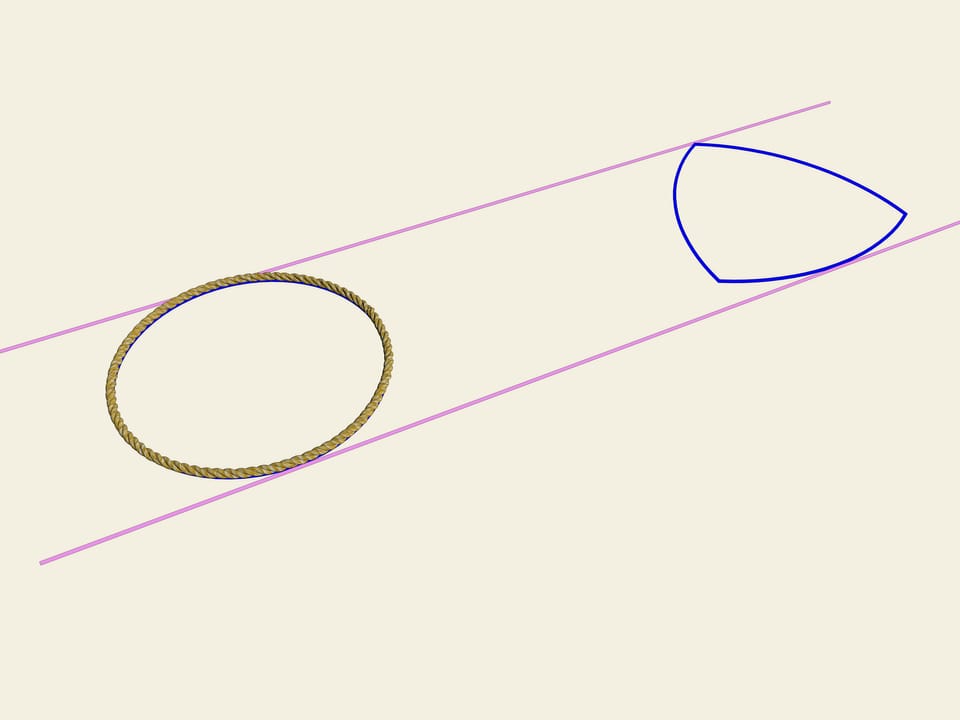
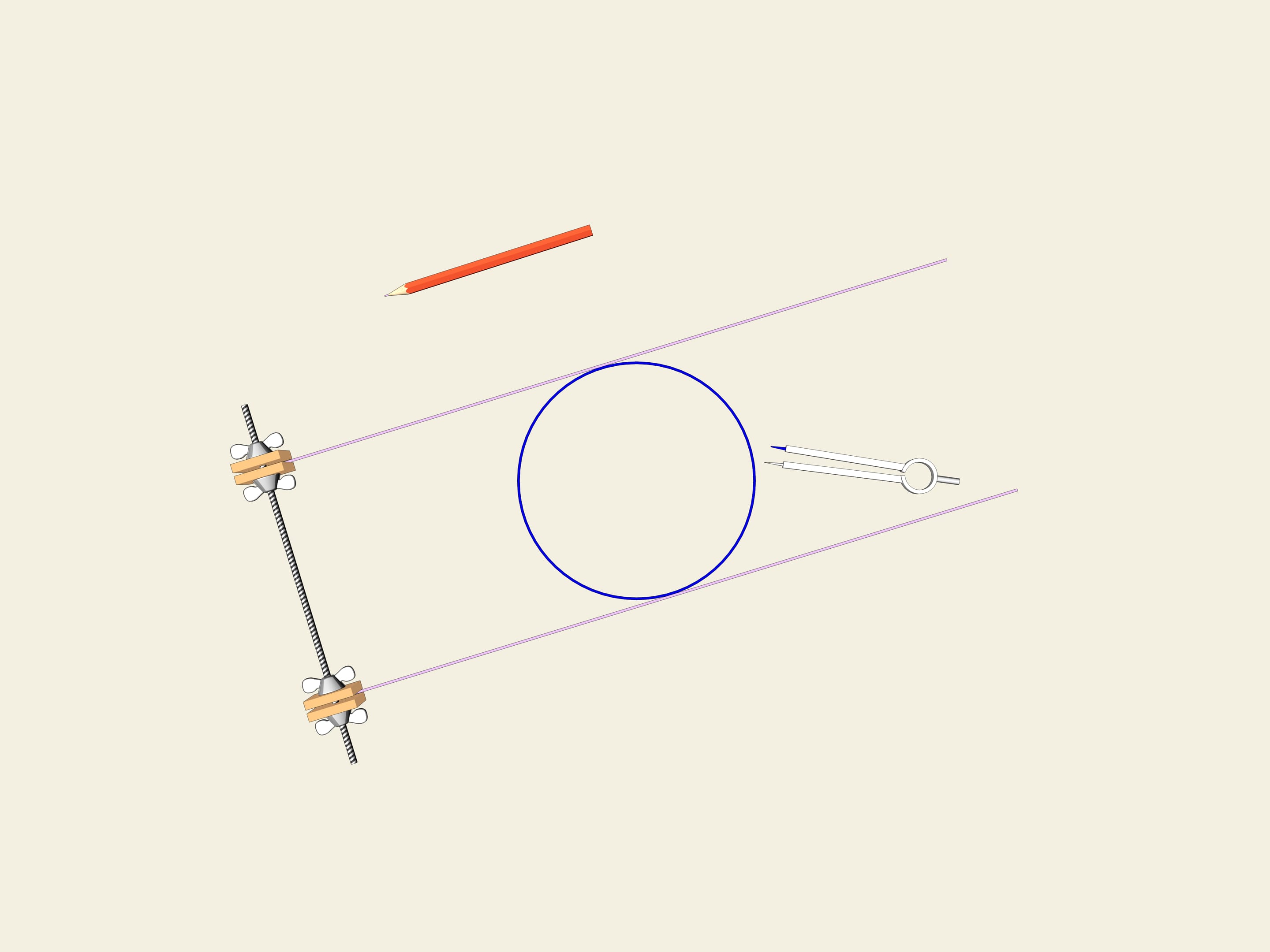
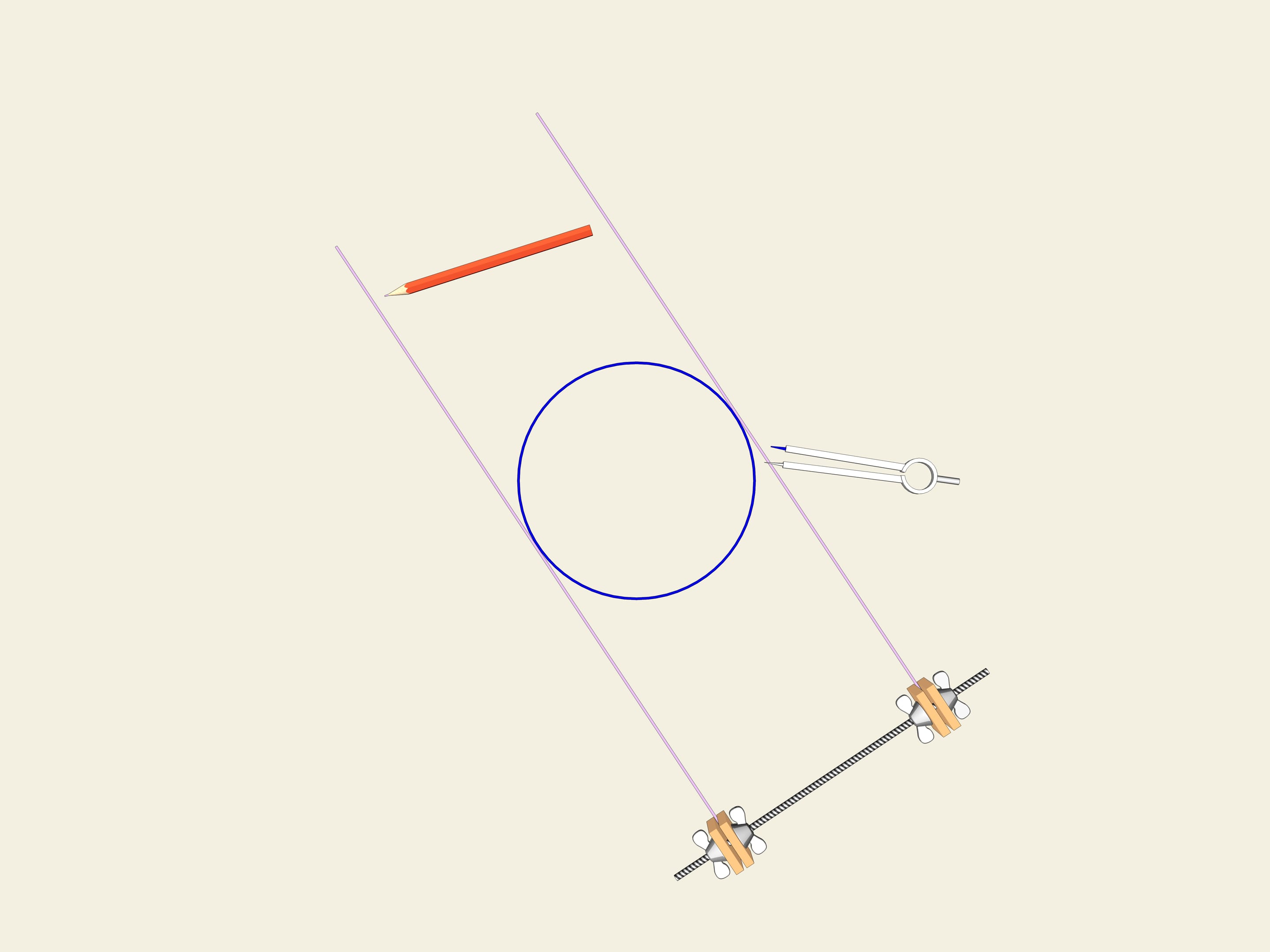
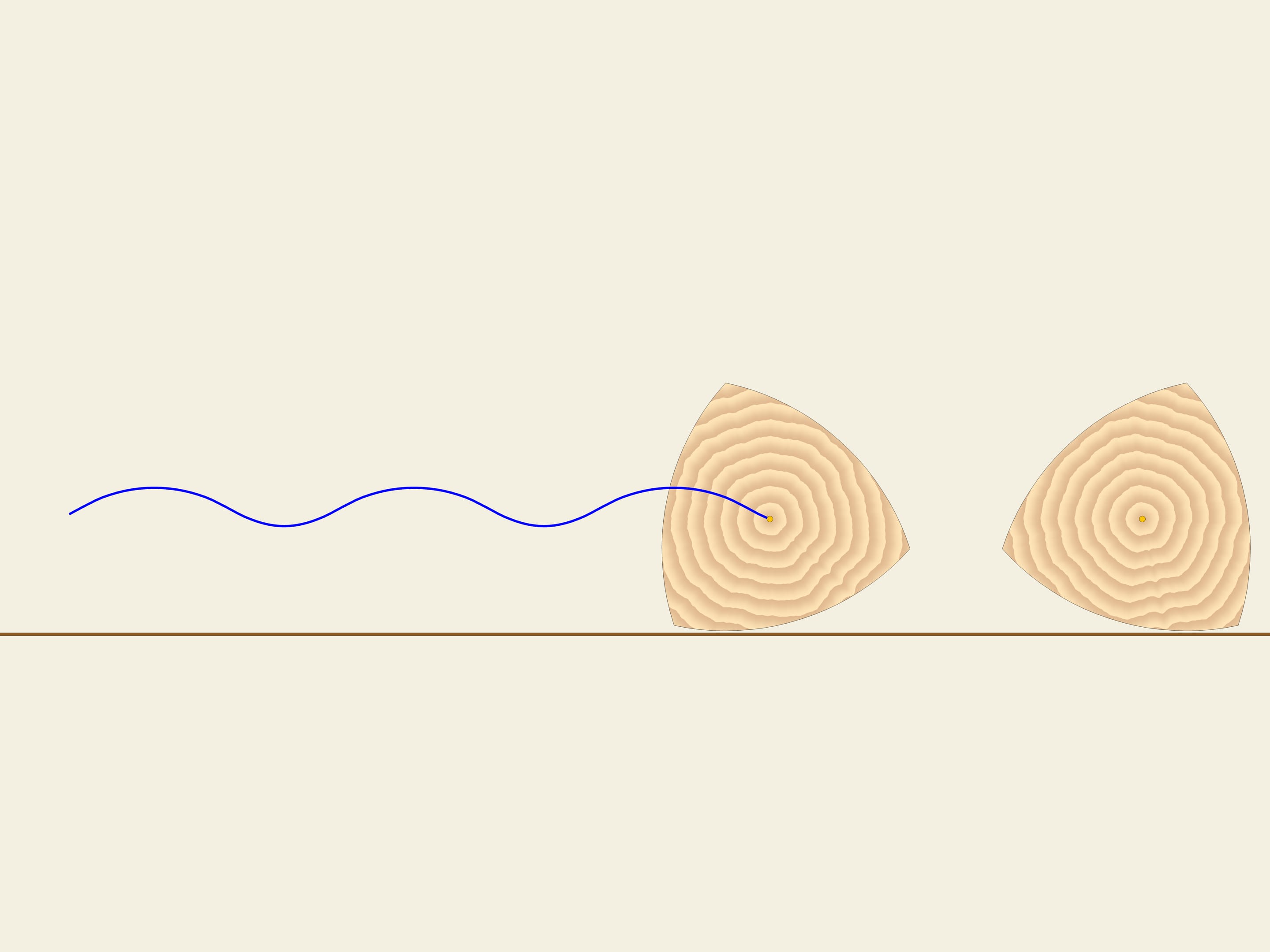
Prendiamo una ruota, ossia, un cerchio. Una delle proprietà del cerchio è la sua larghezza costante. Tracciamo due tangenti parallele al cerchio, e fissiamone la distanza. Cominciamo a farle girare. La curva (nel nostro caso il cerchio) è sempre a contatto con entrambe le linee.

Questa è la definizione stessa di una curva chiusa avente larghezza costante.

Esistono curve diverse dal cerchio che hanno larghezza costante?

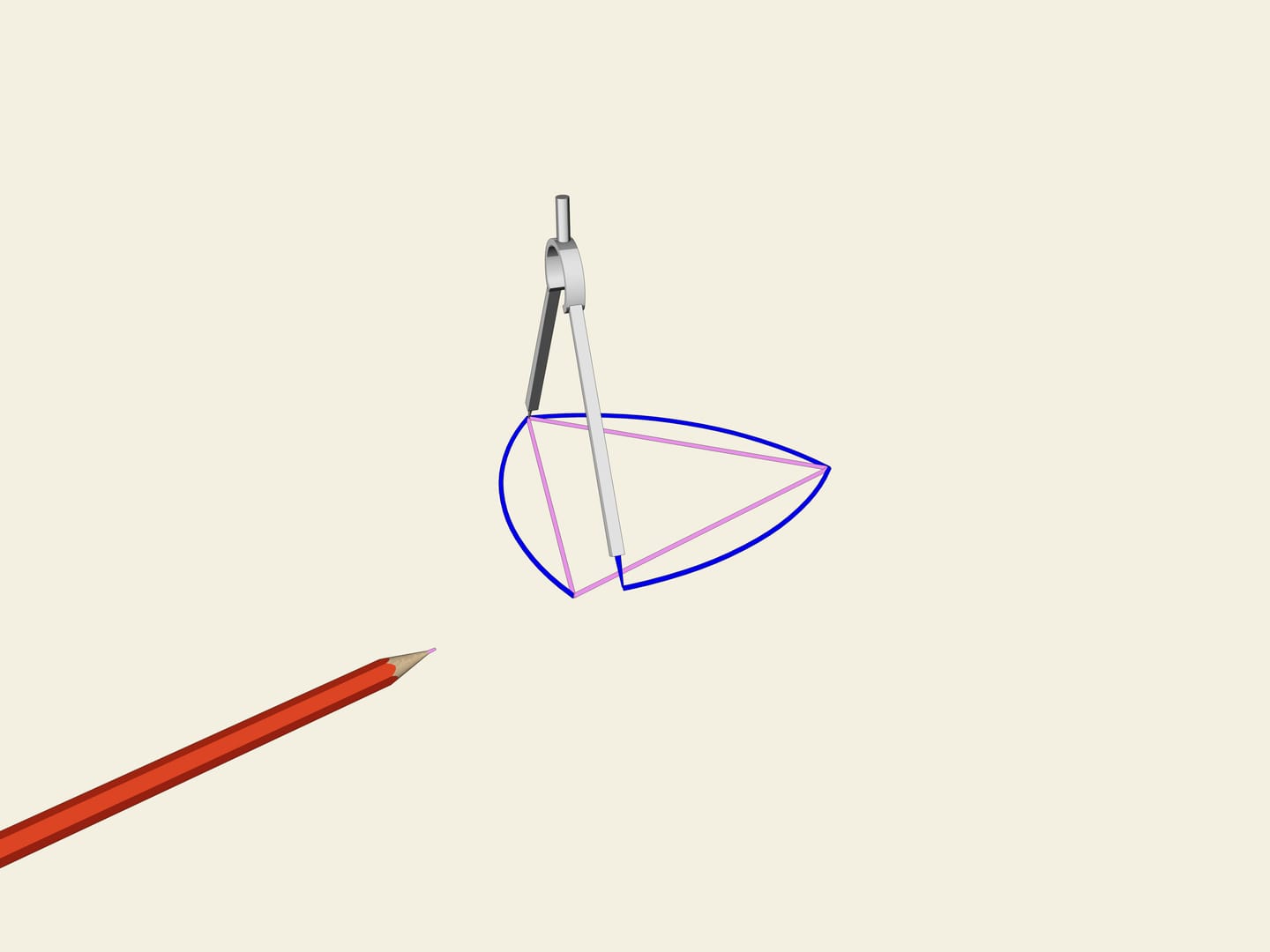
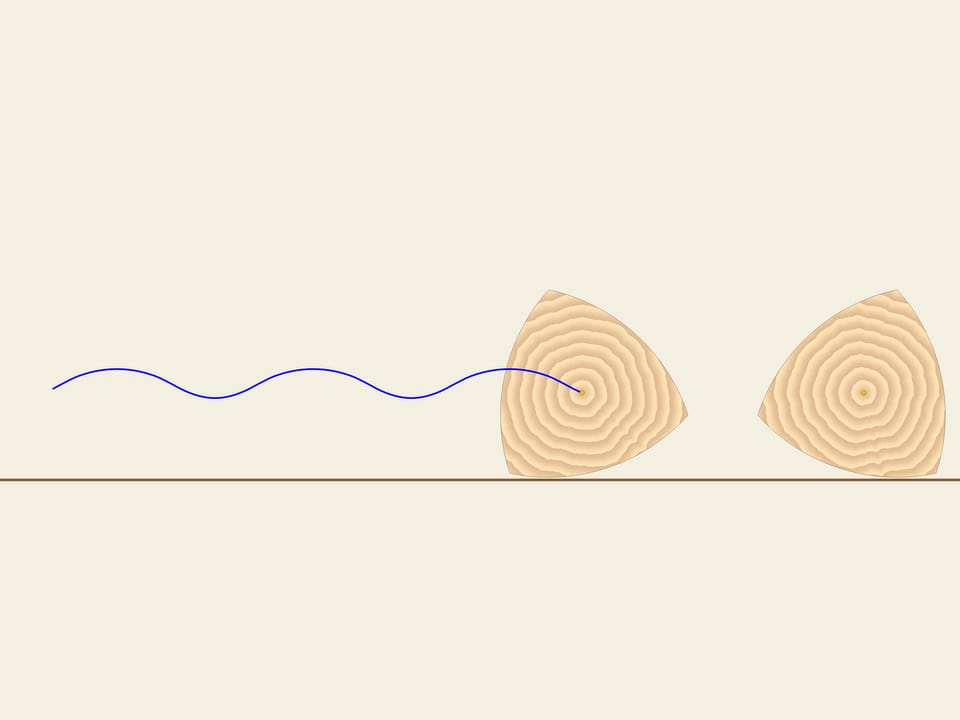
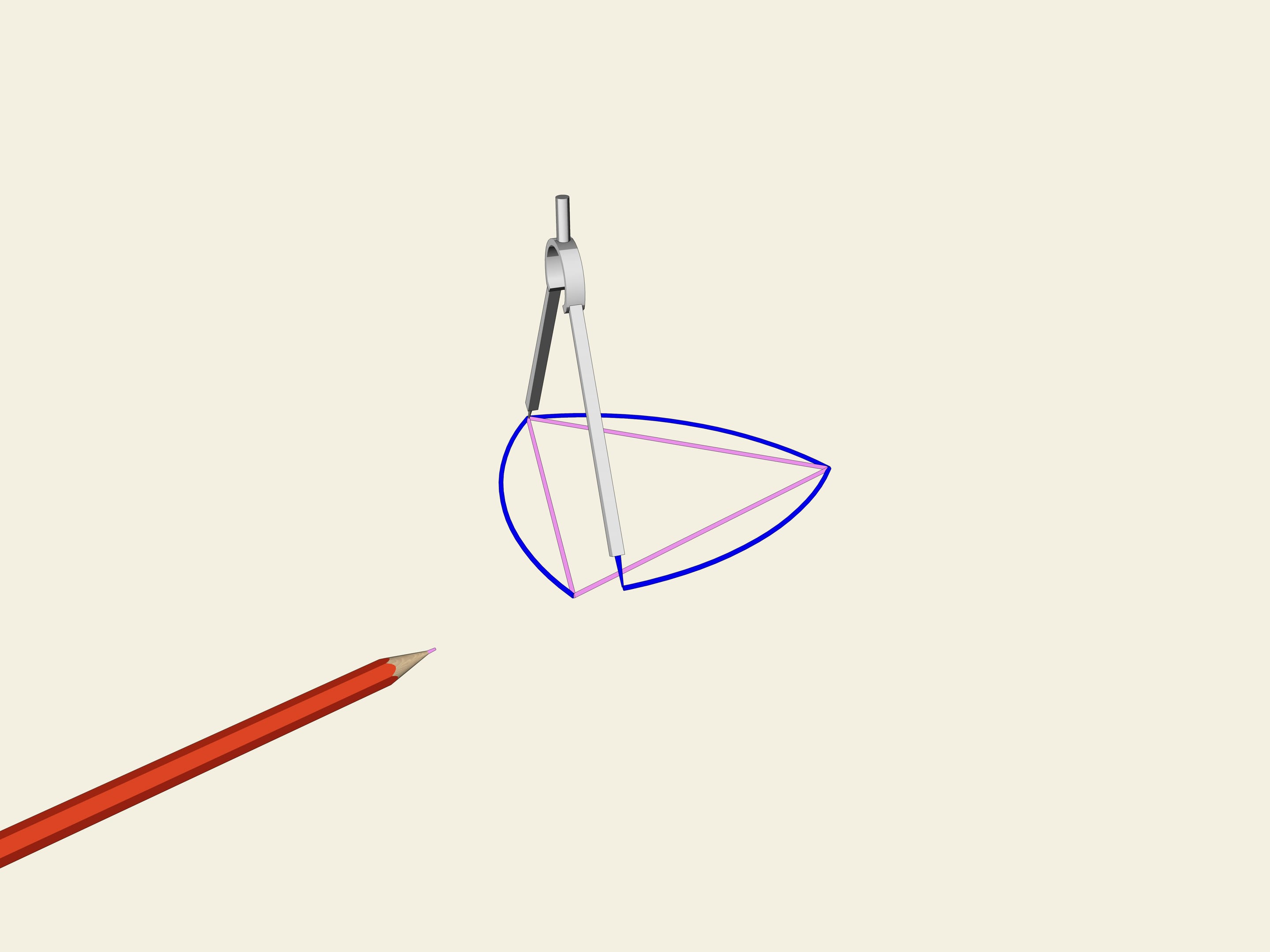
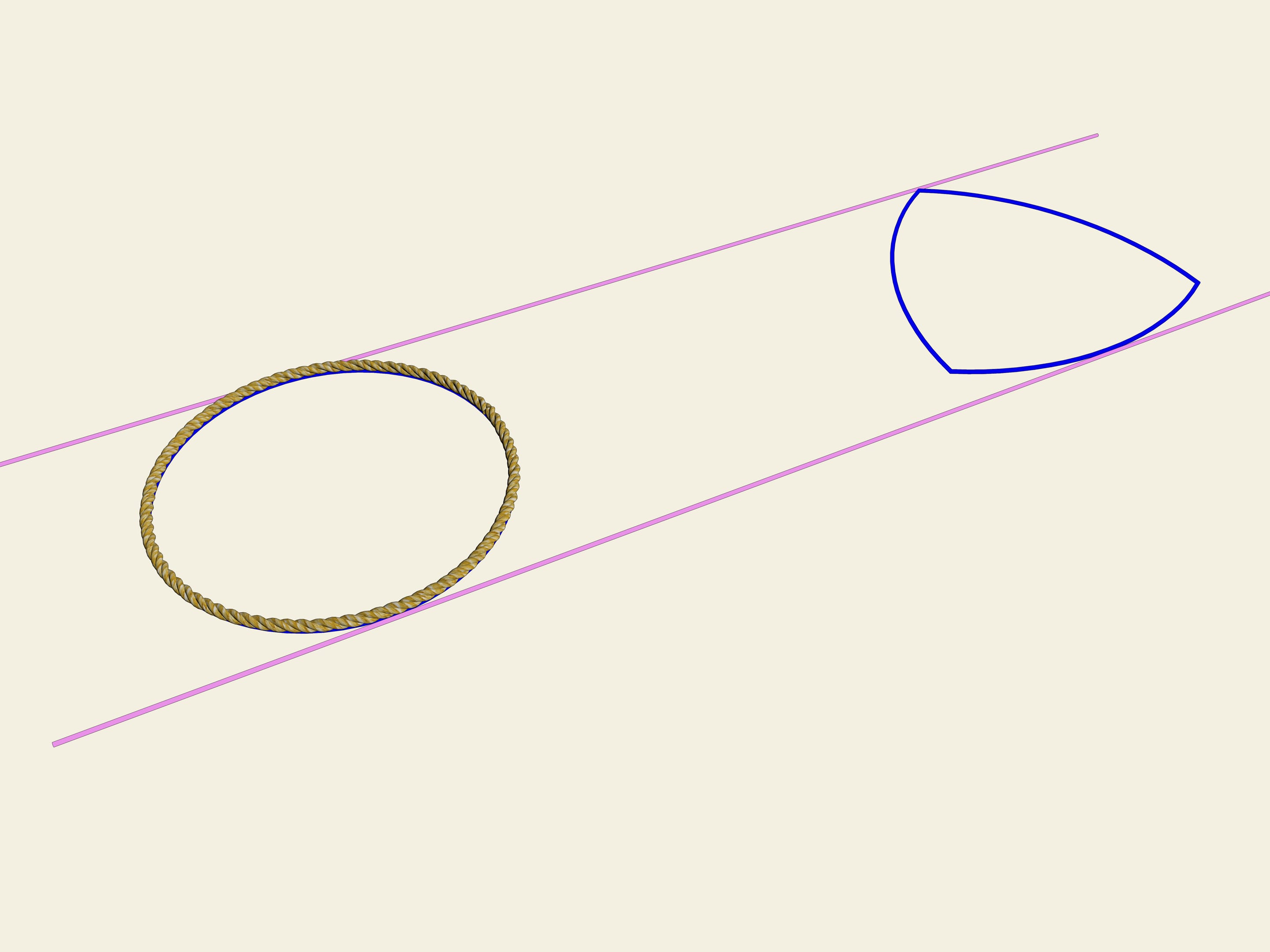
Si consideri un triangolo equilatero (con i lati uguali). Su ogni lato si costruisce un arco di cerchio con raggio uguale alla lunghezza del lato. Questa curva porta il nome di “triangolo di Reuleaux”.

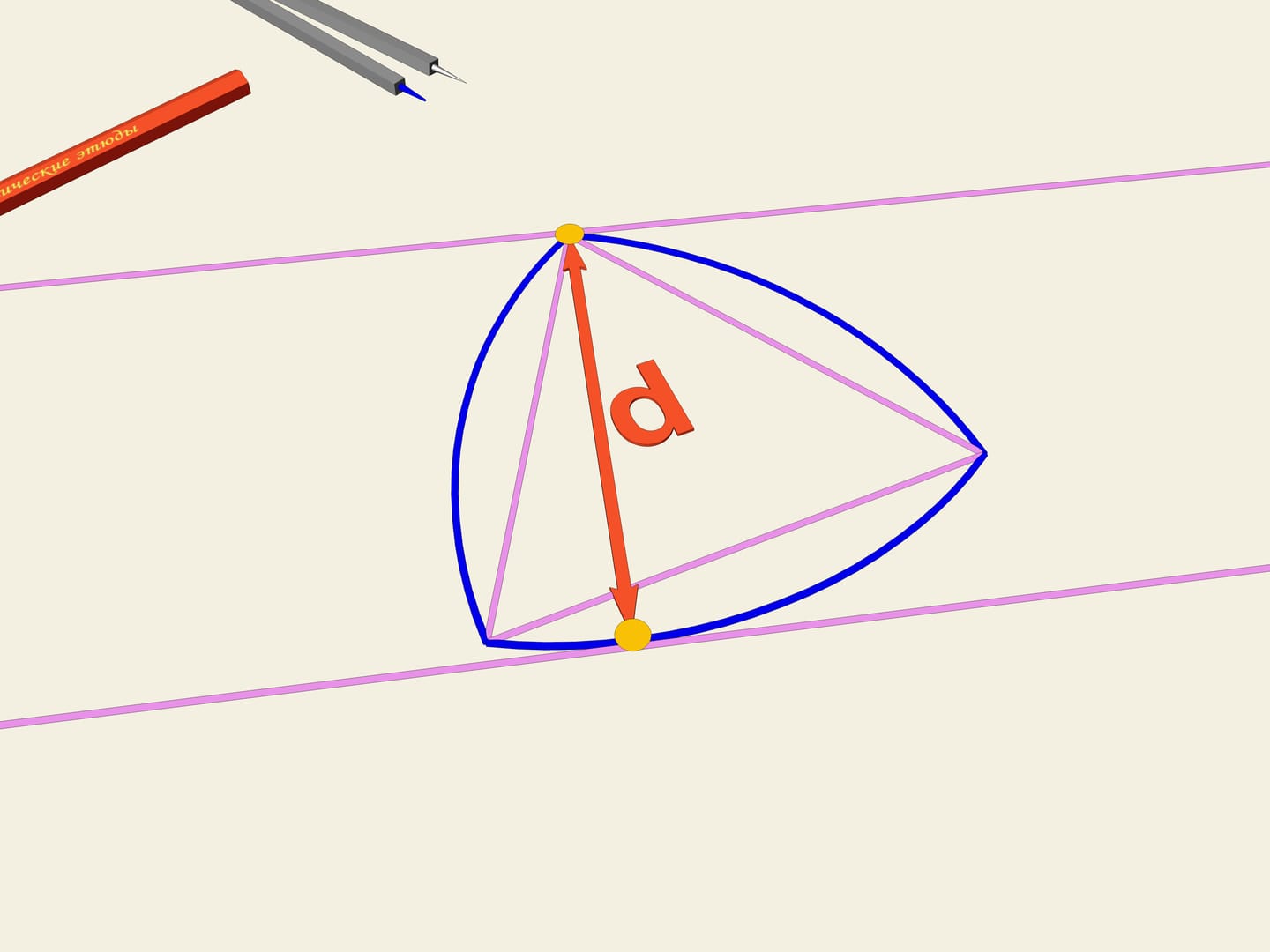
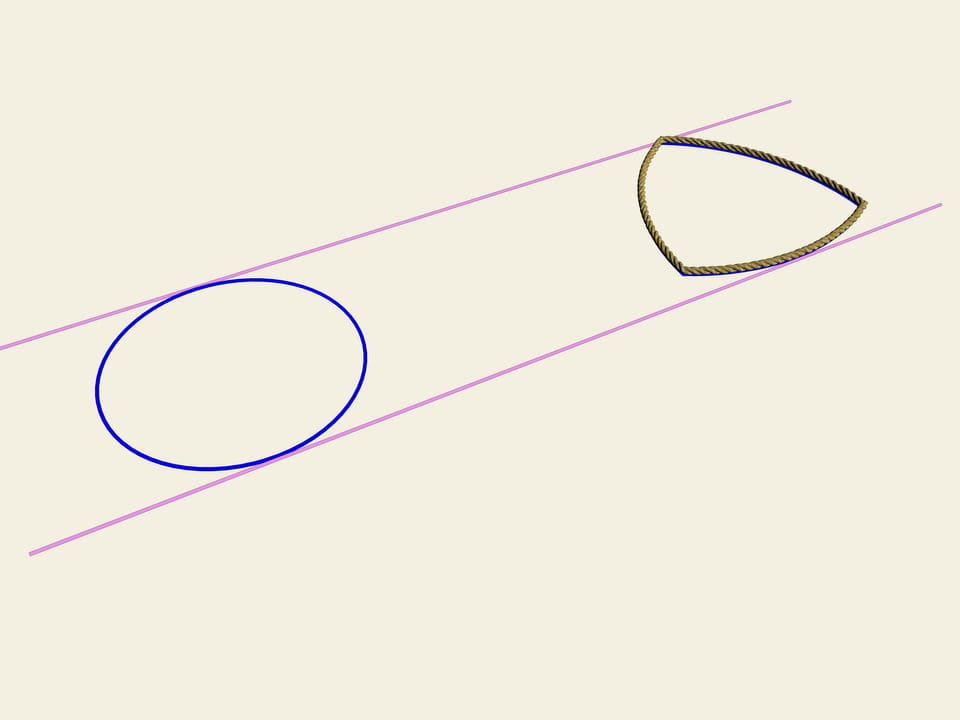
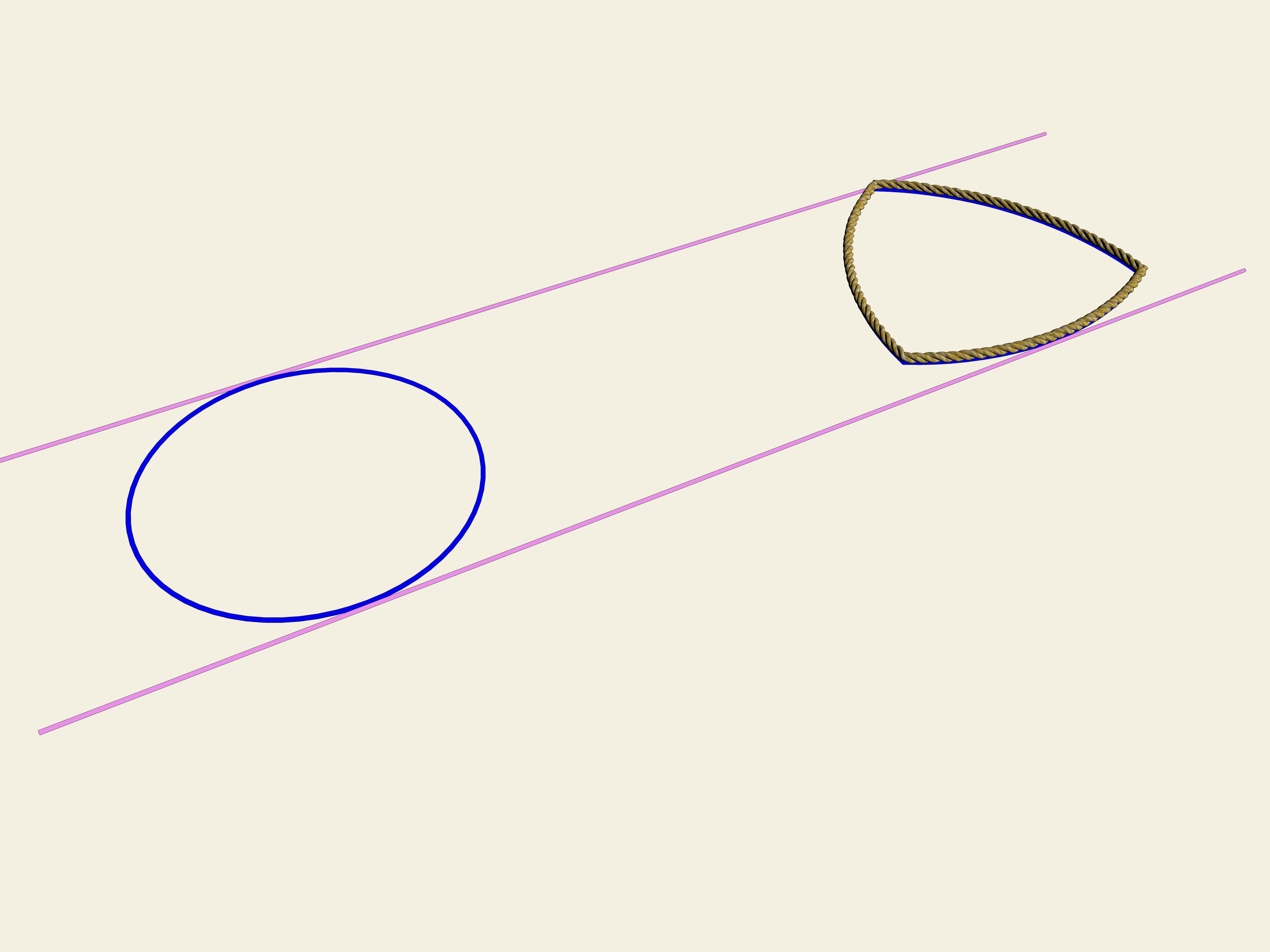
Accade che anche questa curva ha larghezza costante. Come nel caso del cerchio, prendiamo due rette parallele, fissiamo la distanza tra di esse e incominciamo a farle girare. Il triangolo di Reuleaux è costantemente a contatto di entrambe le parallele. Infatti, un punto di contatto è sempre situato in uno dei vertici del triangolo di Reuleaux, mentre l’altro punto, sull’altra parallela, è un punto di tangenza con l’arco di cerchio opposto. Ciò significa che la larghezza è sempre uguale al raggio della circonferenza, cioè alla lunghezza del lato del triangolo equilatero.

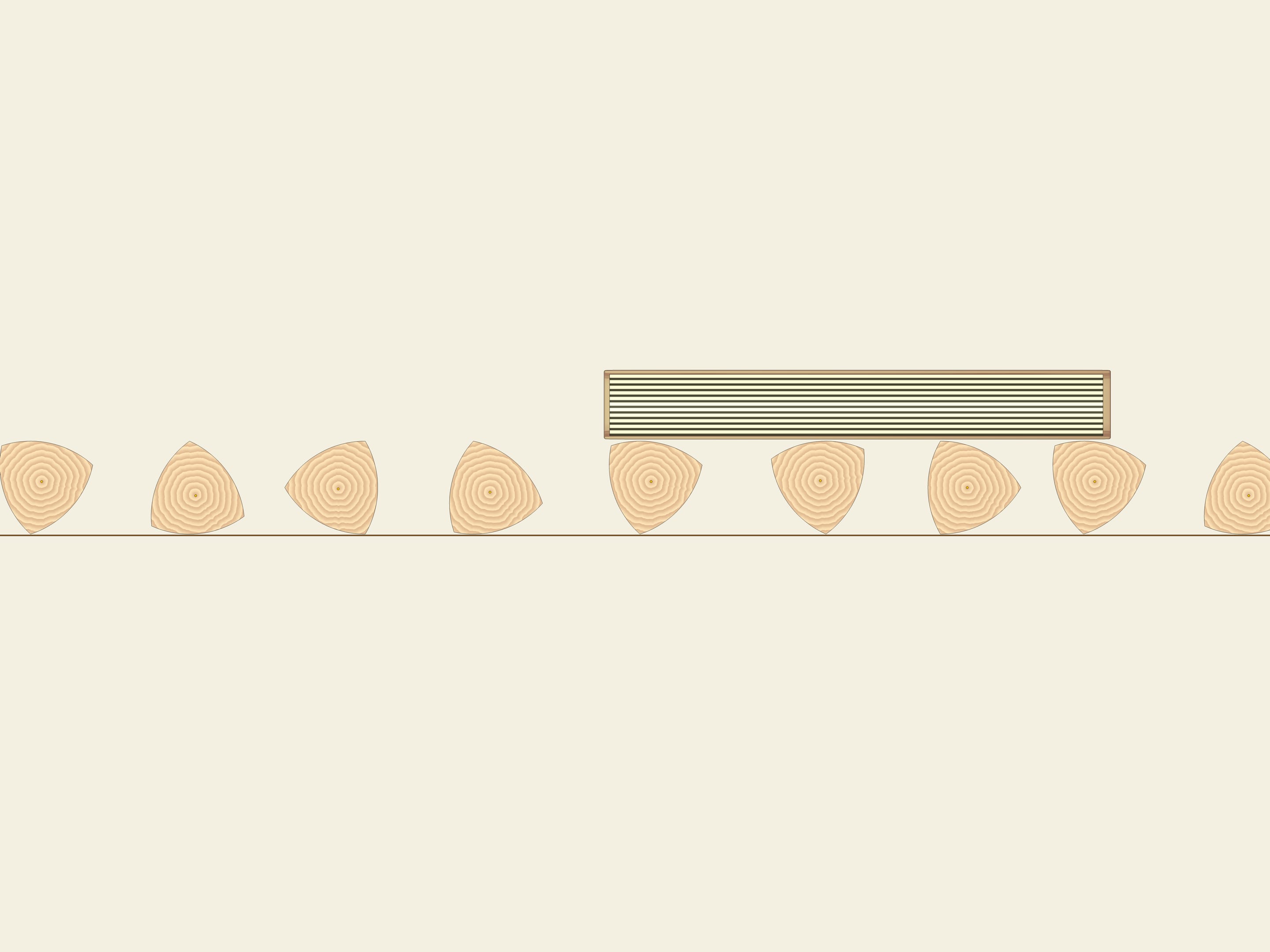
Nella pratica, la larghezza costante di questa curva implica che se costruiamo dei rulli che hanno per sezione tale curva, il libro rotolerà su di essi, restando perfettamente orizzontale.

Tuttavia, non si può costruire un carrello avente le ruote con questo profilo, perché il centro di tali ruote descrive una linea complicata mentre queste rotolano su di un terreno rettilineo.

Esistono altre curve di larghezza costante? Sì, ce ne sono, in effetti, un’infinità.

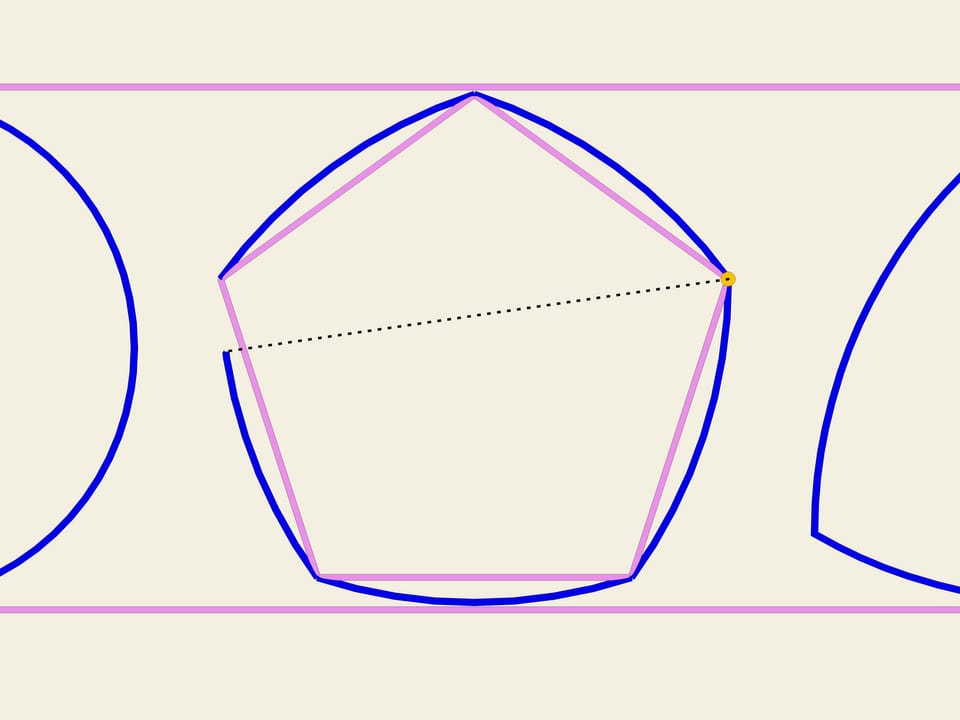
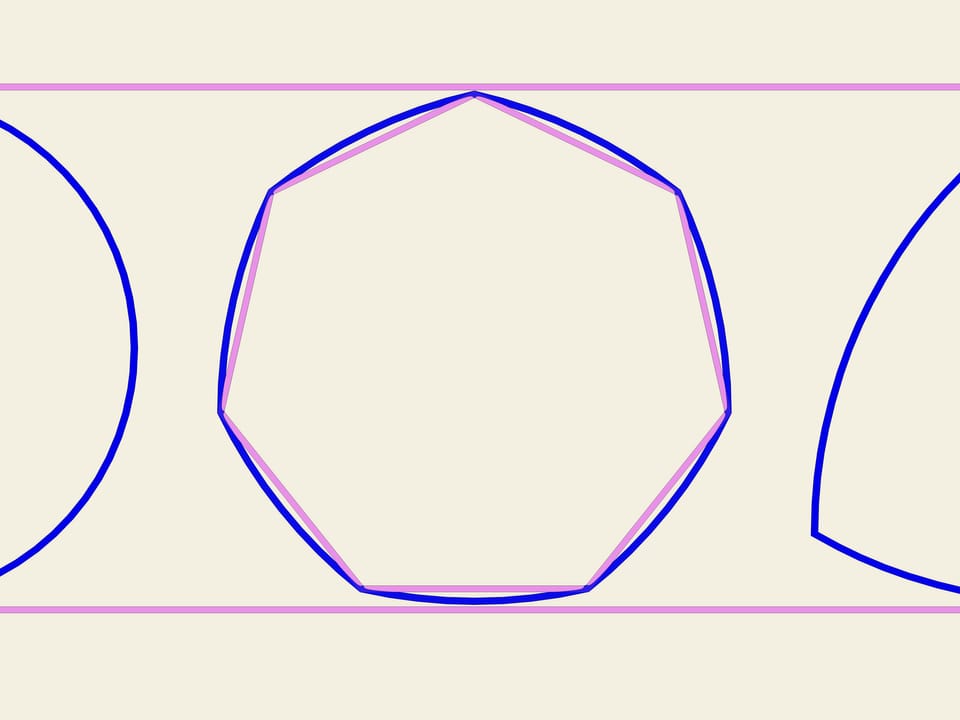
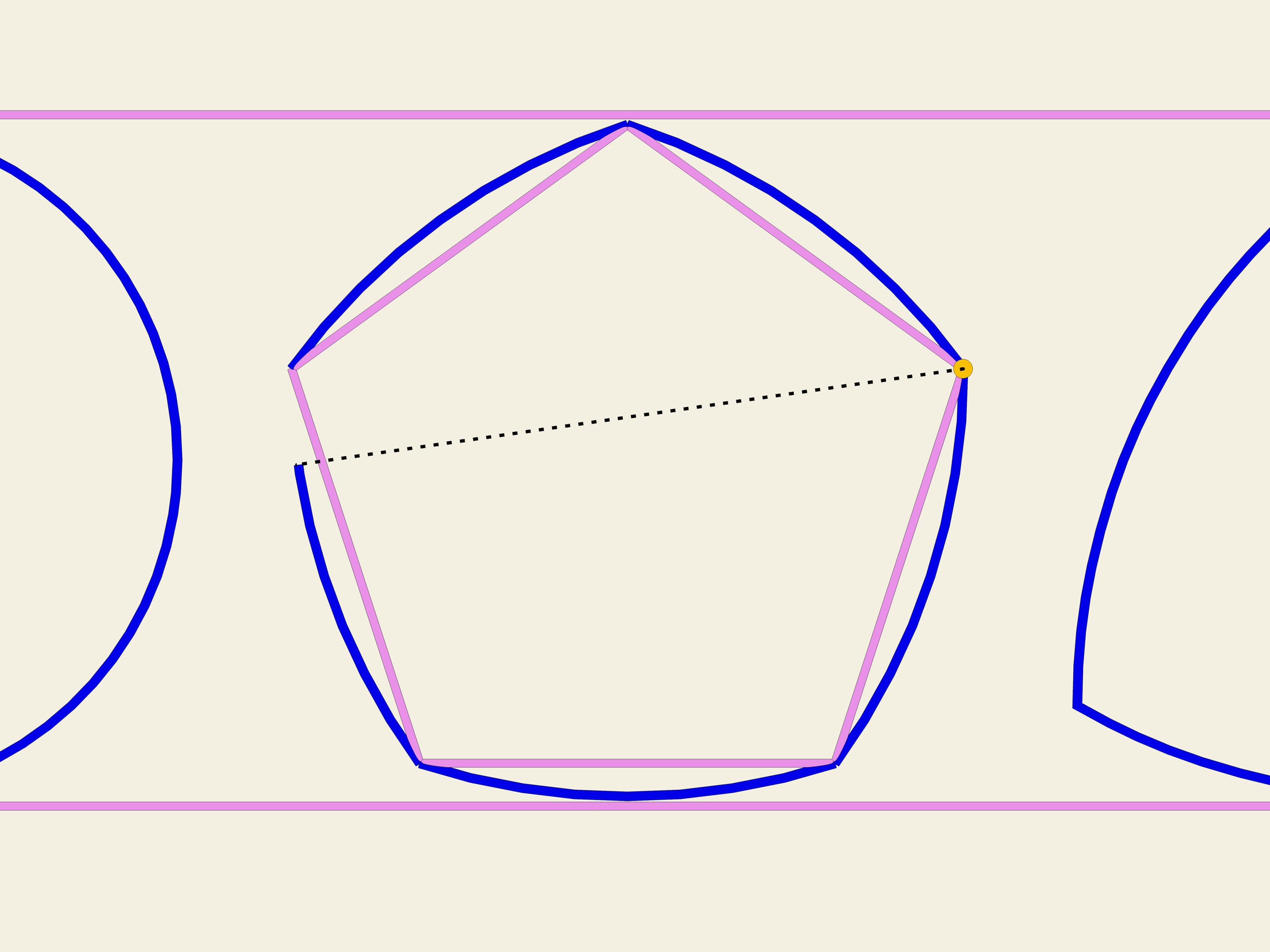
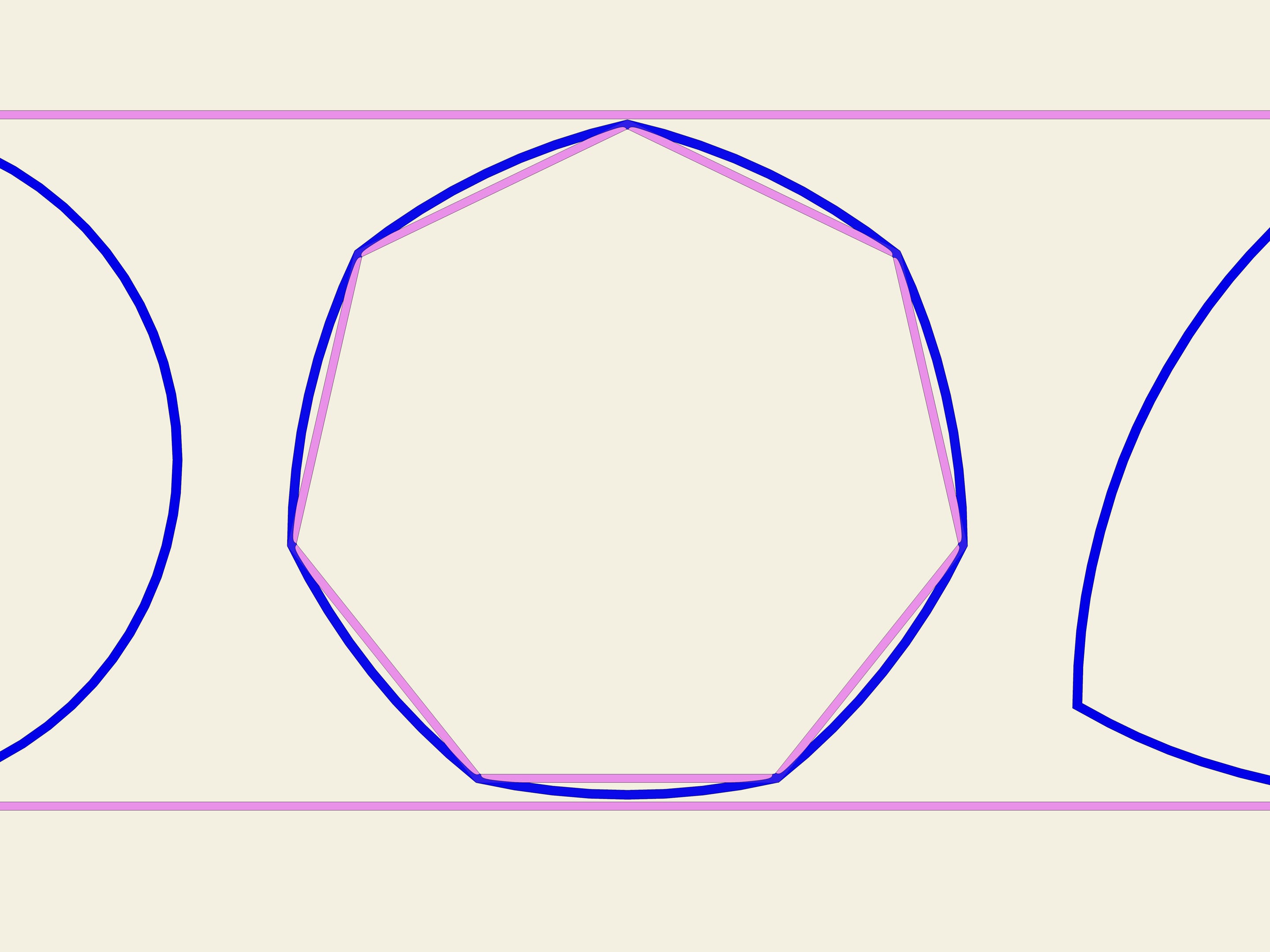
Partendo da un qualsiasi poligono regolare con un numero dispari di lati si può costruire una curva di larghezza costante usando la stessa procedura usata per costruire il triangolo di Reuleaux. Usando ogni vertice come centro, tracciamo un arco di cerchio tra i due vertici dello spigolo opposto.

In Inghilterra, la moneta da 20 pence ha la forma di una curva di larghezza costante, costruita su un ettagono.

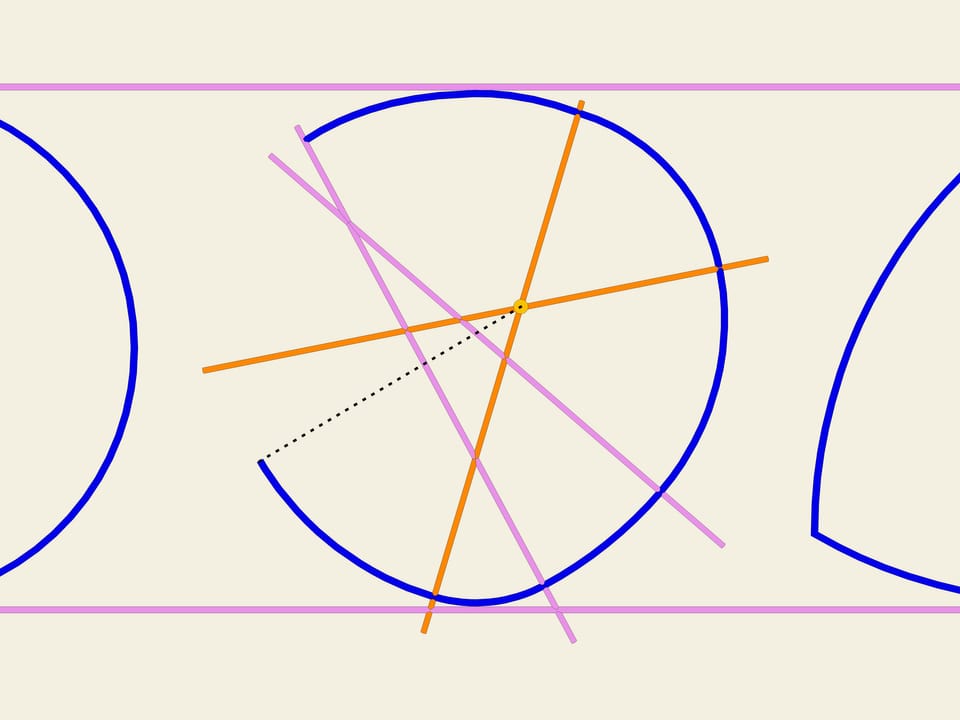
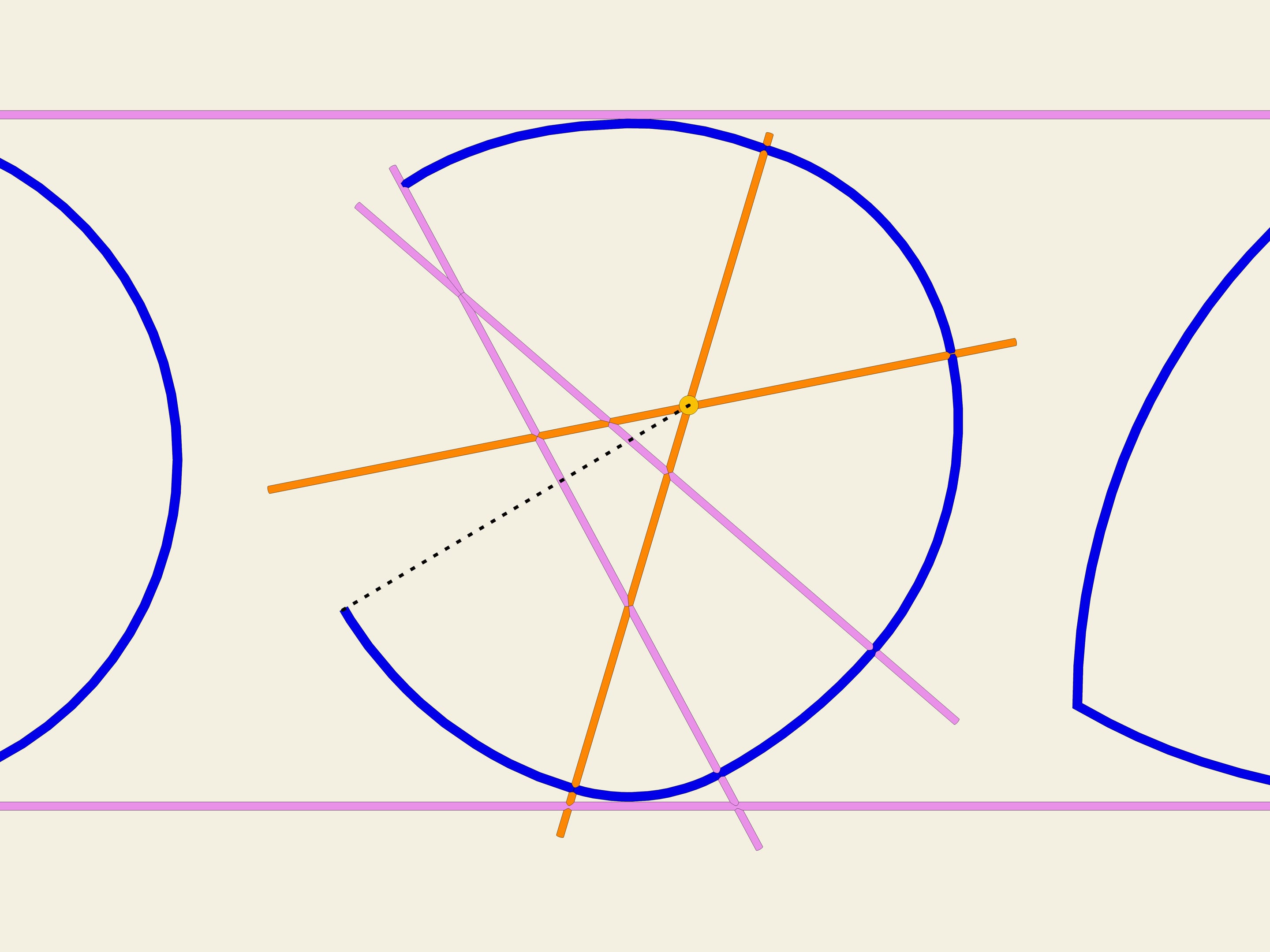
Ma le curve considerate non esauriscono la lista di tutte le curve a larghezza costante. Tra loro, infatti, esistono anche delle curve non simmetriche. Consideriamo n rette su un piano che si intersecano in modo casuale (che non siano tra loro parallele). Esse individuano 2n settori illimitati del piano. Ognuno di questi settori ha due lati che vanno all’infinito. Il punto di incontro di questi due lati lo prendiamo come centro, e tracciamo un arco di cerchio, di raggio abbastanza grande, congiungente due punti di questi lati. Quindi passiamo al settore adiacente e tracciamo un arco in modo simile, questa volta il suo raggio sarà determinato dal fatto che deve prolungare con continuità l’arco precedente.

Continuiamo fino ad esaurire tutti i settori. La curva così ottenuta, composta di archi di cerchio, è una curva chiusa di larghezza costante. Dimostratelo!

Tutte le curve di una data larghezza hanno la stessa lunghezza. Il cerchio e il triangolo di Reuleaux aventi stessa larghezza hanno in comune anche la proprietà di essere curve estremali , tra tutte le curve di quella stessa larghezza: il cerchio racchiude la superficie di area massima, e il triangolo di Reuleaux quella di area minima.

Il triangolo di Reuleaux non è interes­sante solo per i matematici; questa figure ha delle applicazioni sorprendenti in meccanica.

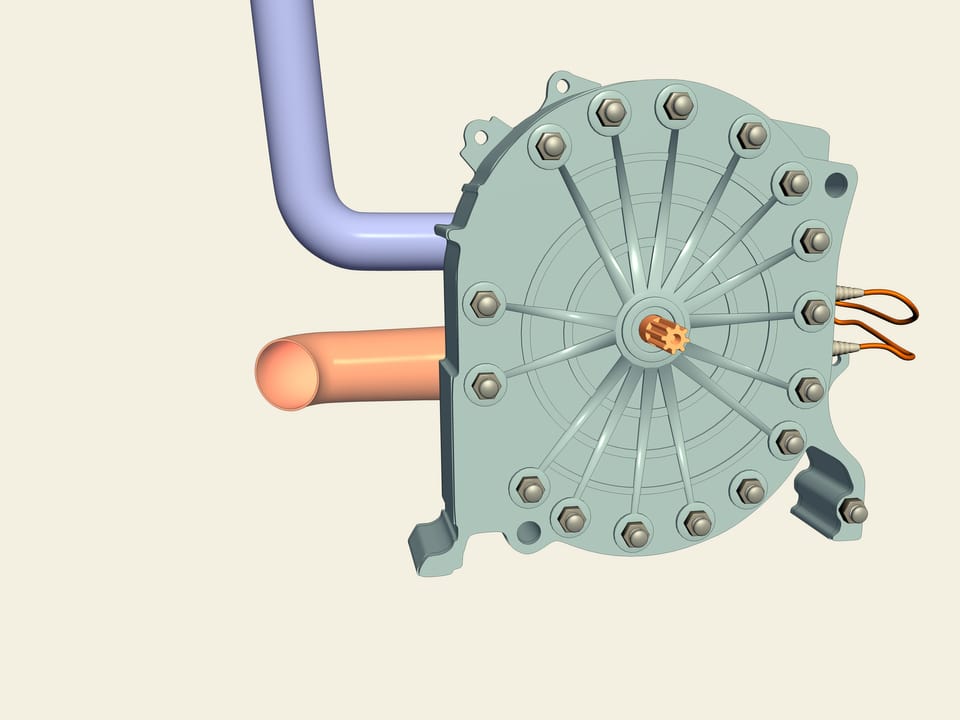
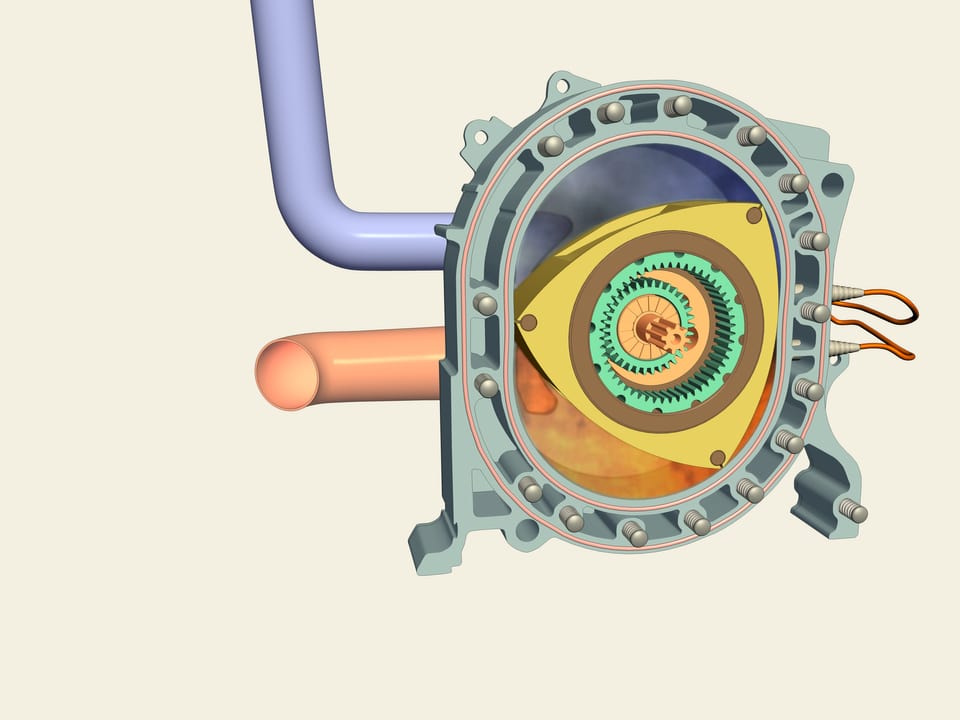
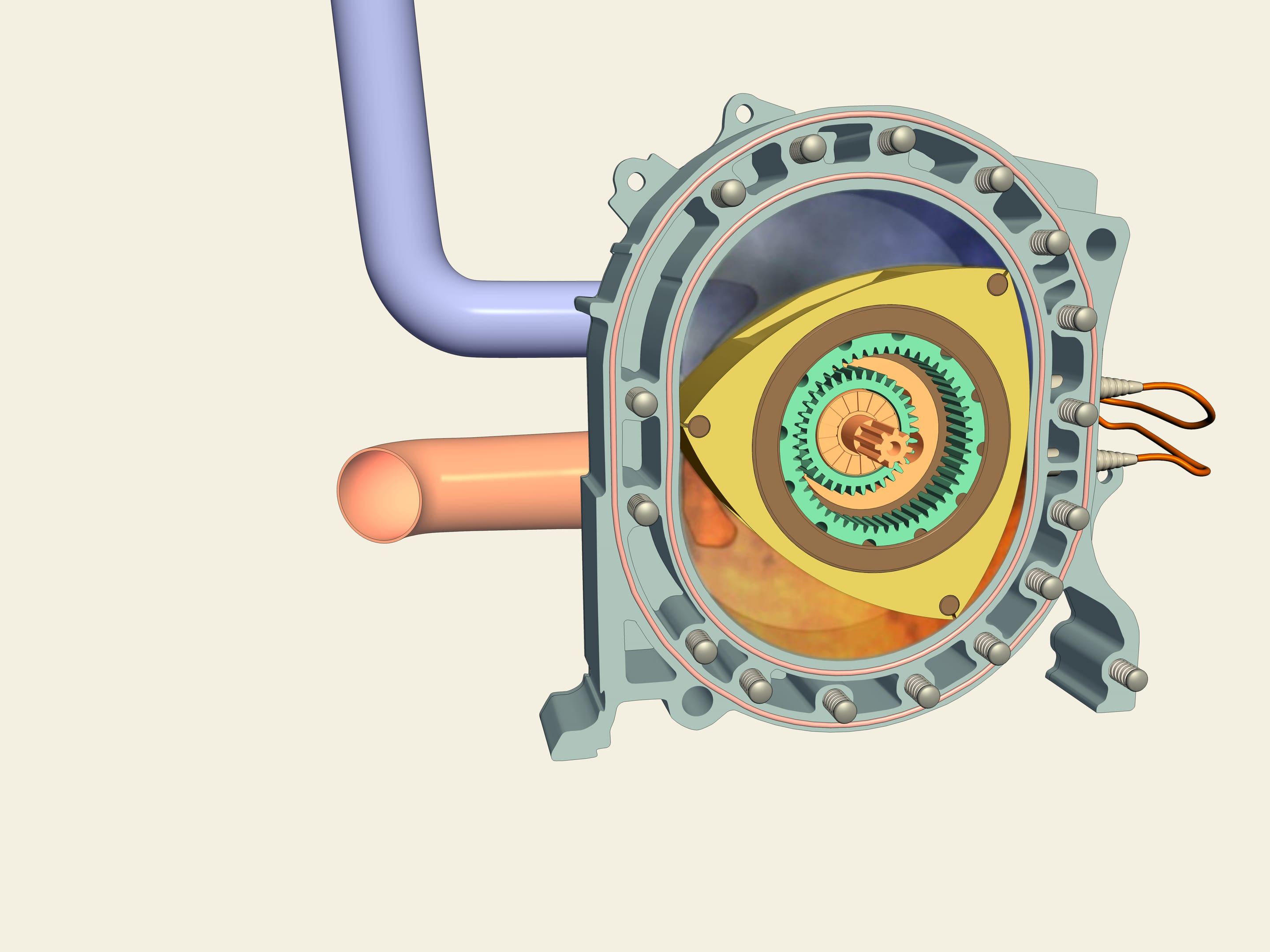
Osservate: questa è una “Mazda RX-7” A differenza della maggioranza delle auto, in essa (così come nel modello RX-8) c’è un motore rotativo Wankel. Come è fatto? Come rotore viene utilizzato proprio un triangolo di Reuleaux! Tra di esso e le pareti si formano tre camere, ognuna delle quali è a turno una camera di combustione. Viene dunque introdotta la miscela blu di benzina che poi, a causa del movimento del rotore, viene compressa, e poi, scoppiando, fa girare il rotore. Il motore rotativo è privo di alcune delle carenze della contro­parte a pistone: la rotazione è direttamente trasmessa all’asse e non è quindi neces­sario usare l’albero di trasmis­sione.

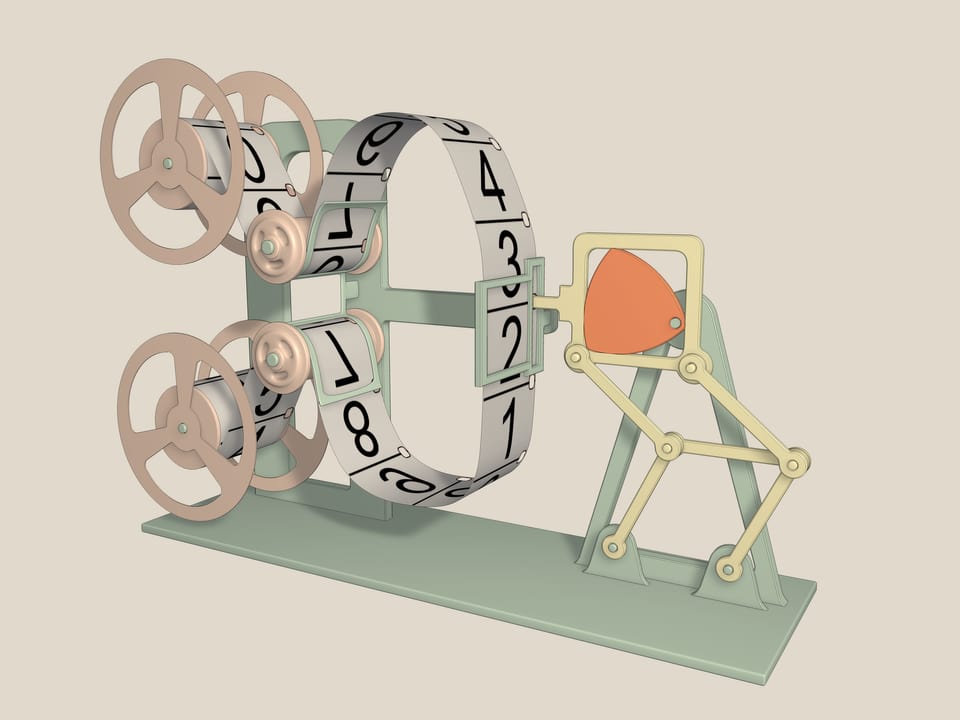
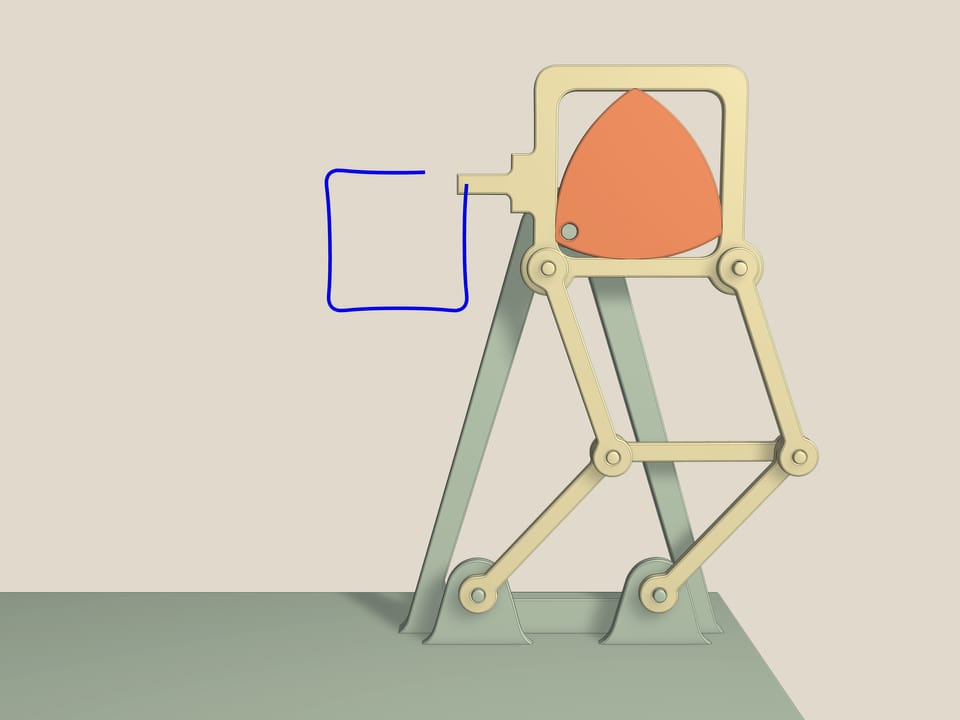
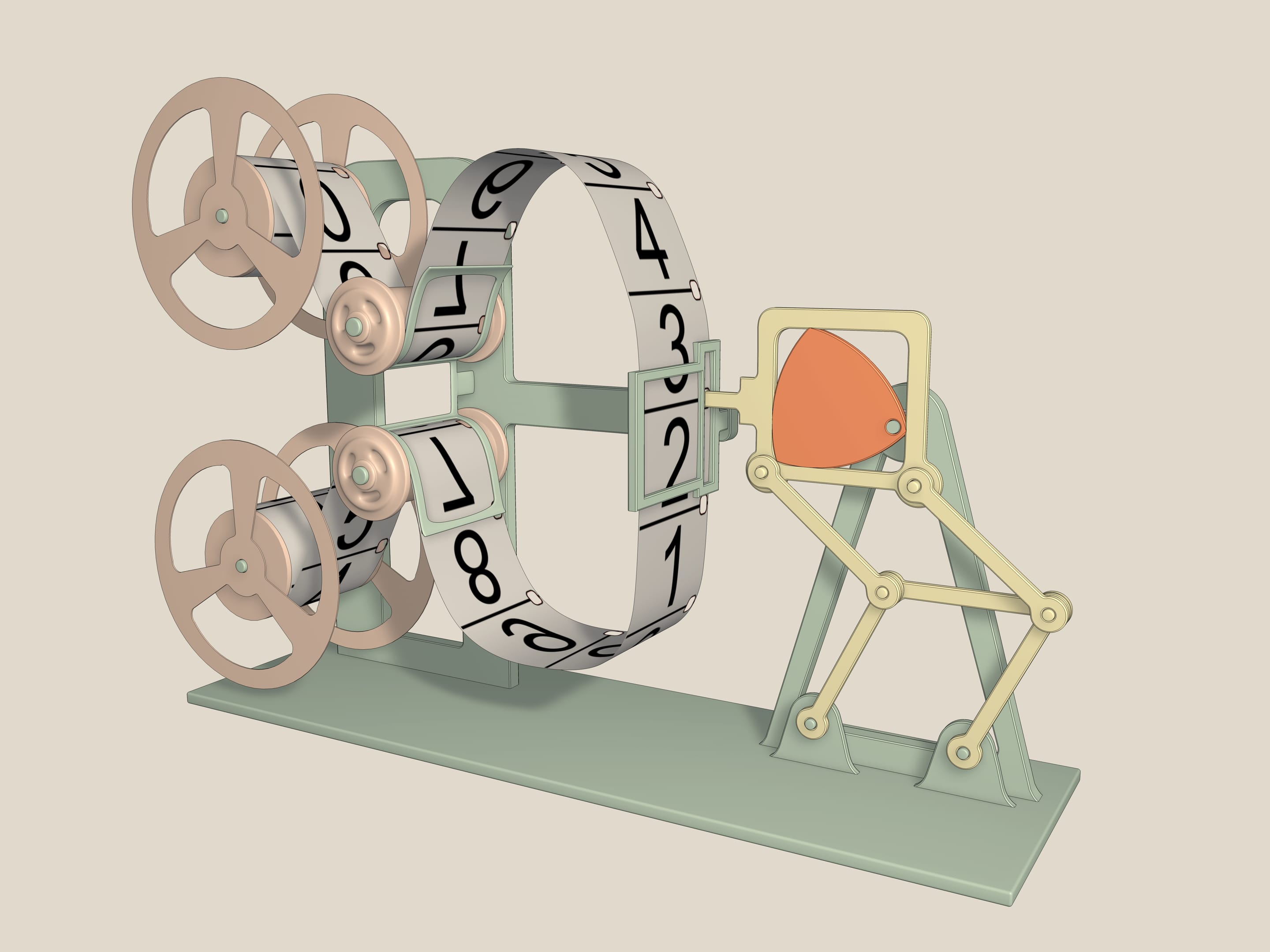
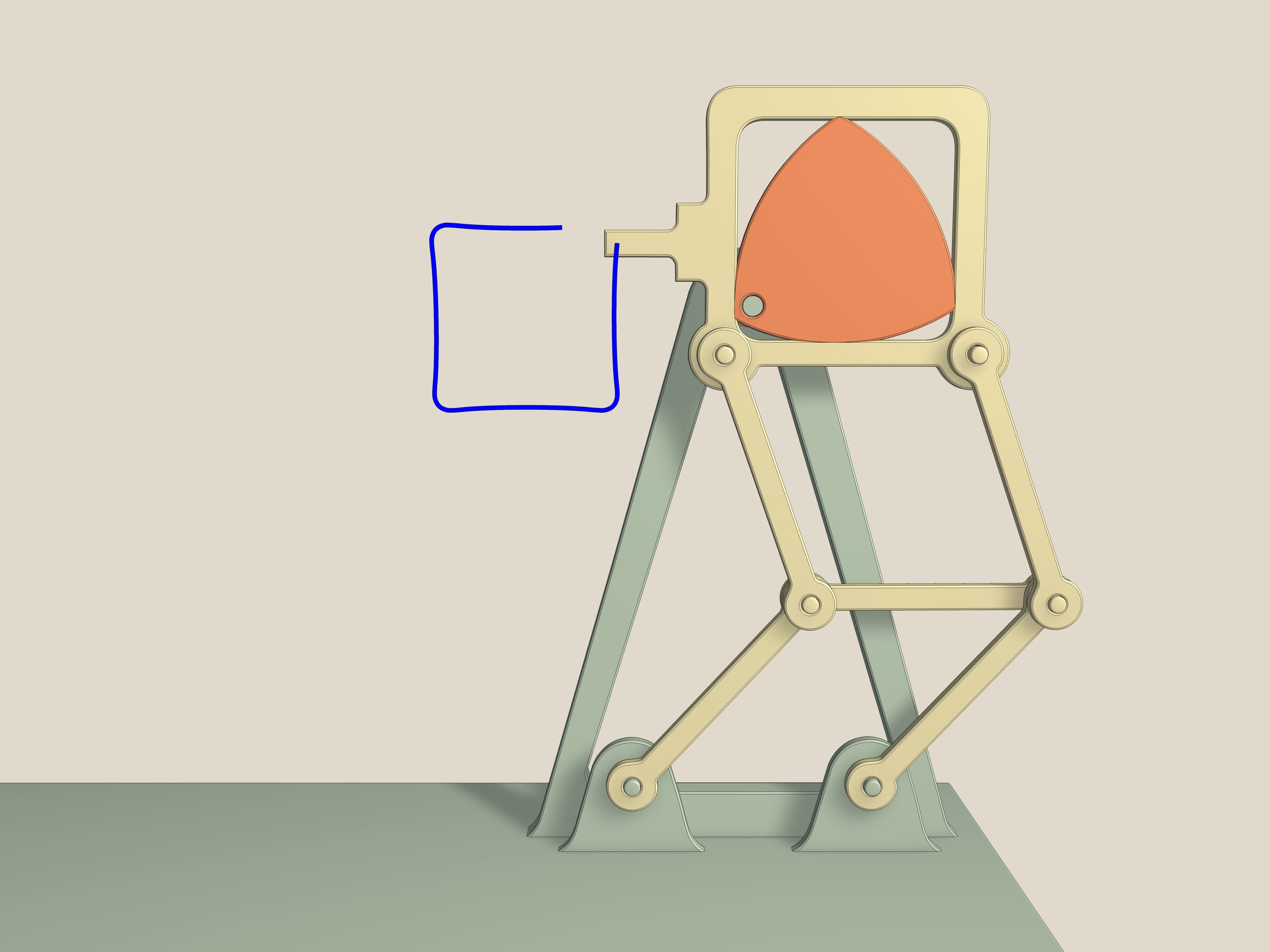
Quest’altro invece è un meccanismo di proiezione di pellicole cinematografiche. Il motore di una cinepresa, infatti, genera una rotazione continua intorno ad un’asse, ma al fine di avere sullo schermo delle immagini nette, bisogna che ogni fotogramma rimanga immobile per qualche istante e che il passaggio tra un fotogramma al succes­sivo avvenga in un tempo molto più breve. Tutto questo 18 volte al secondo. Questo problema viene di fatto risolto proprio da un meccanismo, che si basa sul triangolo di Reuleaux, inscritto in un quadrato, e su un doppio parallelogramma, che impedisce al quadrato di inclinarsi da un lato. Infatti, dal momento che le lunghezze dei lati opposti sono uguali, l’elemento centrale in tutti i movimenti rimane parallelo alla base mentre il lato del quadrato è sempre parallelo all’elemento di mezzo. Quanto più l'asse di rotazione è vicino al vertice del triangolo di Reuleaux, tanto più il dentino del meccanismo descrive una figura pros­sima a un quadrato.

Avete dunque visto che applicazioni interesanti possono avere dei puri oggetti matematici.