Ombre ⁠

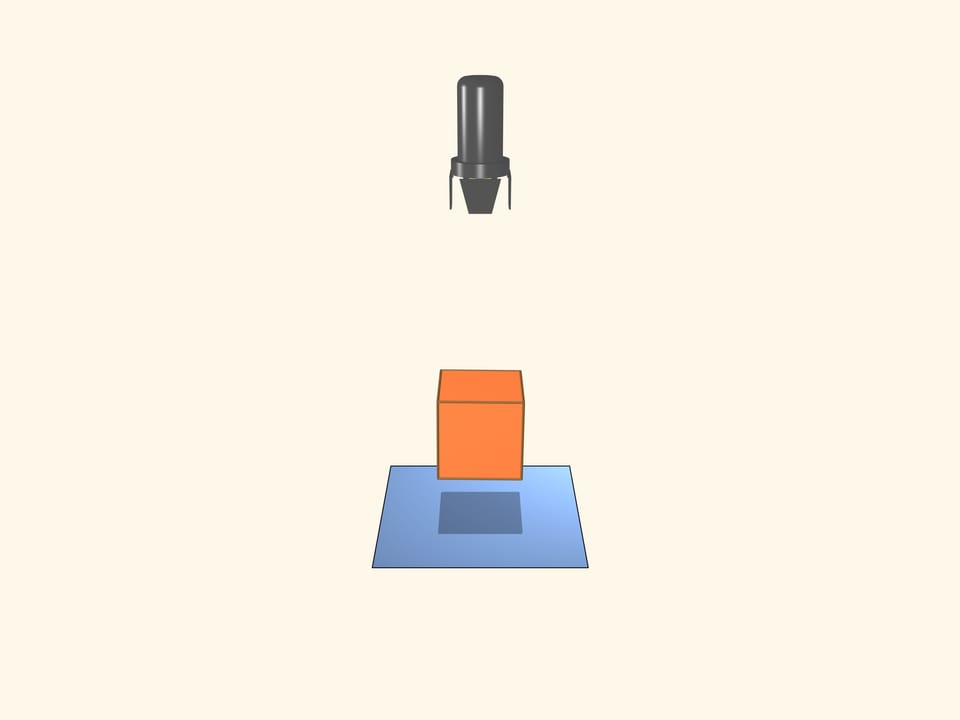
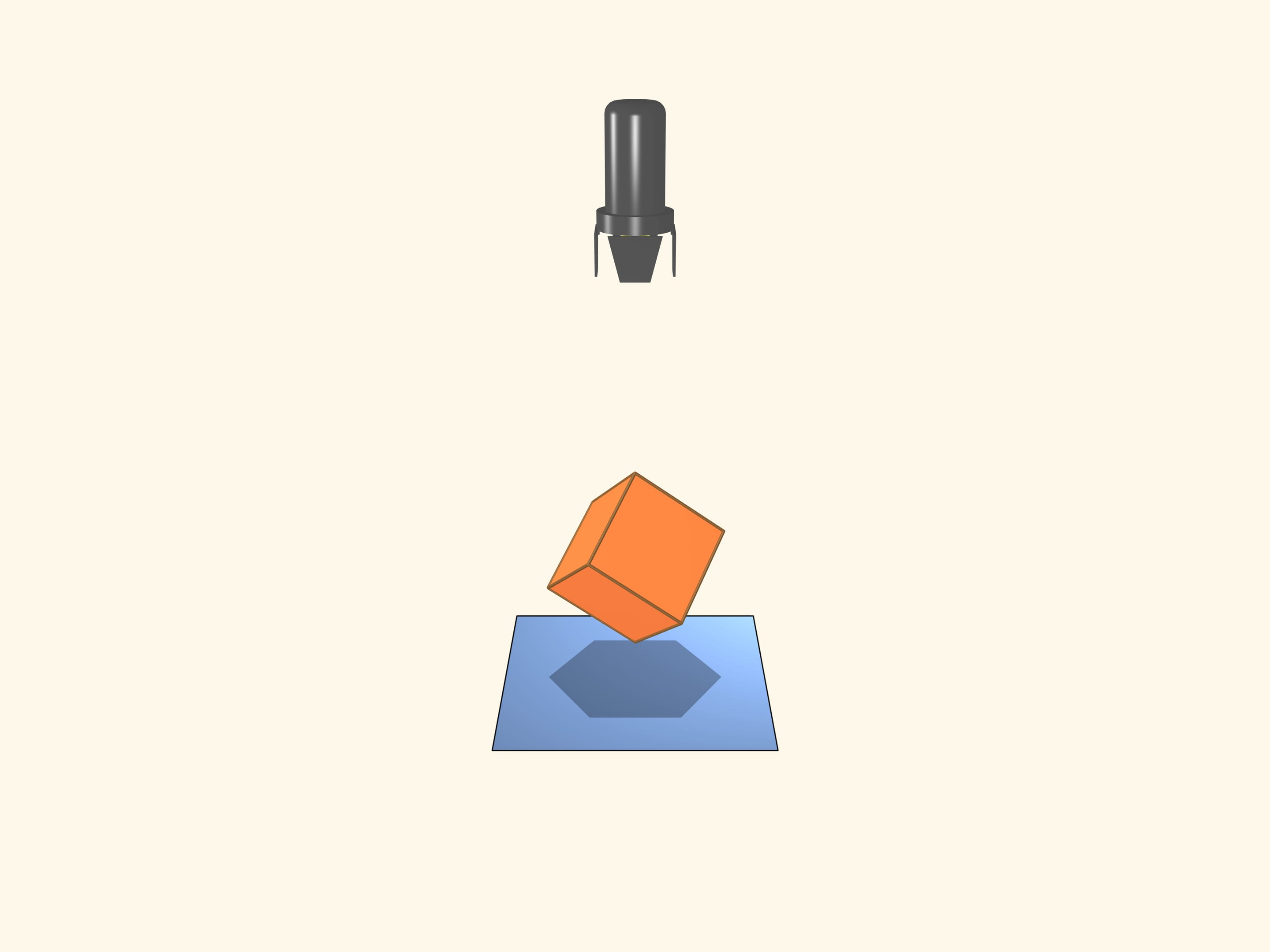
Prendiamo un proiettore, che emette raggi paralleli. Che l’ombra di un cubo abbia la forma di un quadrato risulta piuttosto evidente. Ma qual è il numero massimo di vertici di un poligono, che può essere l’ombra di un cubo? Se una diagonale del cubo è parallela ai raggi di luce, allora l’ombra sarà un esagono regolare!

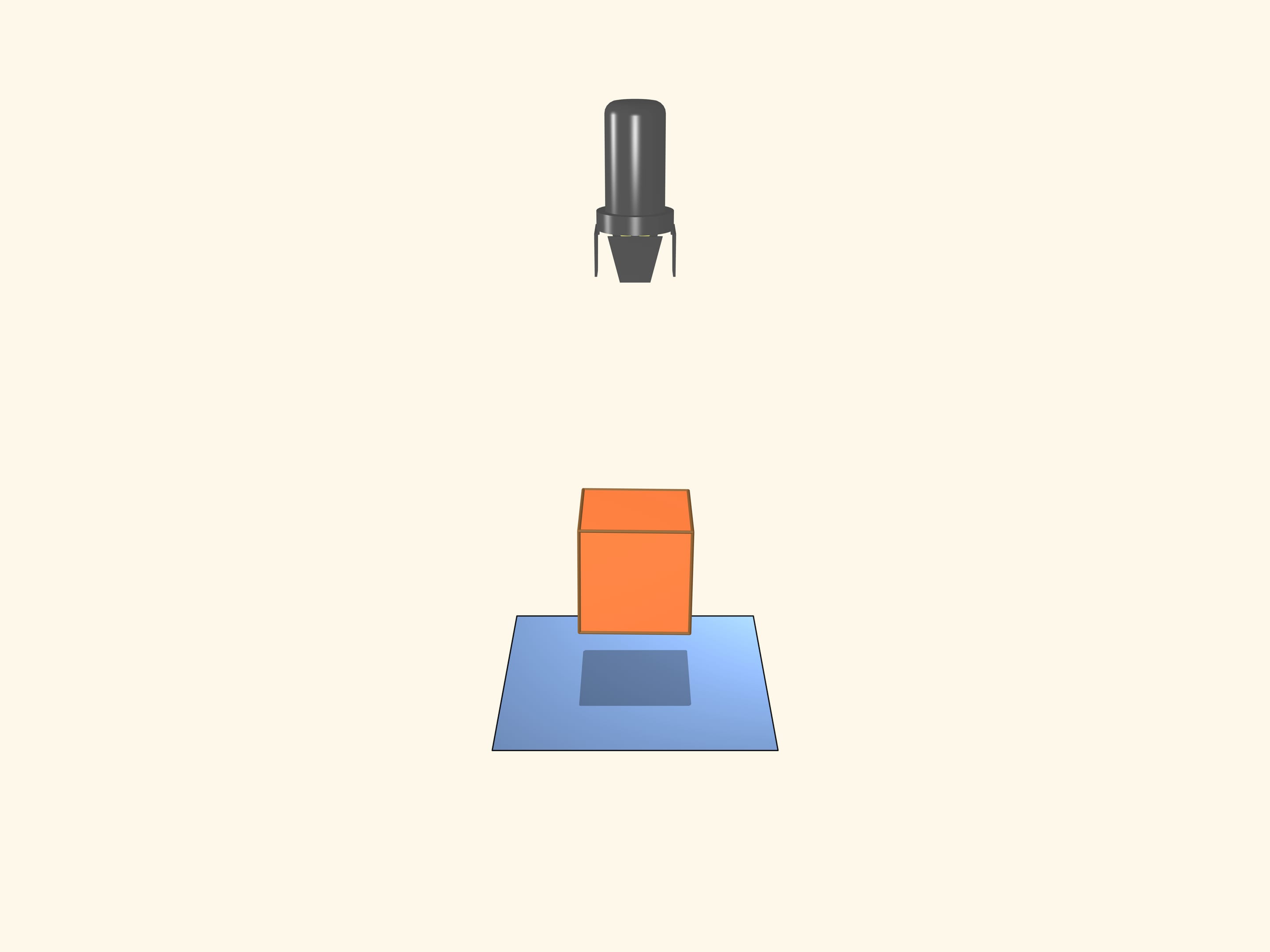
Accendiamo il proiettore e poniamo un oggetto davanti allo schermo. L’ombra proiettata è un quadrato. Siamo sicuri che l’oggetto sia un cubo?

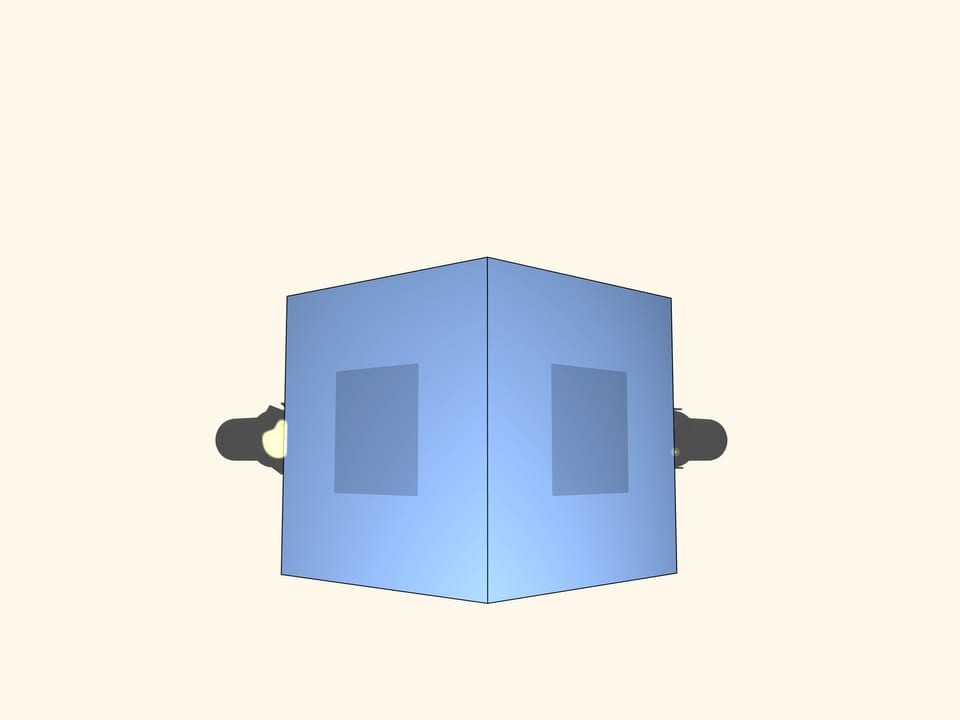
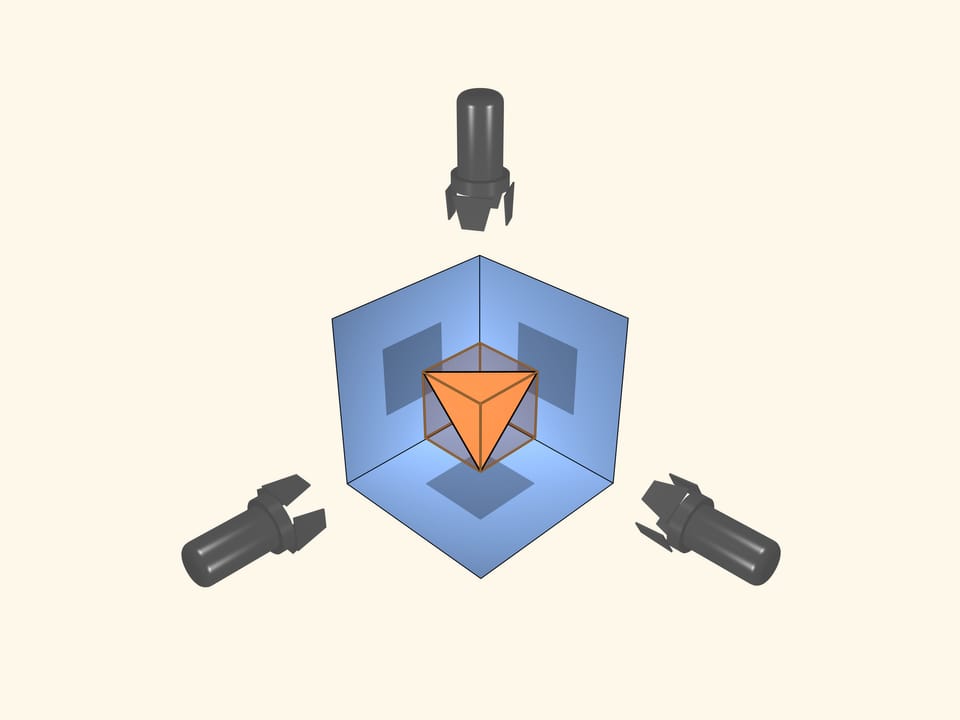
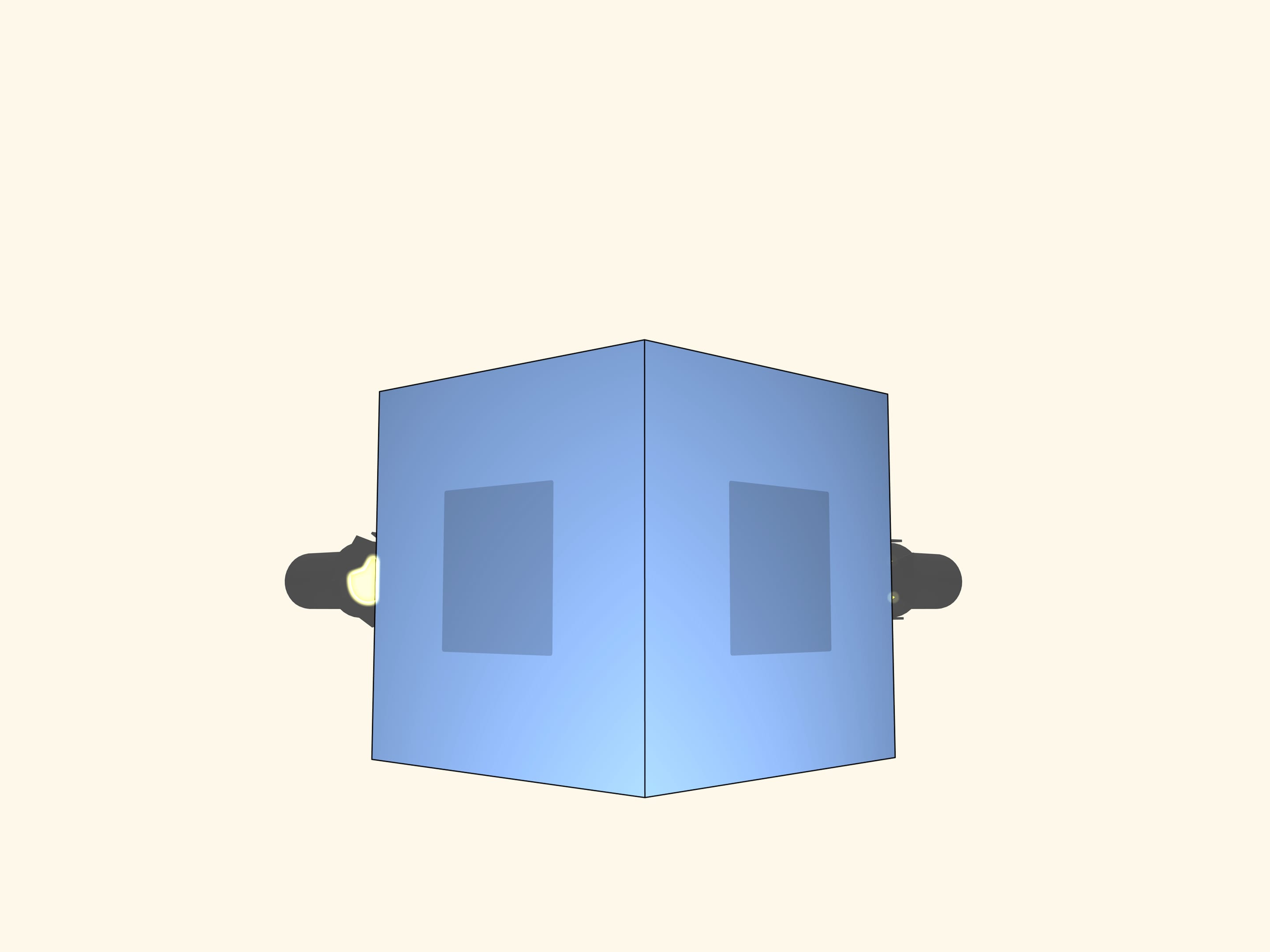
Aggiungiamo un proiettore con uno schermo in una direzione perpendicolare alla direzione del primo proiettore. Ora vediamo che due proiezioni (perpendicolari) sono dei quadrati. Solo un cubo può fare queste ombre?

E se tre proiezioni ortogonali sono dei quadrati? Esiste un oggetto diverso dal cubo, che ha queste stesse proiezioni ortogonali?

È facile inventare degli oggetti non convessi, per esempio un cubo con dei buchi, che hanno tali ombre. Ma se si considera il problema limitandosi a degli oggetti convessi, o anche all’ insieme molto più ristretto dei poliedri regolari?

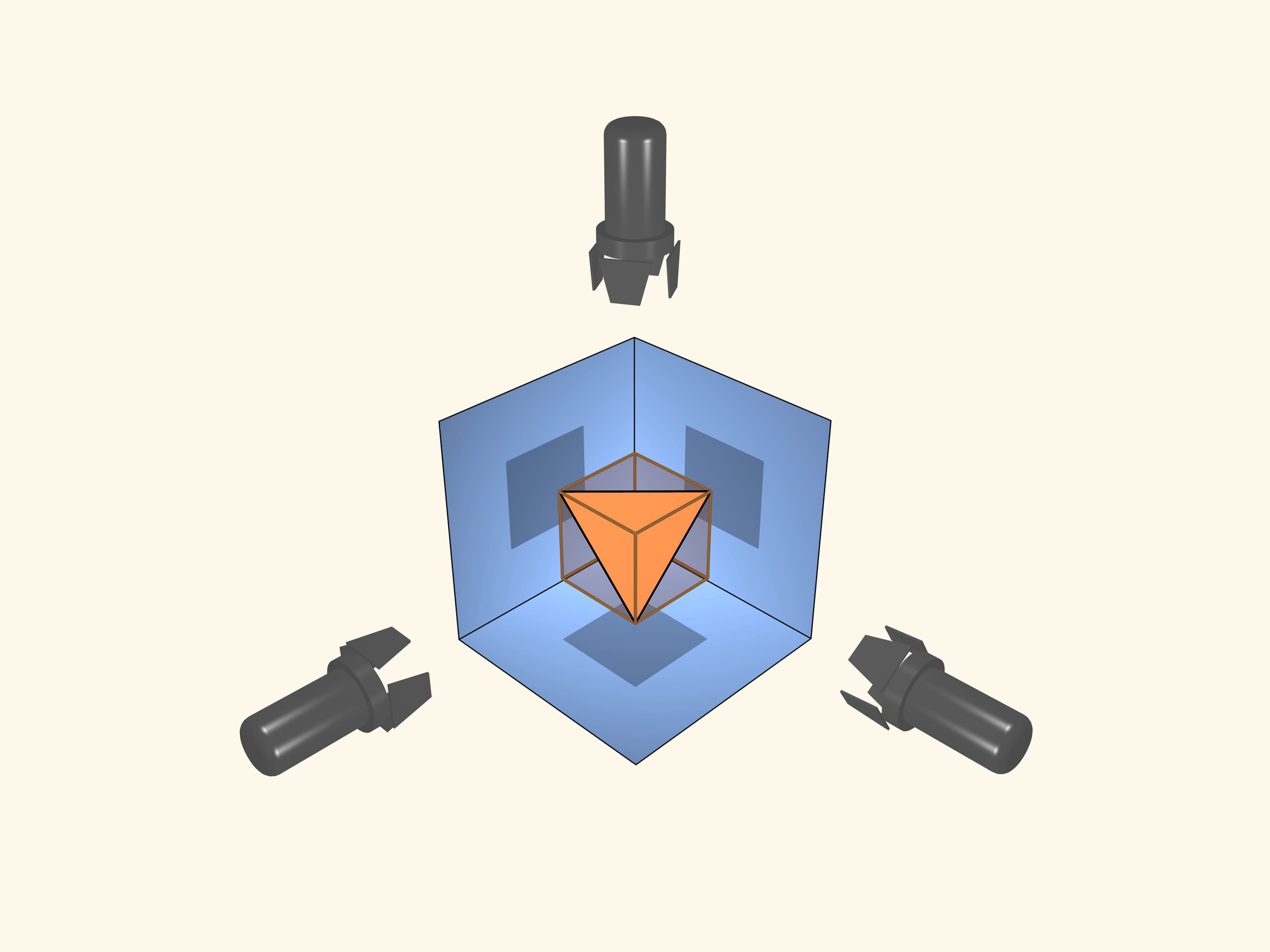
Avviene proprio che esiste un poliedro regolare, diverso dal cubo, che ha la stessa ombra di forma quadrata del cubo in tre direzioni perpendicolari.

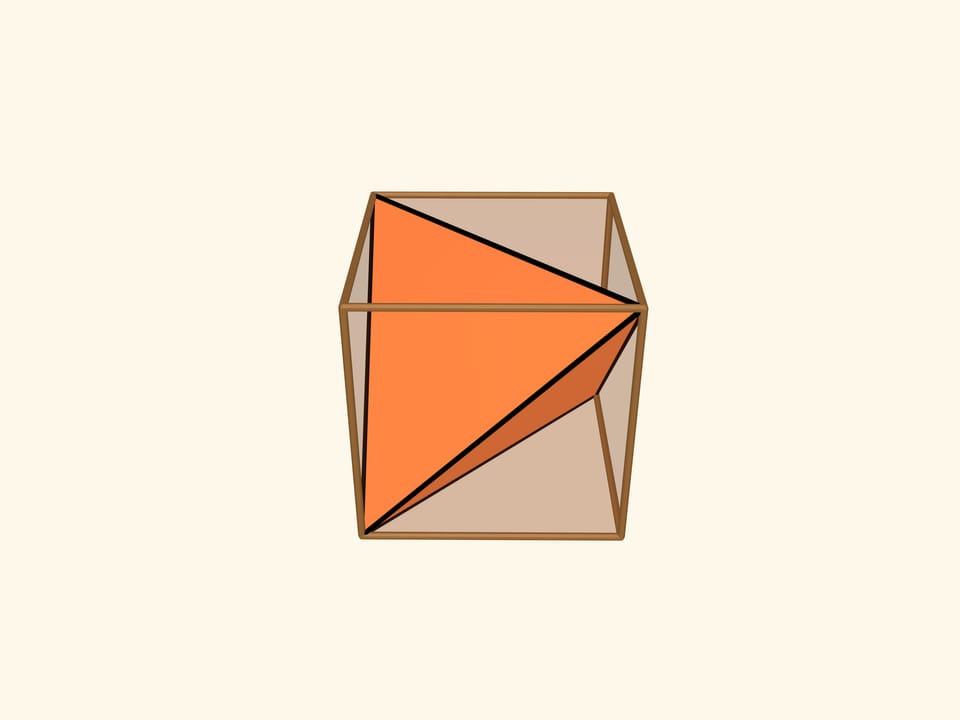
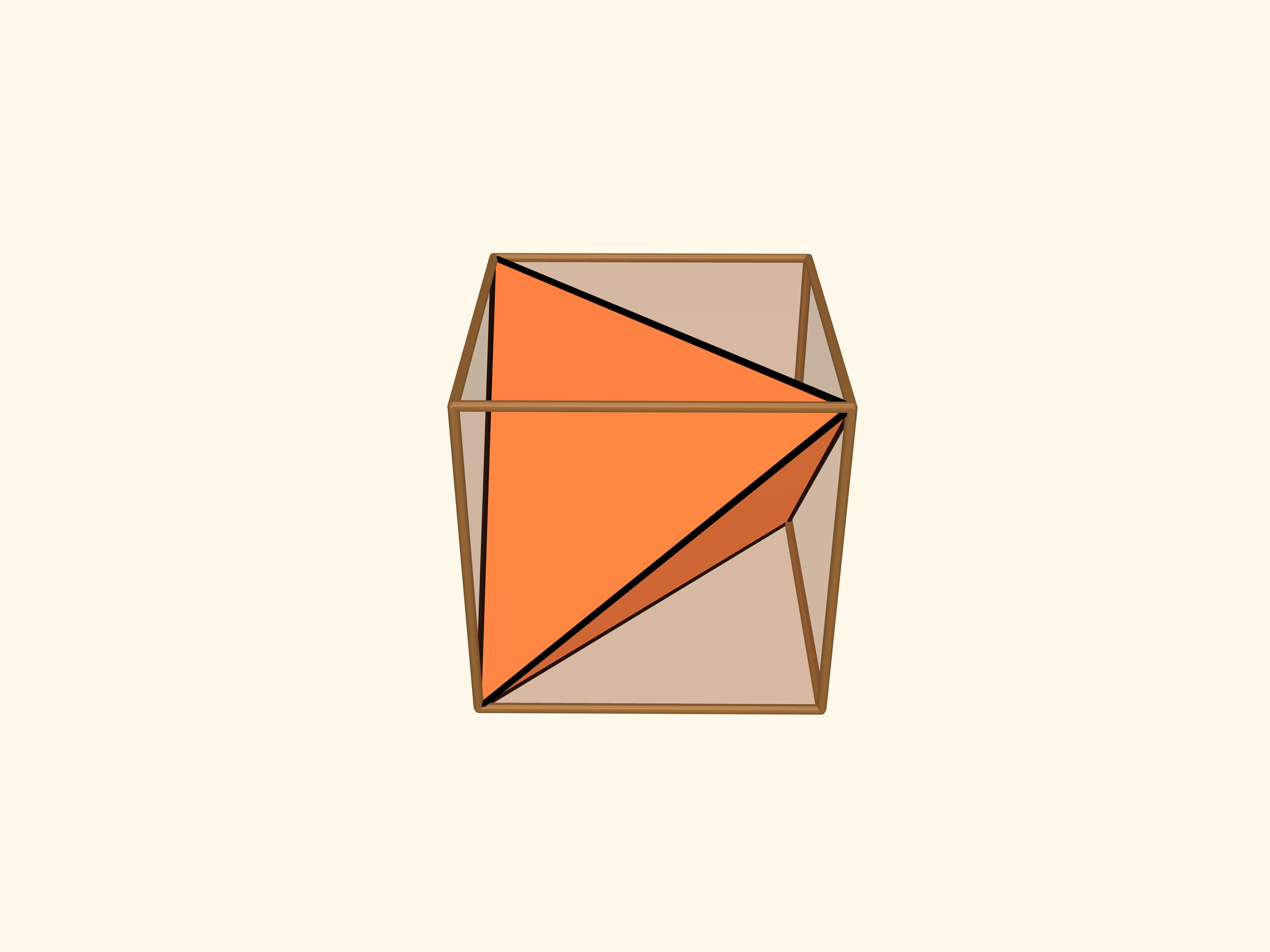
Infatti, in un cubo si può iscrivere un tetraedro regolare: quattro vertici del tetraedro coincidono con quattro degli otto vertici del cubo. I sei spigoli del tetraedro coincidono con le diagonali delle sei facce quadrate del cubo e di conseguenza saranno tutti uguali.

Se si guarda il cubo perpendicolarmente a una faccia, allora il tetraedro regolare “occupa” tutta la proiezione di quella faccia.

Questo significa che se il cubo è messo in modo tale che tre delle sue proiezioni sono dei quadrati, cioè gli schermi sono paralleli alle facce del cubo, allora anche il tetraedro regolare, che è inscritto nel cubo, farà le stesse ombre, ossia tre quadrati.