Faremo delle misurazioni. Ma, prima di misurare qualcosa, bisogna sempre definire con quale unità di misura si farà la misurazione. I ragazzi russi ricordano una canzone che diceva: “Ma io in ‘pappagalli’ sono molto più alto! ”
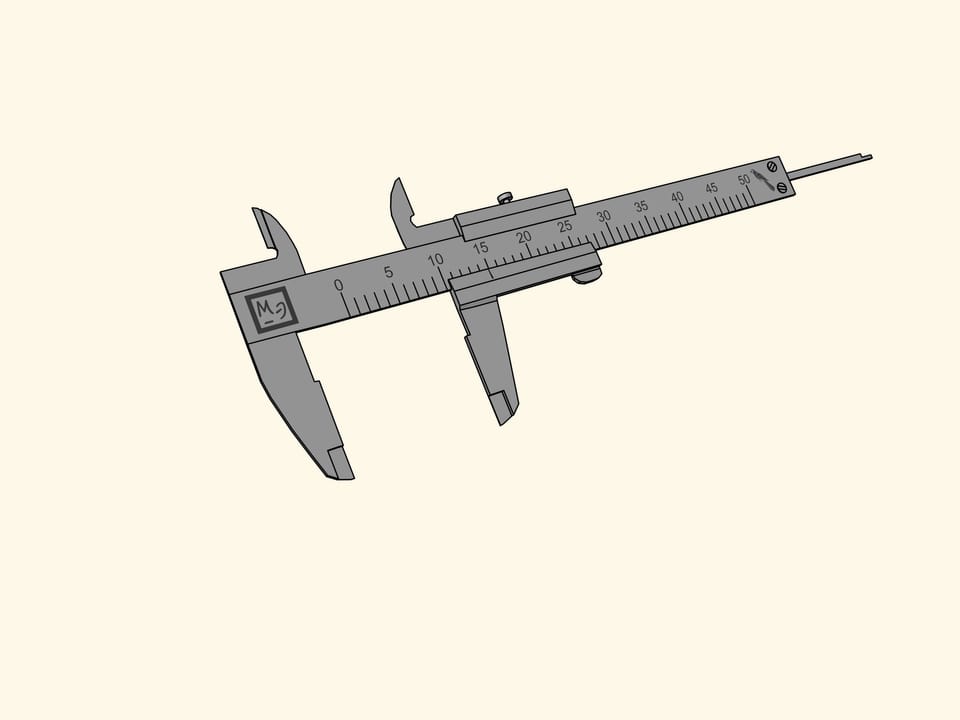
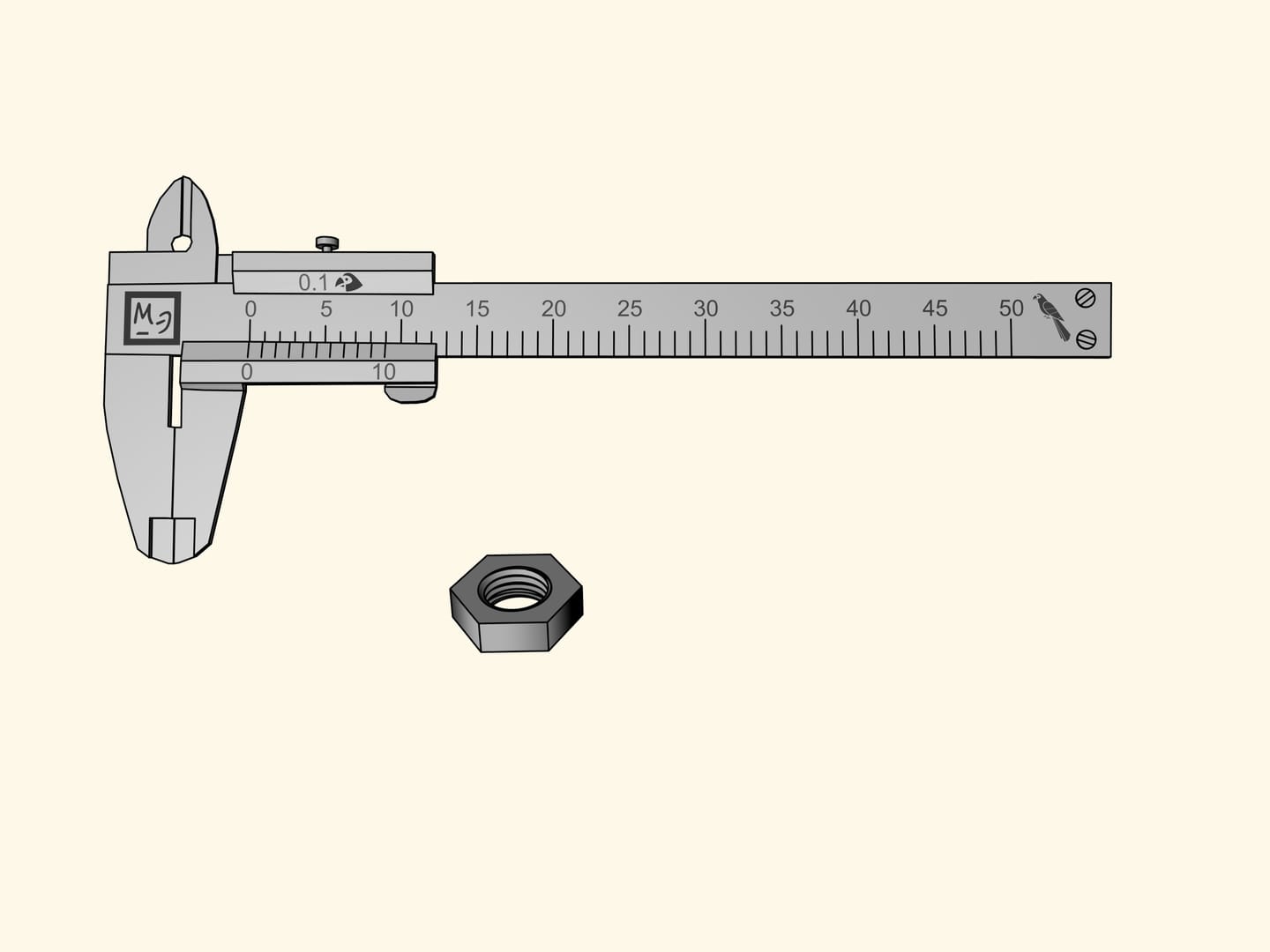
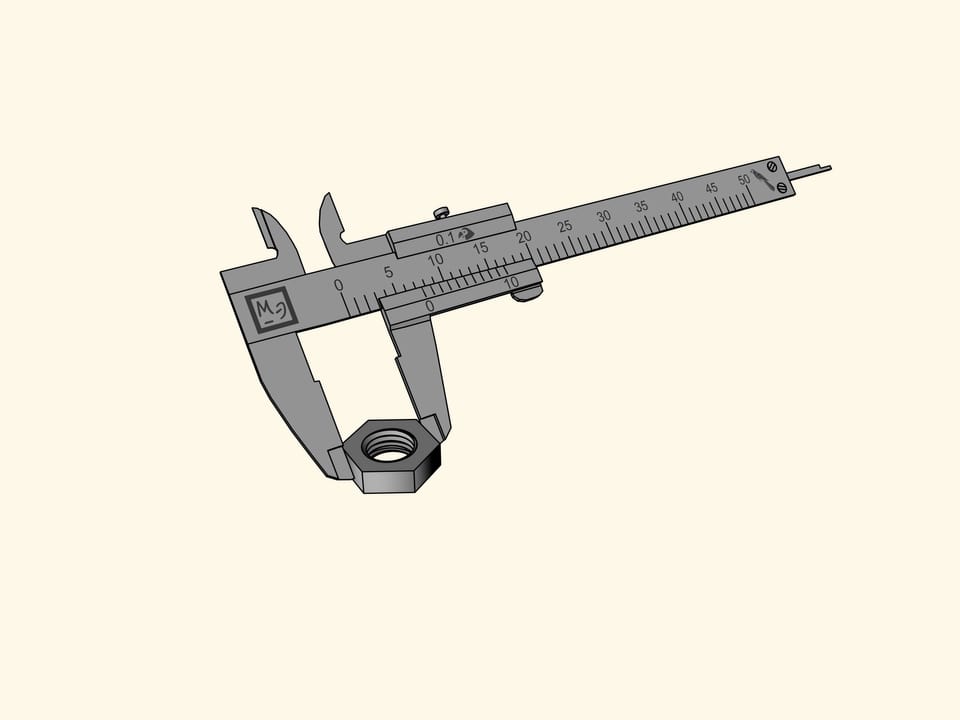
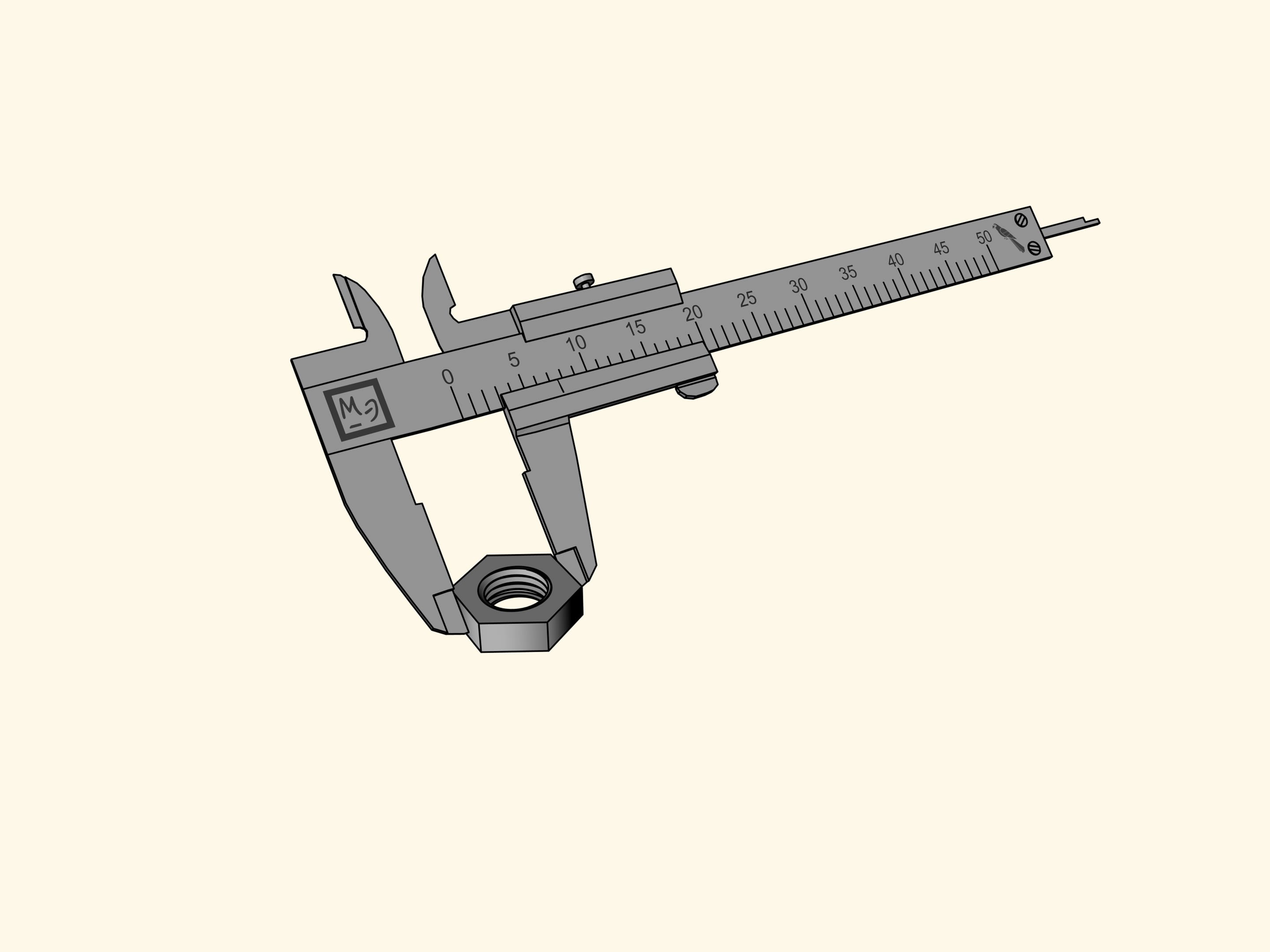
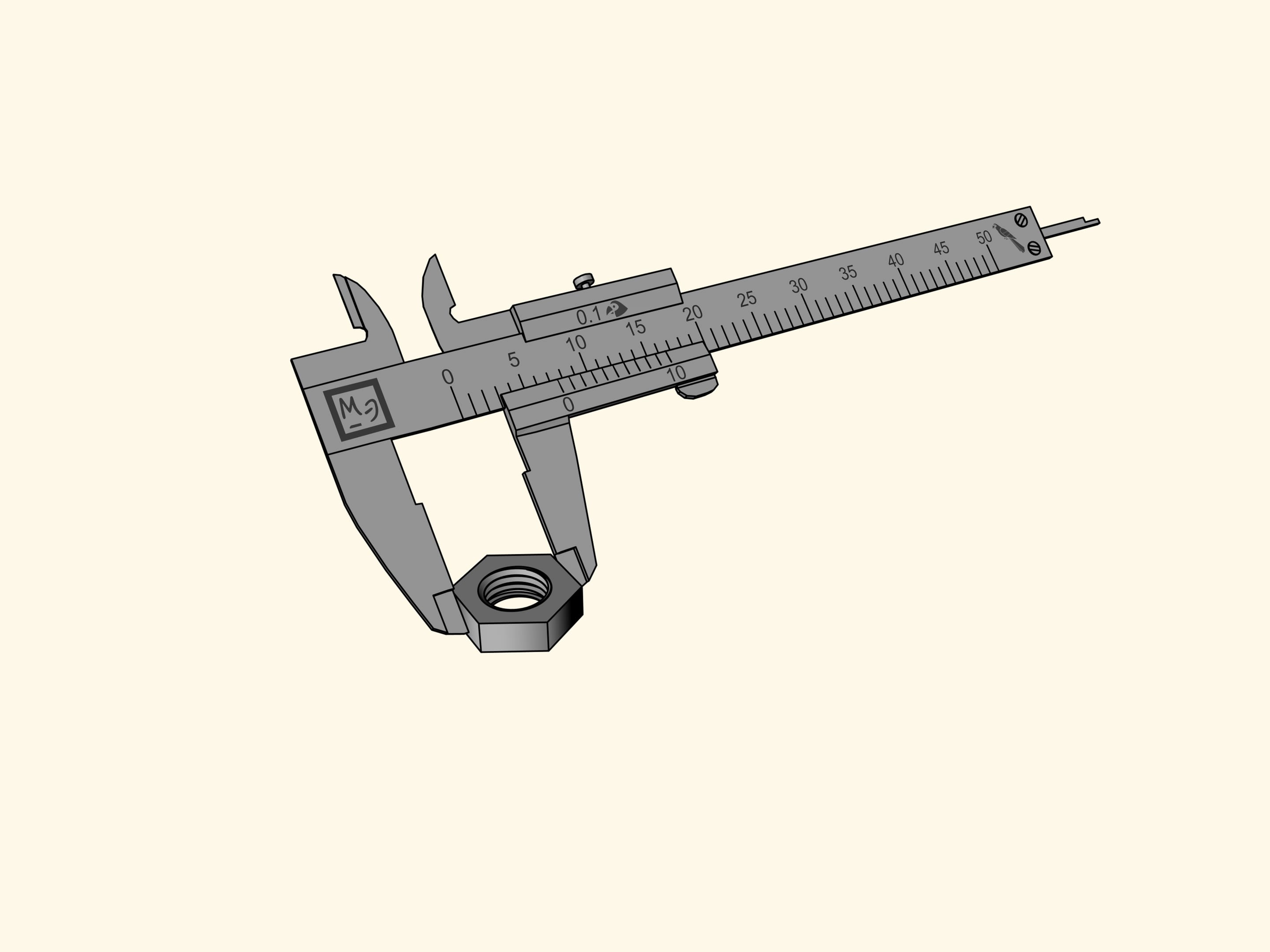
Come si misura ‘in pappagalli’ col calibro a corsoio? Le aste che si trovano al di sotto della barra graduata principale servono per le misure esterne, quando occorre misurare, per esempio, il diametro esterno di un tubo. Le aste per le misure interne, utilizzate per misurare, per esempio, il diametro interno di un tubo, si trovano al di sopra della barra. Infine, c’è una ‘coda’ che sporge in fondo alla barra, e serve per misurare la profondità, per esempio, di un foro. Queste tre parti sono fissate a una barretta scorrevole che misura 15 pappagalli.
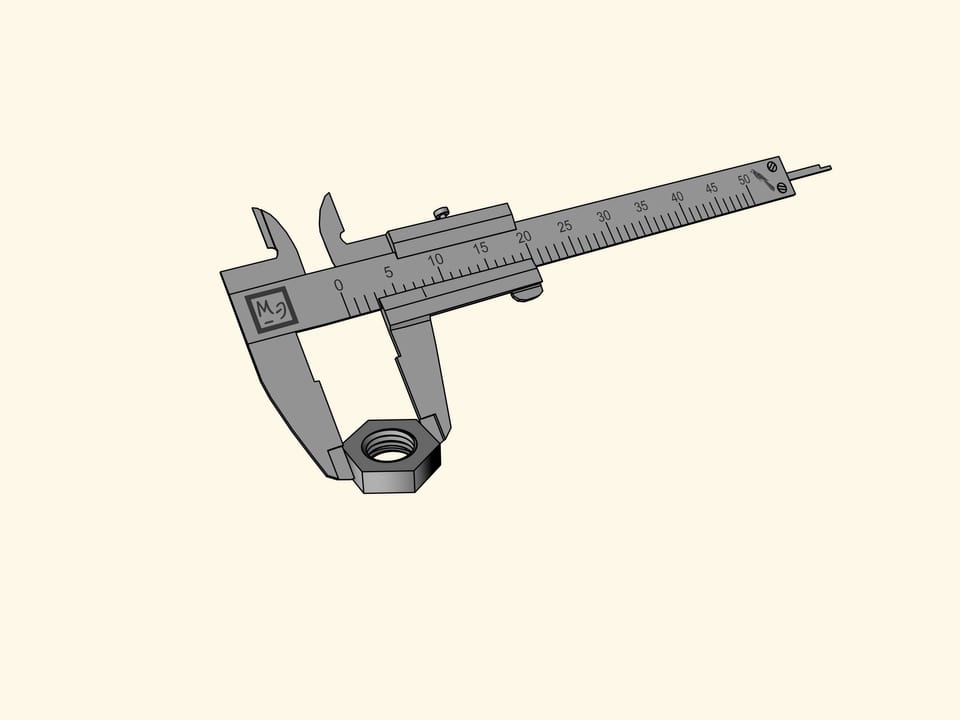
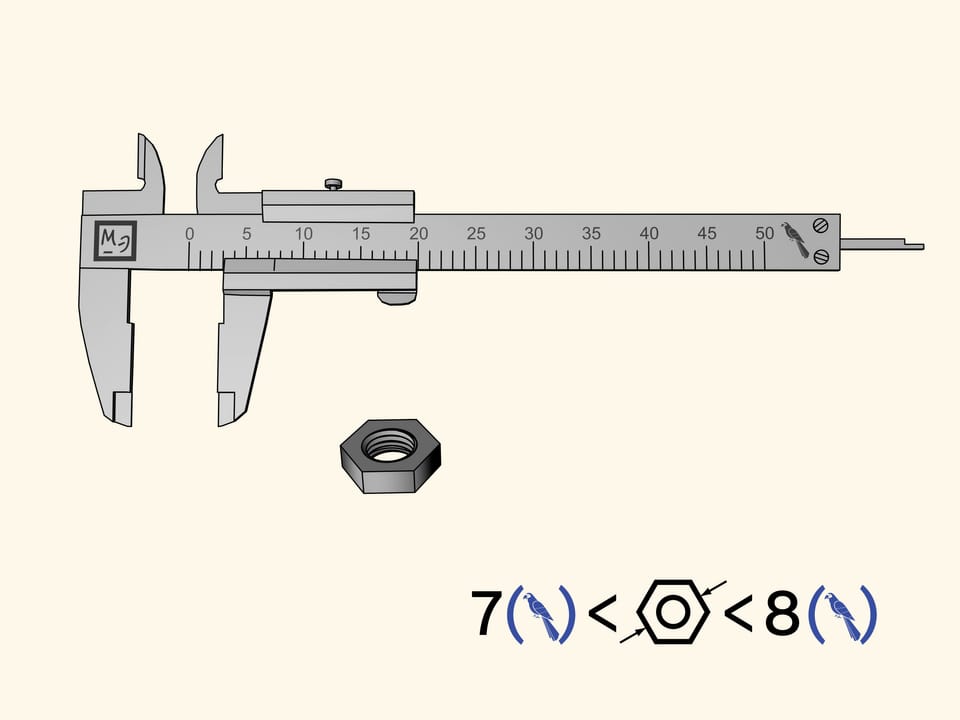
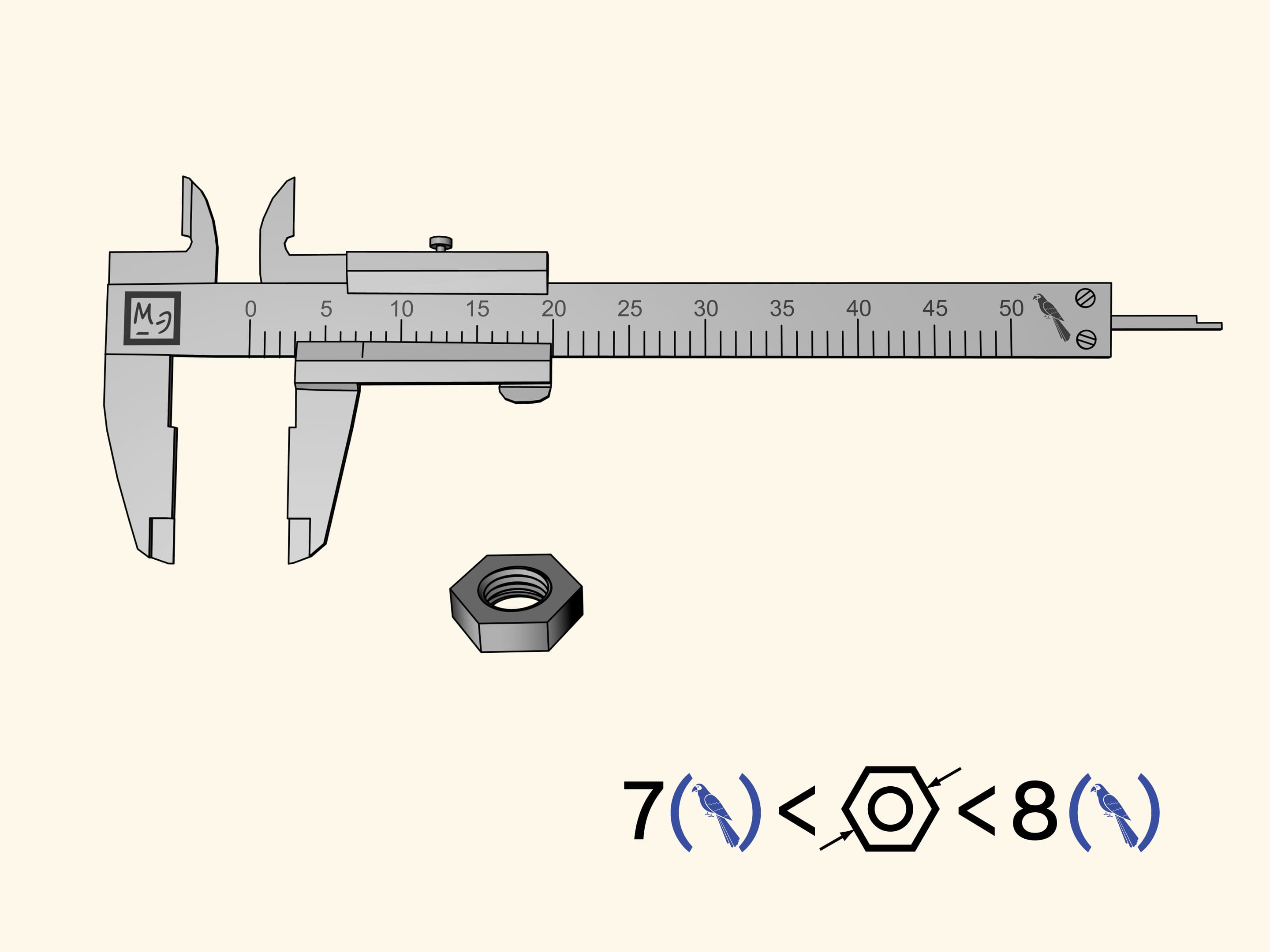
Misuriamo un dado esagonale. Sfortunatamente, la tacca di riferimento (lo zero) sulla barretta scorrevole che mostra la grandezza del dado, è finita tra due divisioni della barra principale. Tutto quello che questa misurazione ci permette di dire è che il dado misura più di sette pappagalli, ma meno di otto. È difficile definire la sua grandezza più precisamente a occhio.
Un metodo, che non complica affatto la costruzione dello stesso calibro, ma permette di ottenere risultati più precisi, fu inventato alcuni secoli fa. Questo si limita ad aggiungere sulla barretta mobile una scala graduata supplementare, il nonio.
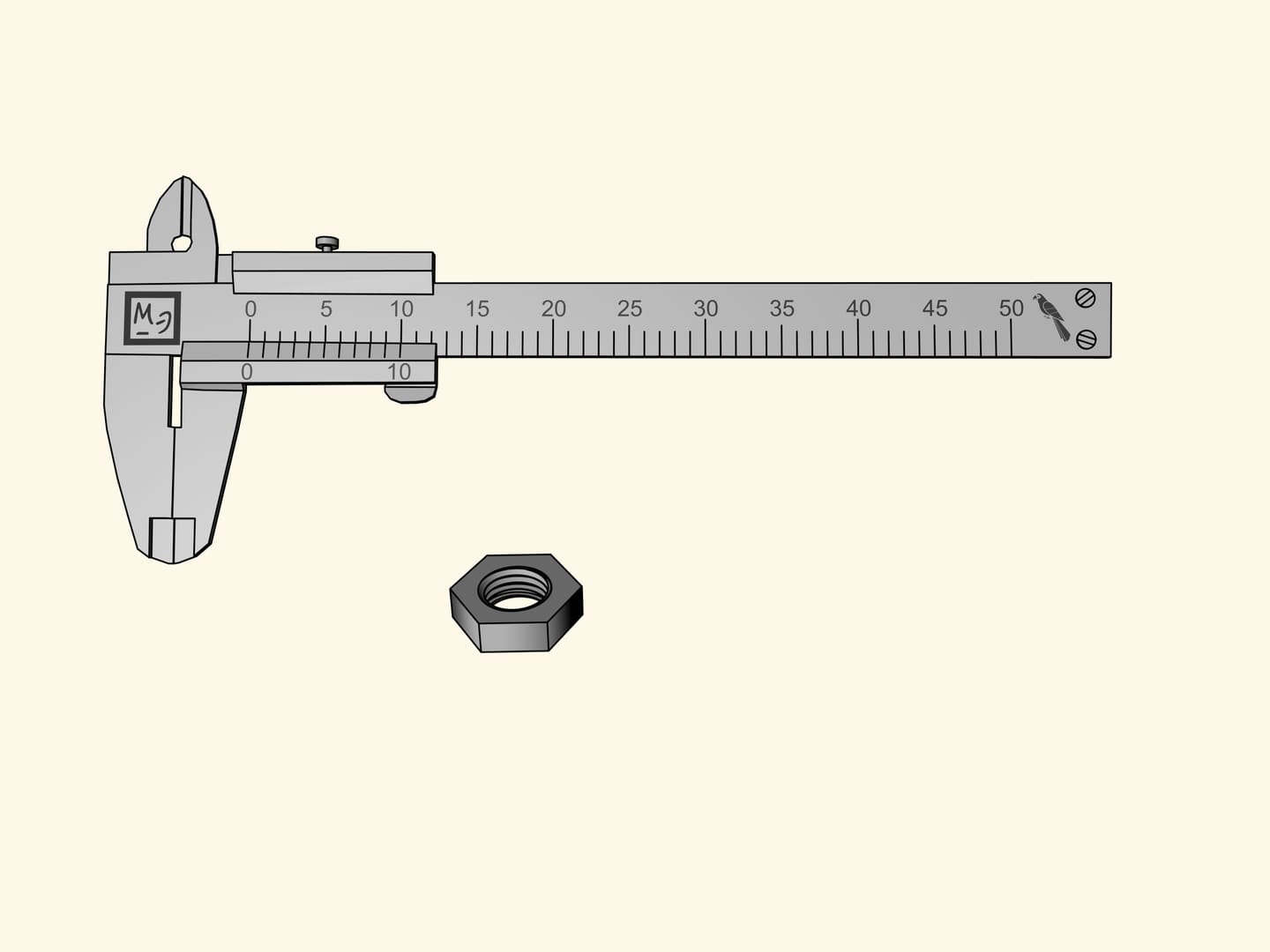
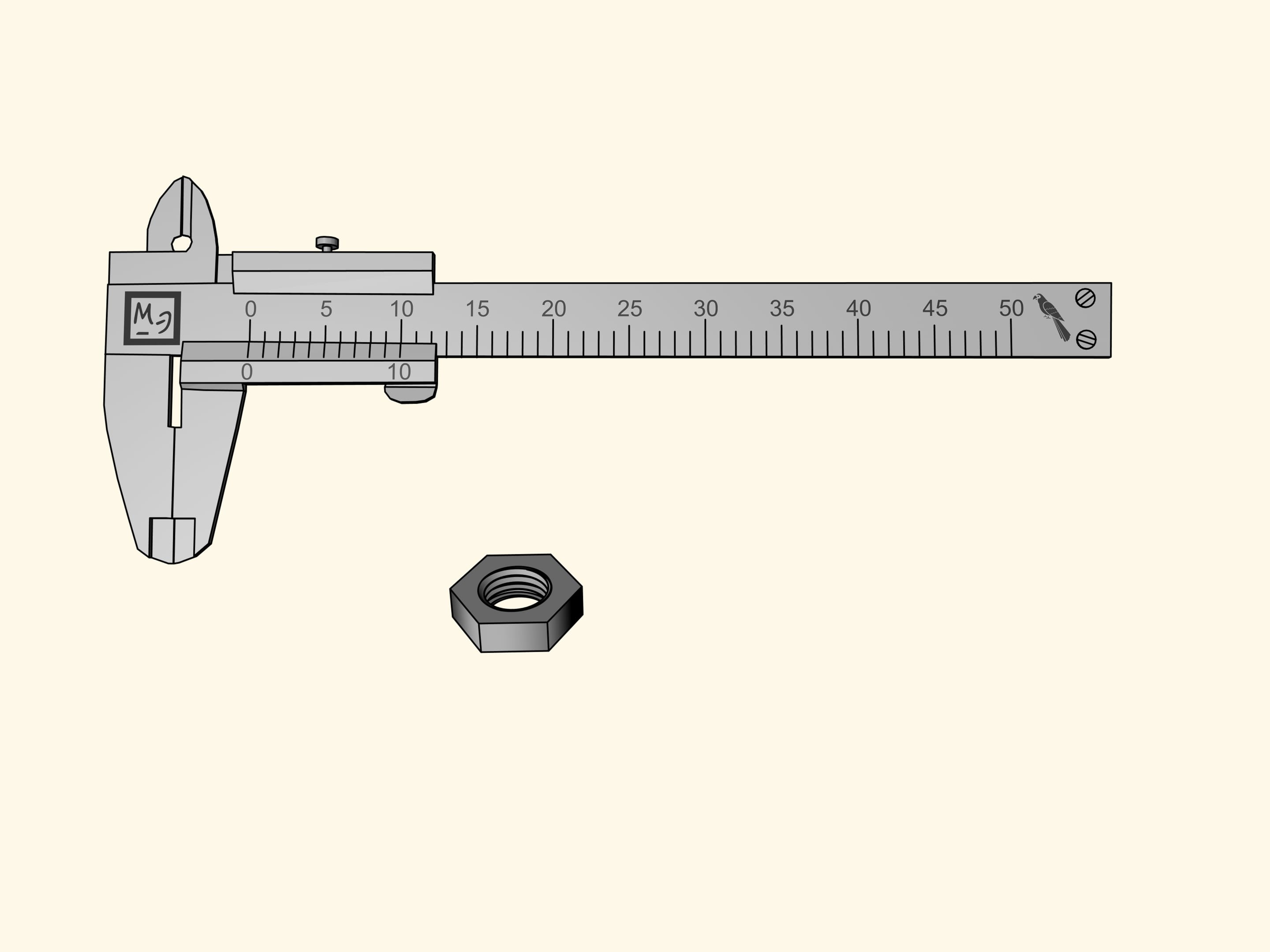
Poniamo su questa barretta mobile dieci tacche dopo lo zero che coincidono con le tacche tra 0 e 10 della scala principale. Ora comprimiamo in modo uniforme queste dieci divisioni in modo che occupino nove divisioni della scala principale. La riga costruita in questo modo si chiama nonio, in onore del matematico portoghese Pedro Nunes che la inventò. L’attuale forma fu proposta dal matematico francese Pierre Vernier, da cui prende il secondo nome di verniero.
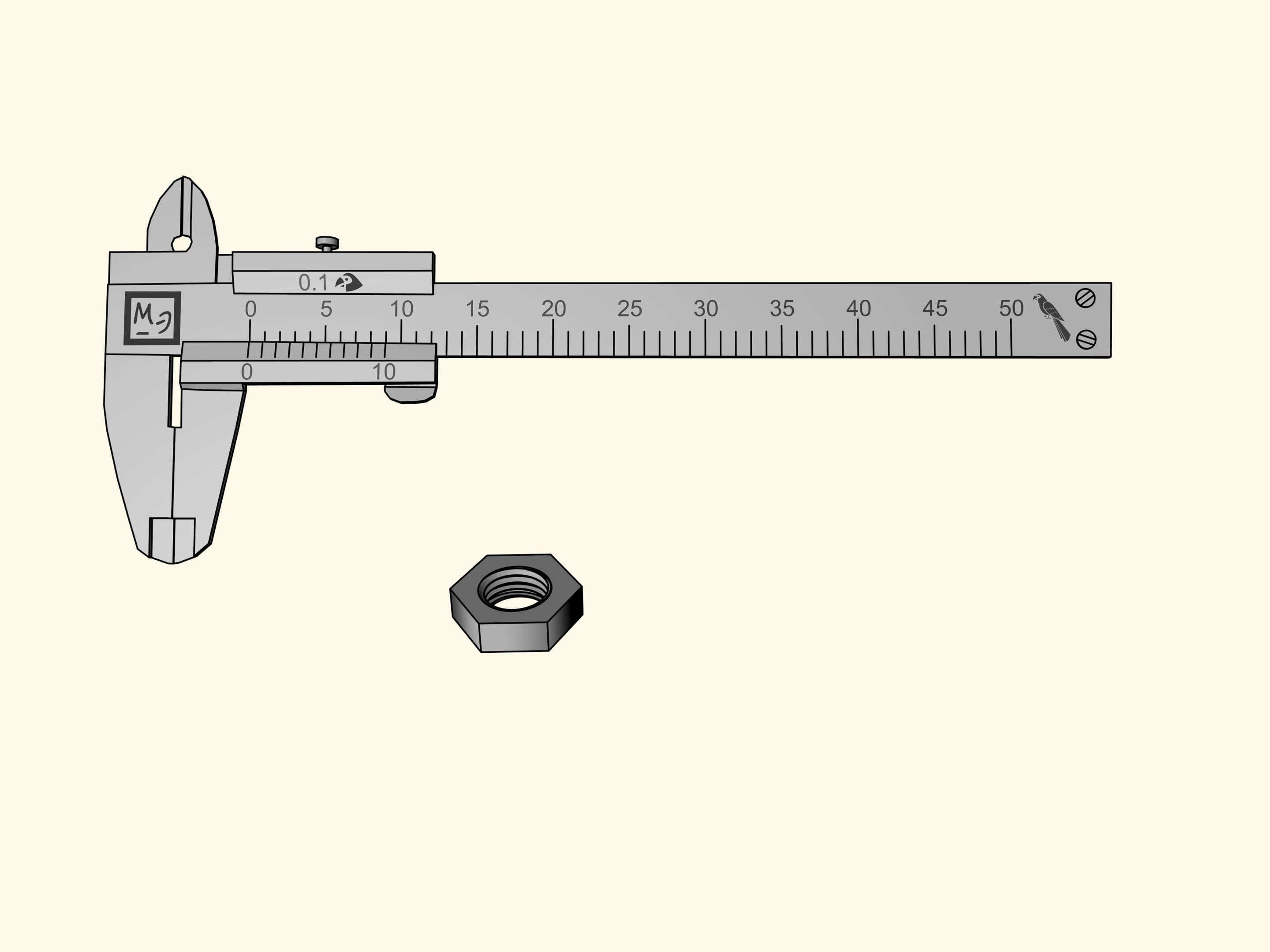
Avviene che la riga supplementare costruita in questo modo permette di misurare con la precisione di $0{,}1$ pappagalli. Ma come?
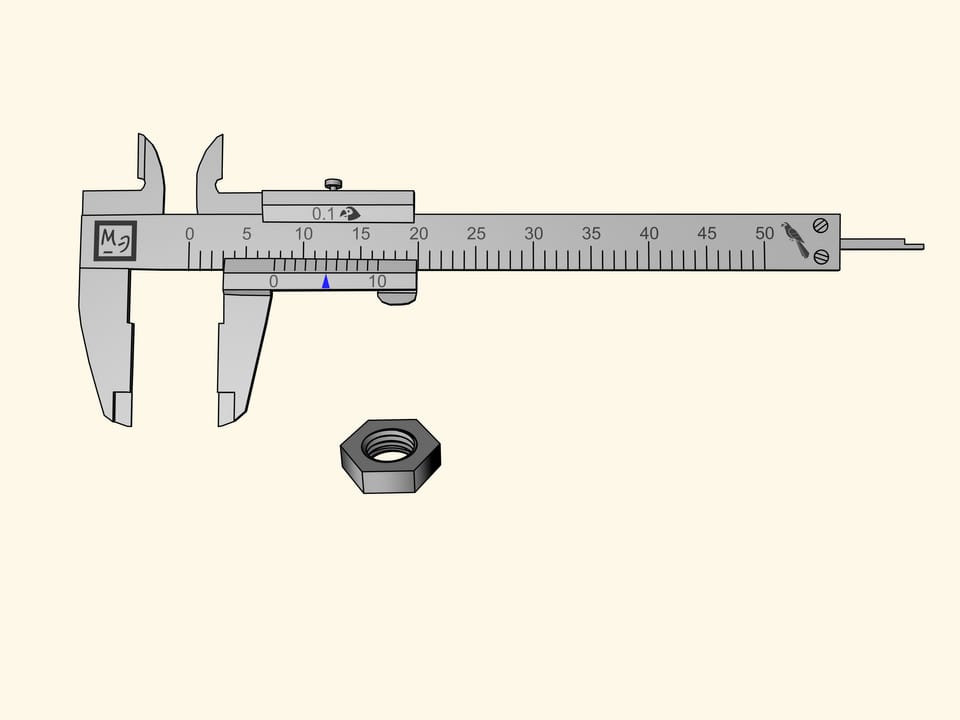
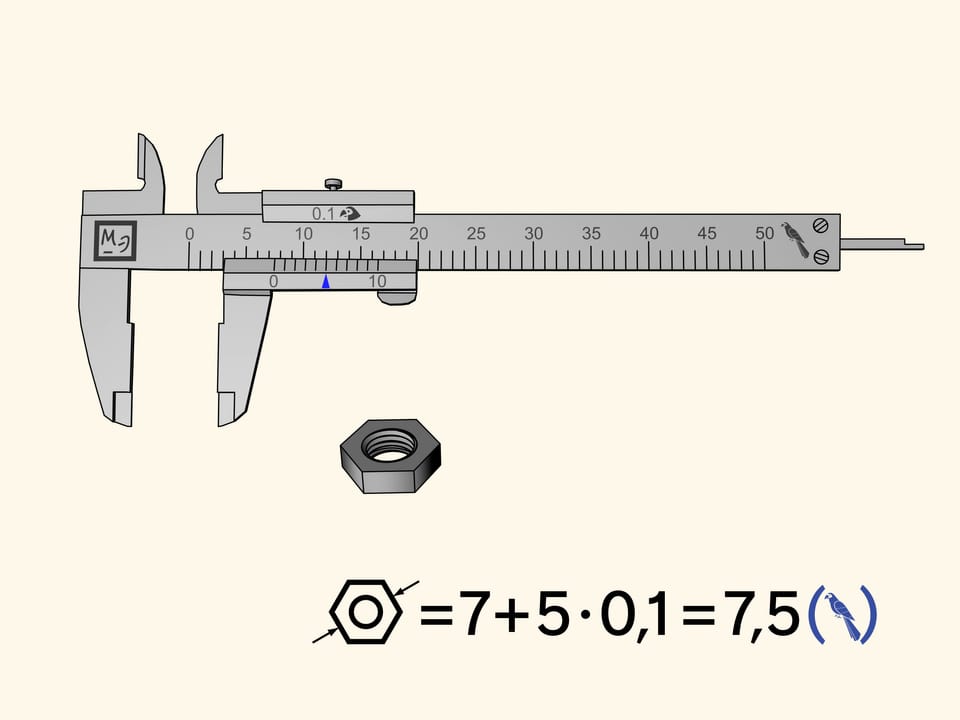
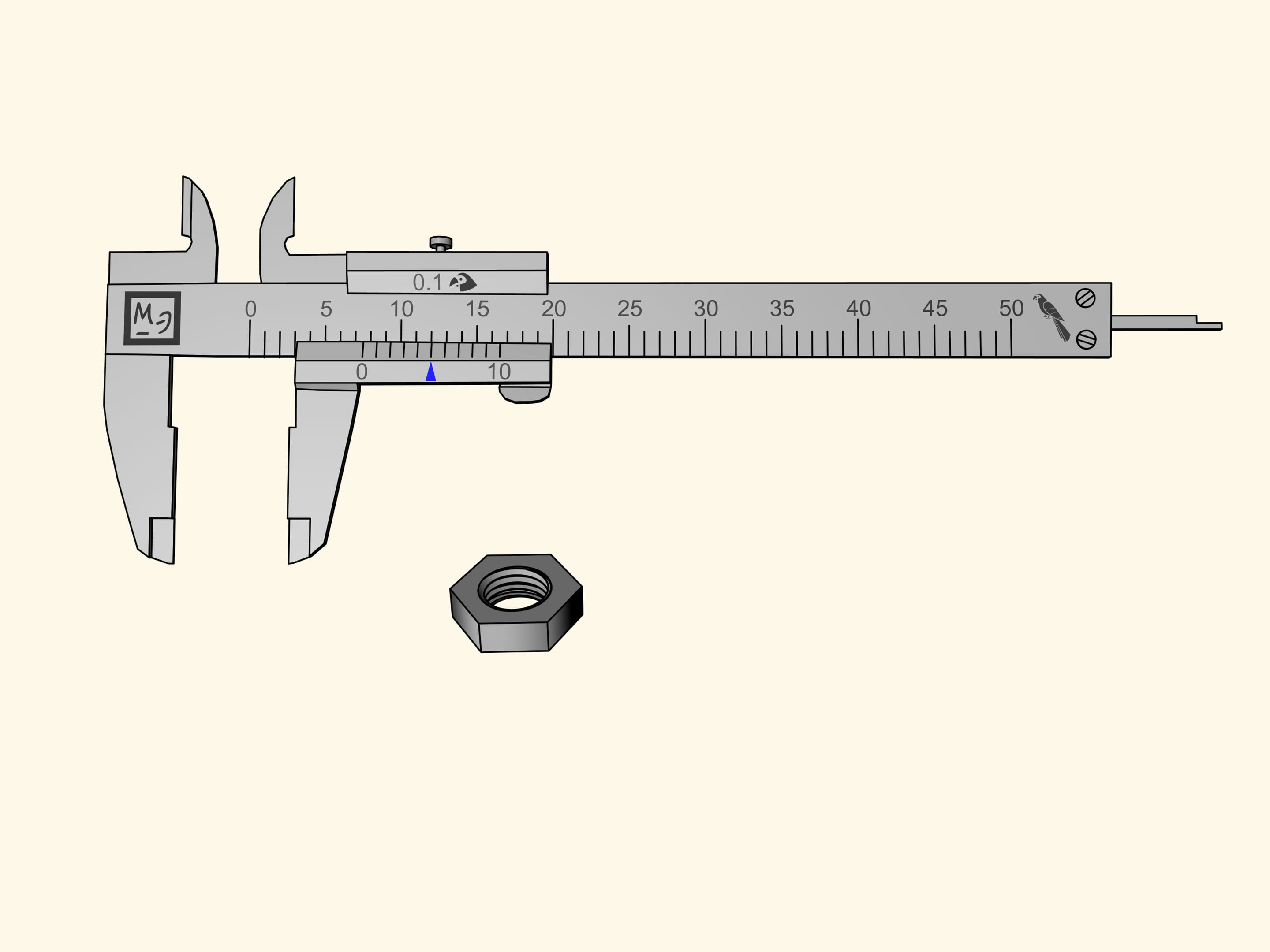
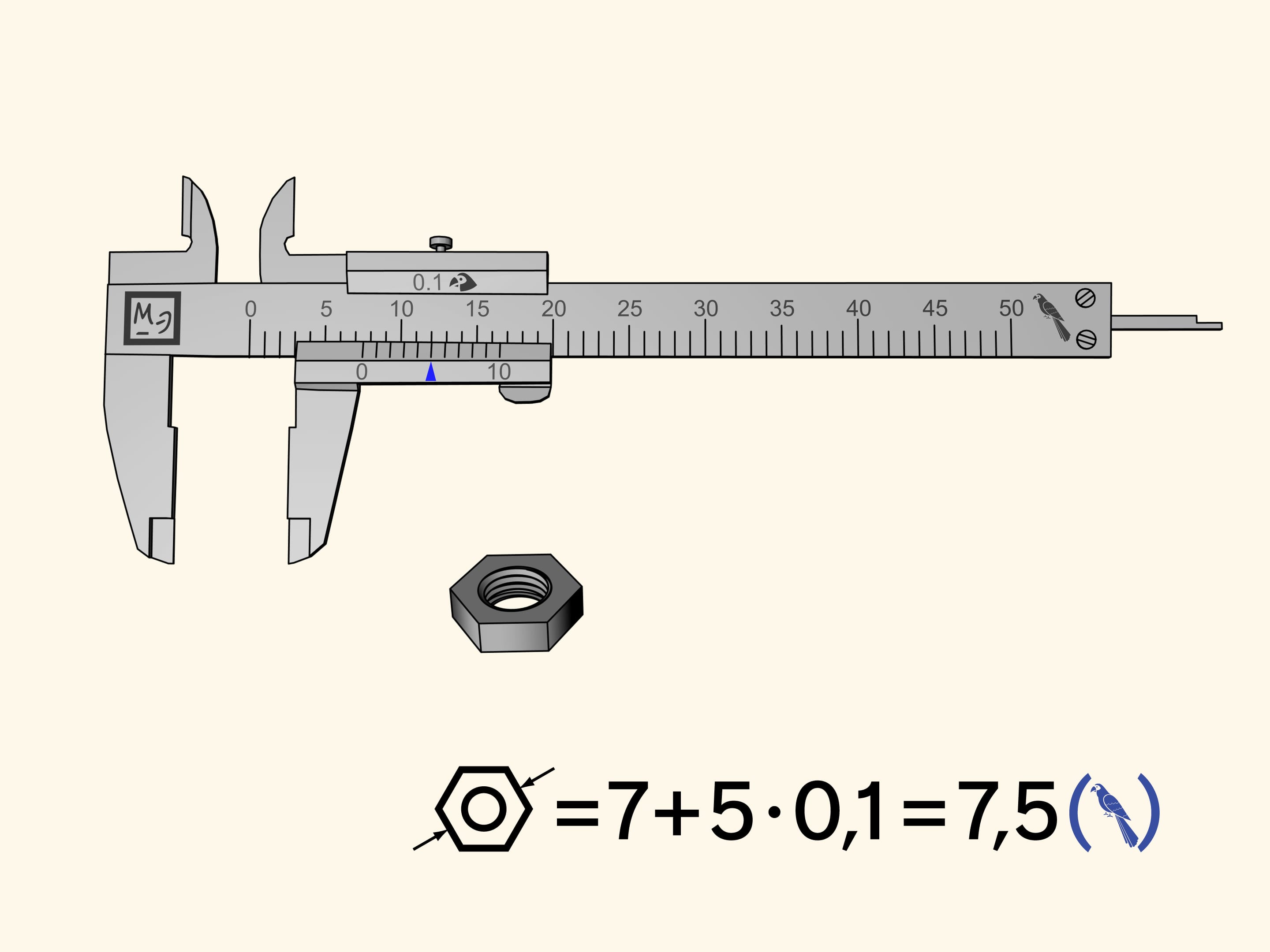
Misuriamo il dado ancora una volta. Lo zero della barretta mobile sarà, come prima, tra la settima e l’ottava divisione. Ciò significa che la nostra misura contiene sette pappagalli interi. Ora scorriamo le divisioni della riga supplementare da sinistra a destra e cerchiamo la tacca che coincide con una delle divisioni della scala principale. Nel nostro caso questo capita alla quinta tacca. Di conseguenza, la misura del dado è uguale a $7 + 5 × 0{,}1 = 7{,}5$ (pappagalli).
Spiegate matematicamente l’argomento di cui sopra. Pensate a come utilizzare la stessa idea per ottenere una maggiore precisione.