Inventare la ruota ⁠

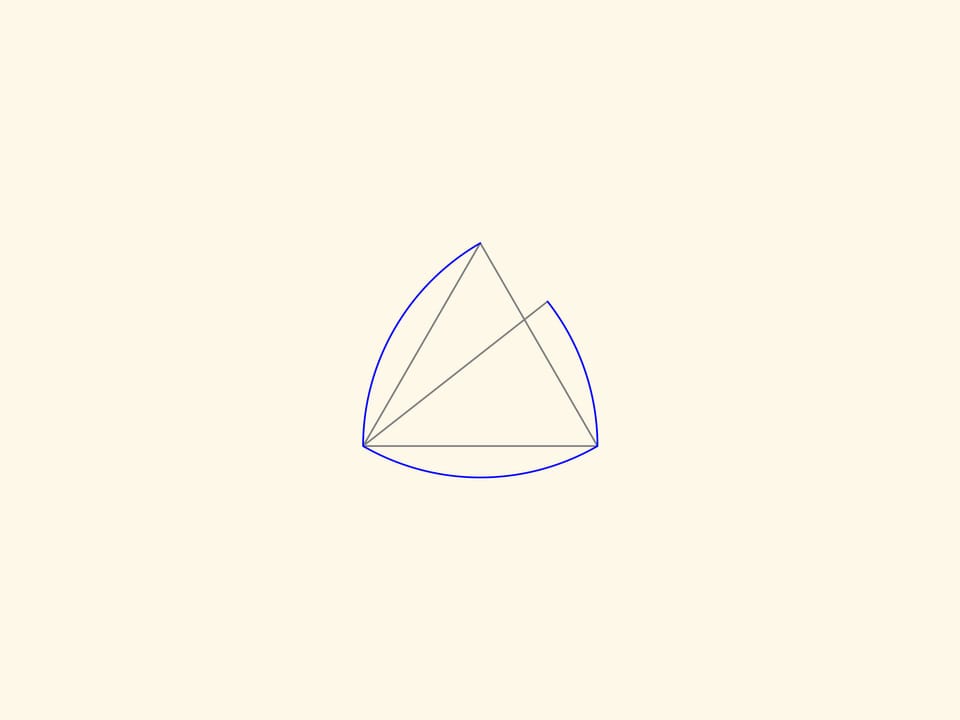
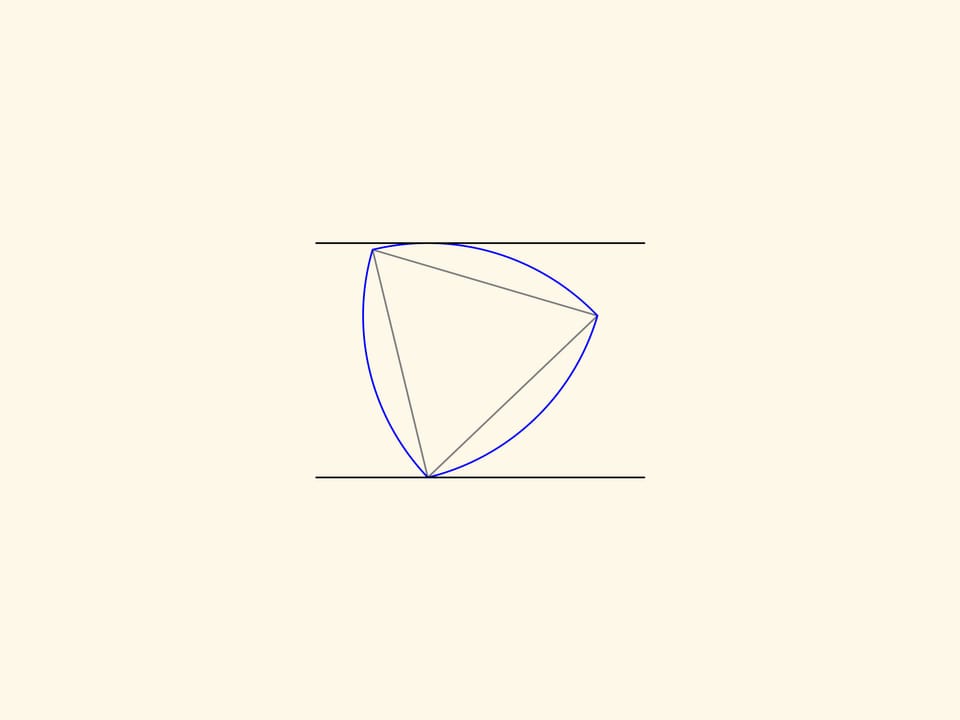
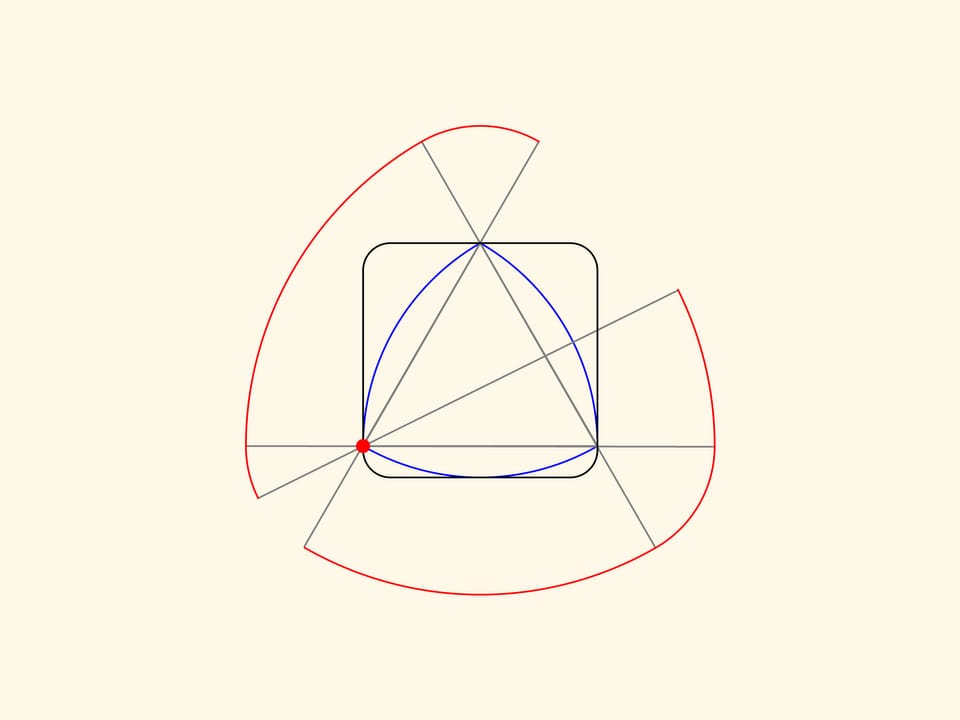
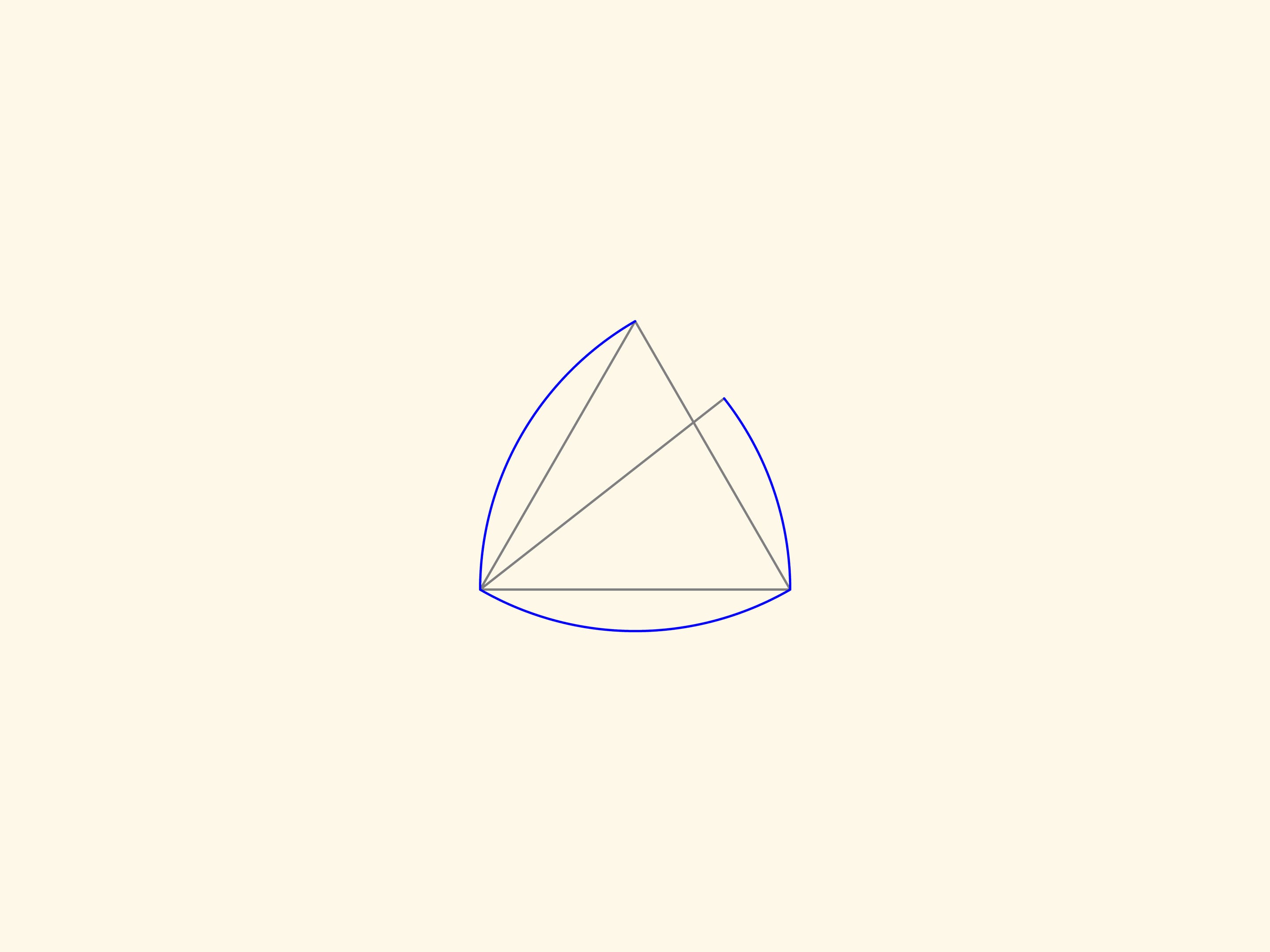
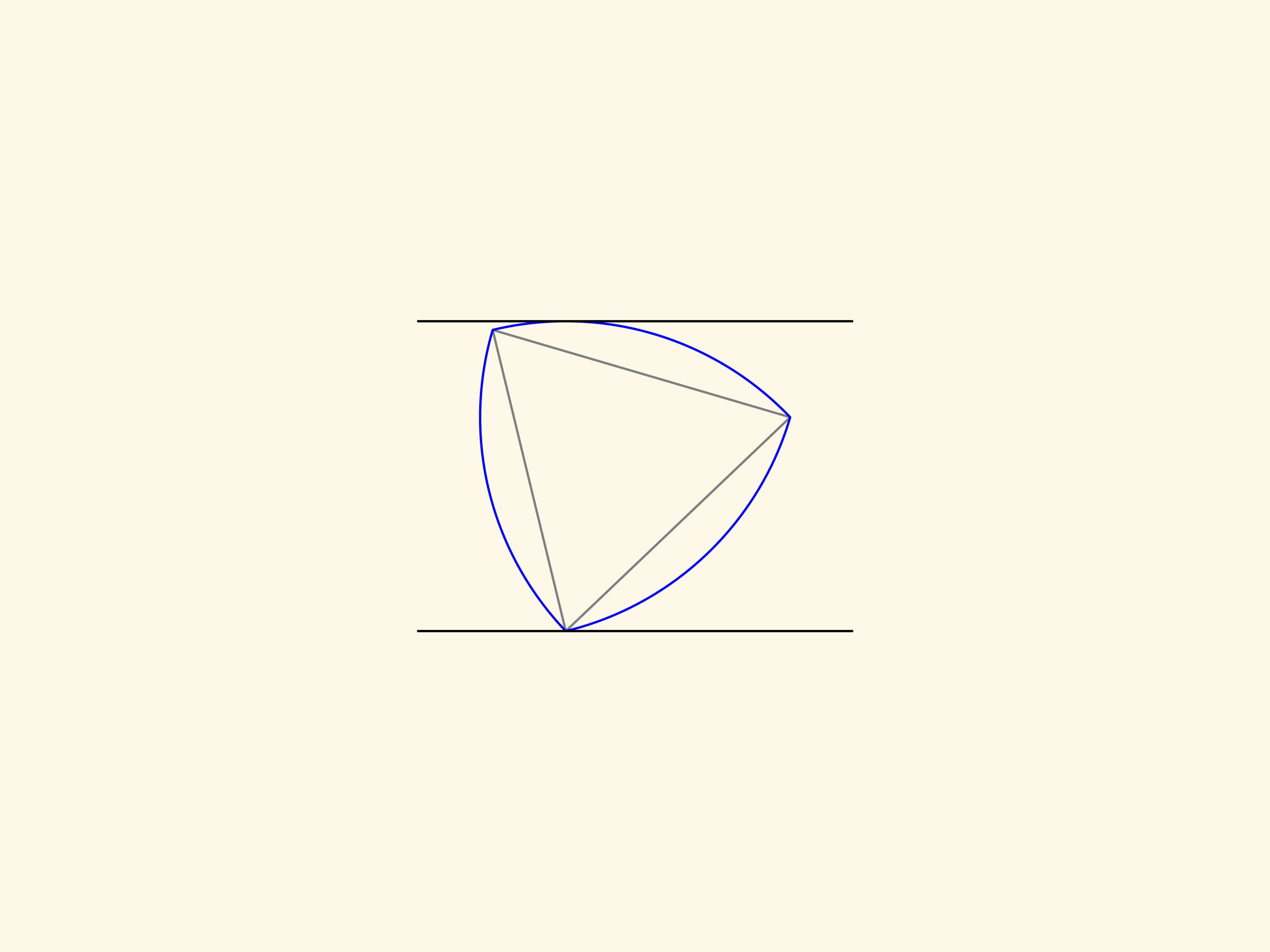
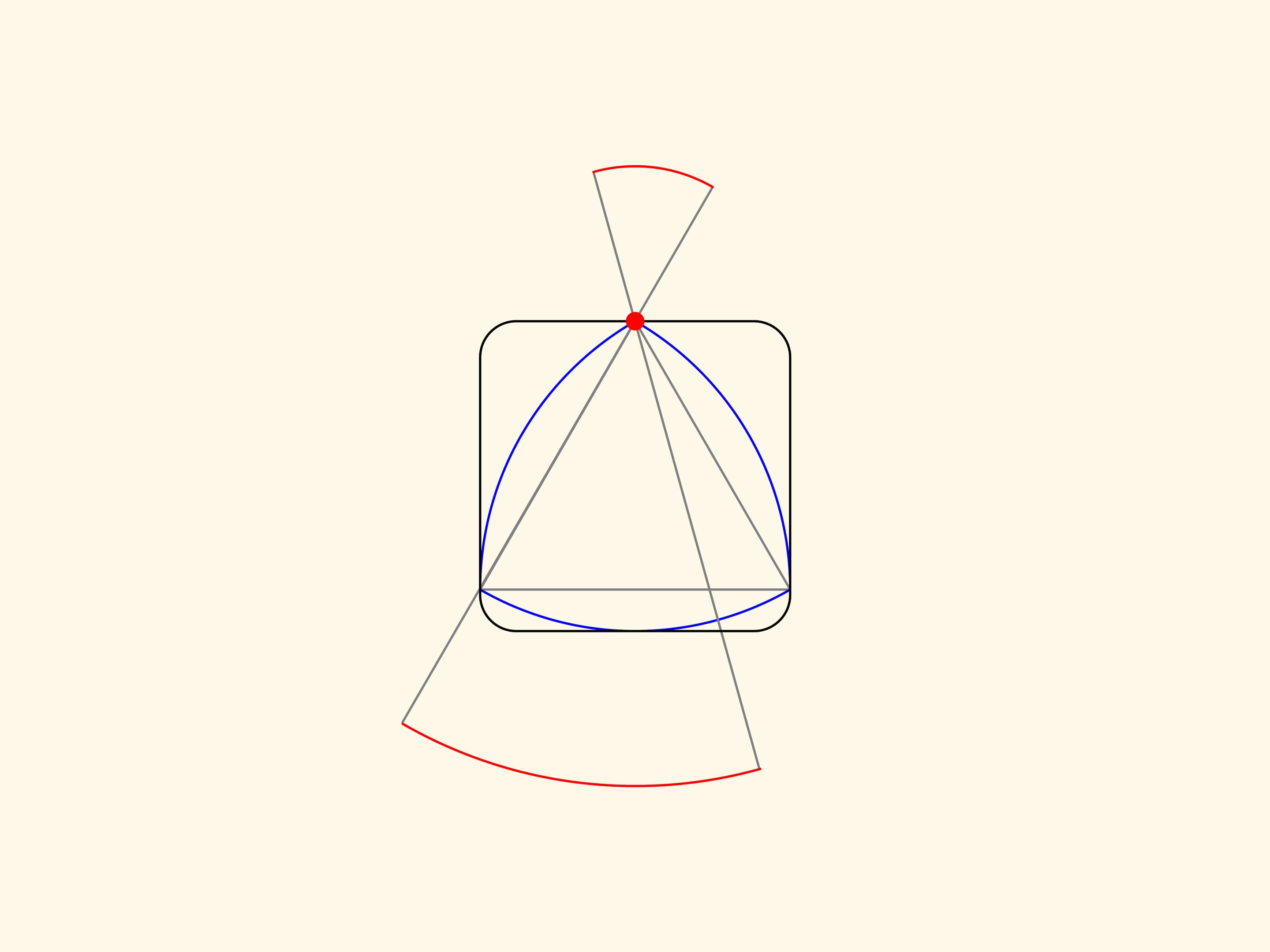
Il ⁠⁠triangolo di Reuleaux è una figura piana di larghezza costante: può essere cioè ruotato tra due linee parallele che si trovano ad una distanza fissa l’una dall’altra, restando continuamente a contatto con entrambe.

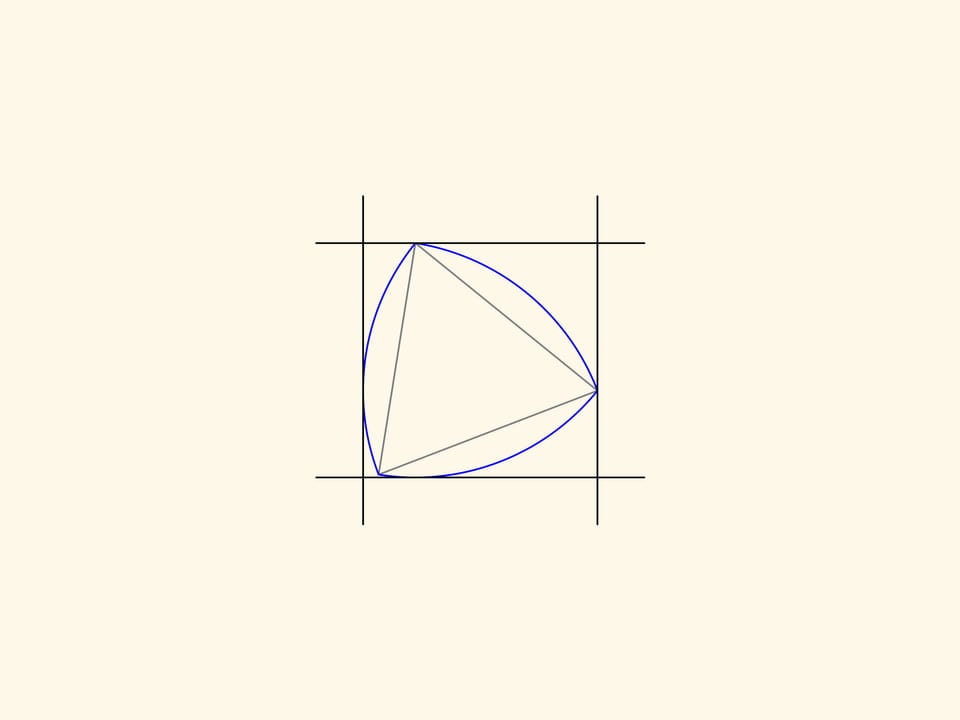
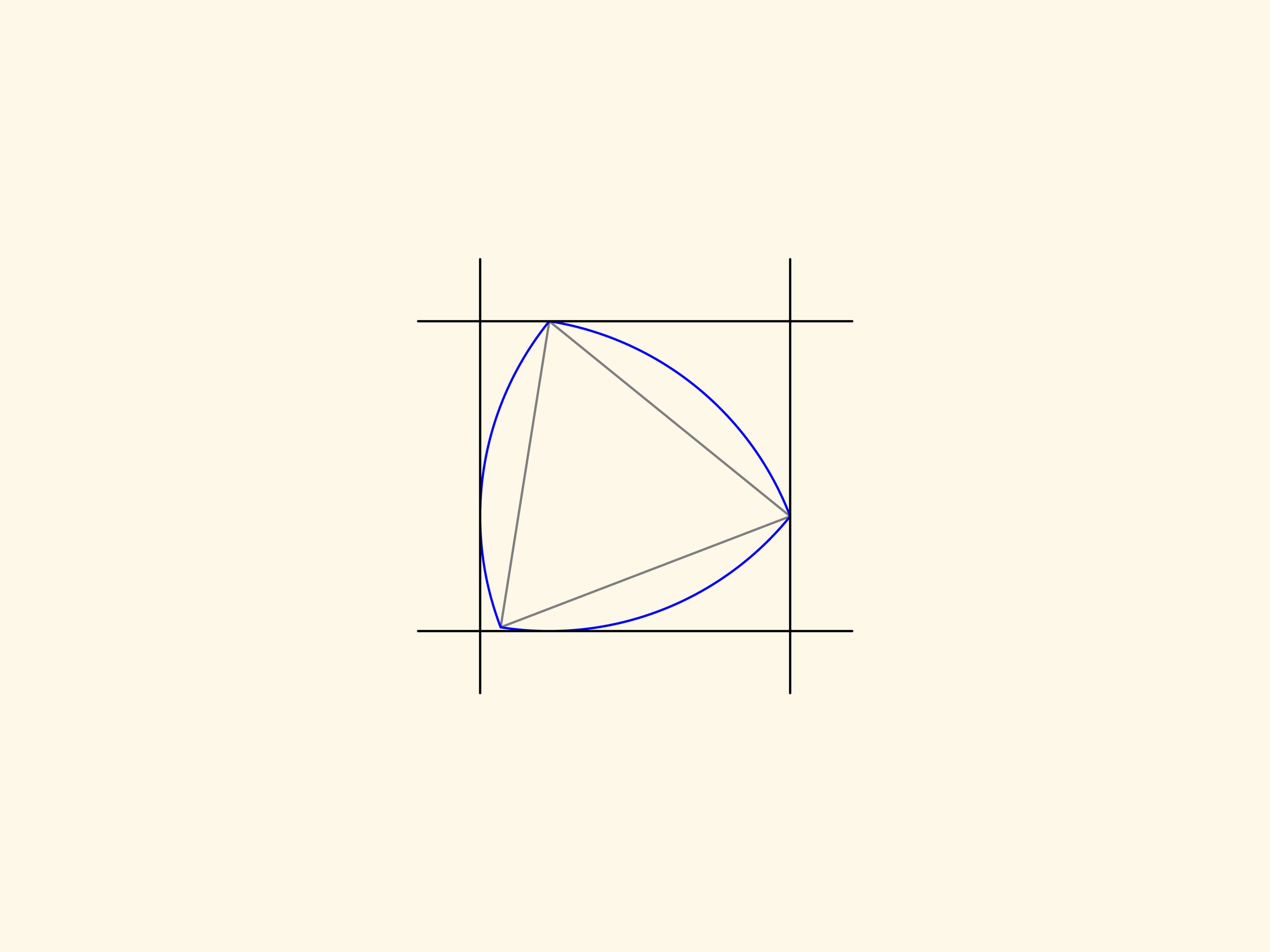
Aggiungiamo un altro paio di linee parallele tangenti al triangolo e che formino un angolo retto con quelle esistenti. Otteniamo così un quadrato. Il triangolo di Reuleaux, se lo si fa ruotare in un modo opportuno, si troverà sempre all’interno del quadrato e in qualsiasi momento sarà a contatto di tutti i lati del quadrato.

Per essere più precisi, dovremmo prendere in considerazione un quadrato con angoli leggermente arrotondati. In questo modo all’interno di questo “quadrato” il triangolo di Reuleaux risulta essere un rotore di area minima, quella figura cioè che, comunque ruotata, toccherà il quadrato in quattro punti, e inoltre essendo la figura minima, quanto ad area, con questa proprietà.

Oltre al cerchio e al triangolo di Reuleaux esistono altre figure ⁠⁠di larghezza costante. Su qualsiasi poligono con un numero dispari di lati, così come sul triangolo, possiamo costruire una curva di larghezza costante. Ci sono anche curve asimmetriche di larghezza costante.

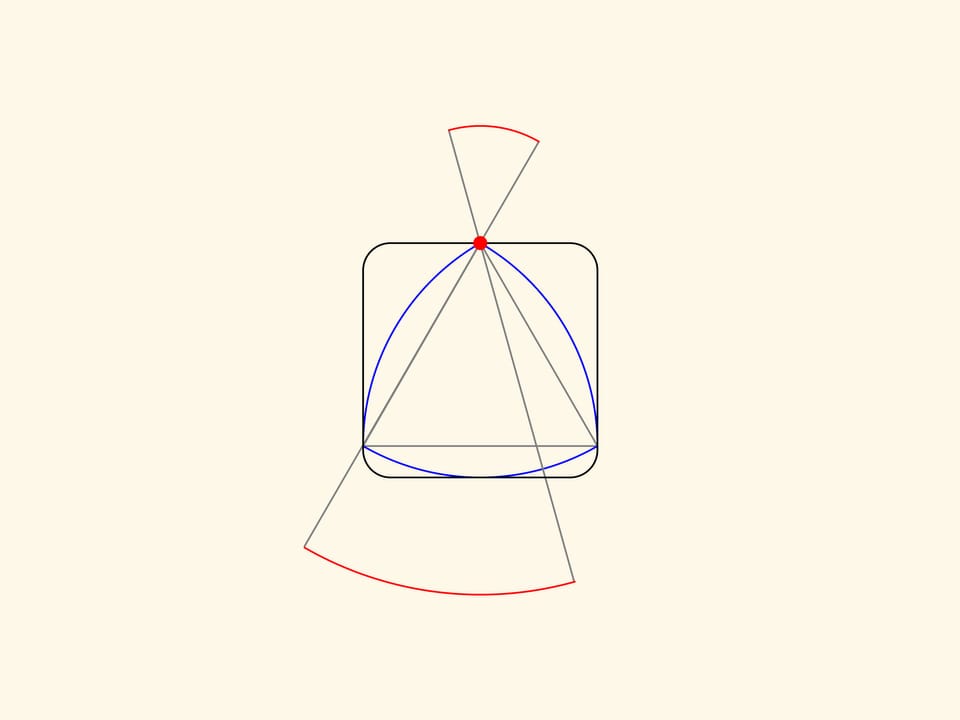
Ma esistono anche infinite altre figure di larghezza costante, costruite esattamente sul triangolo equilatero, e che non sono simili né tra loro, né al triangolo di Reuleaux.

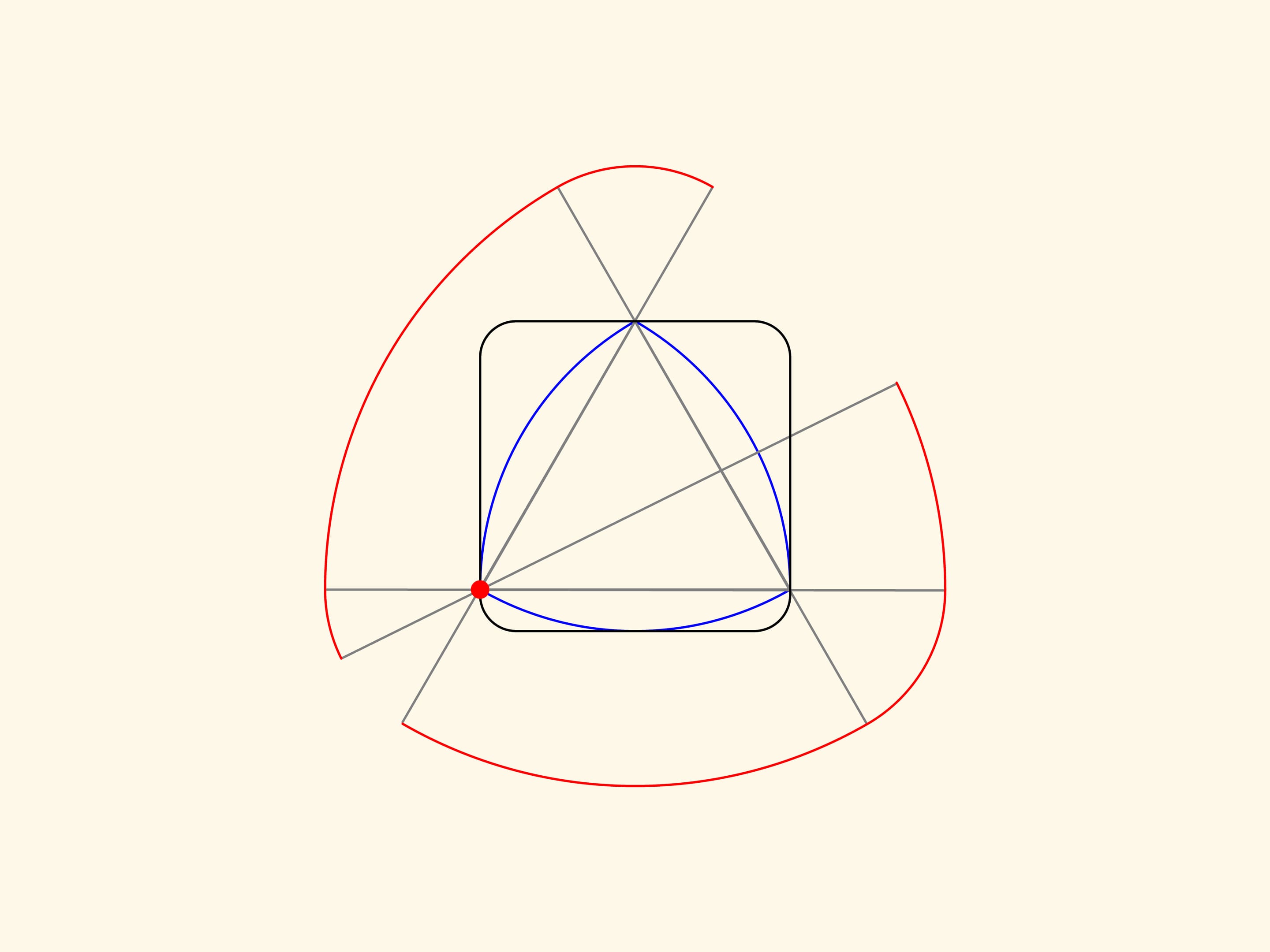
Prolunghiamo uno qualsiasi dei lati del triangolo da entrambi i vertici con segmenti di uguale lunghezza. Facciamo ruotare il lato così prolungato intorno ad uno dei due vertici, fino a che non si sovrappone al lato adiacente. Gli archi, uno più grande e l’altro più piccolo, descritti dalle sue estremità, delimitano la figura di larghezza costante che stiamo costruendo. Ora facciamo ruotare il lato prolungato intorno all’altro vertice, e infine intorno al terzo vertice.

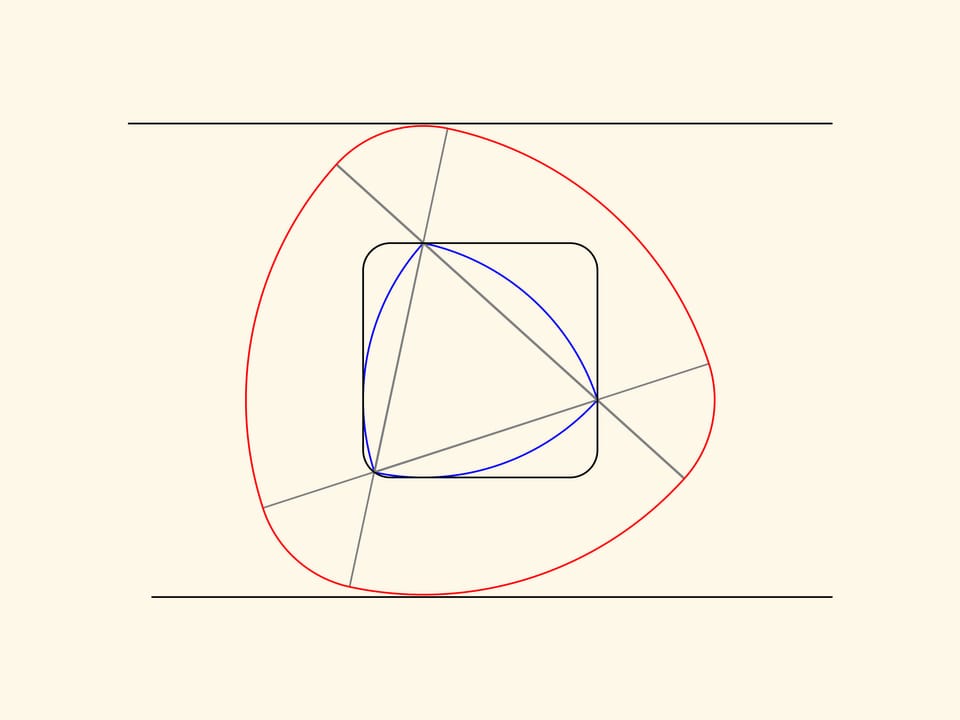
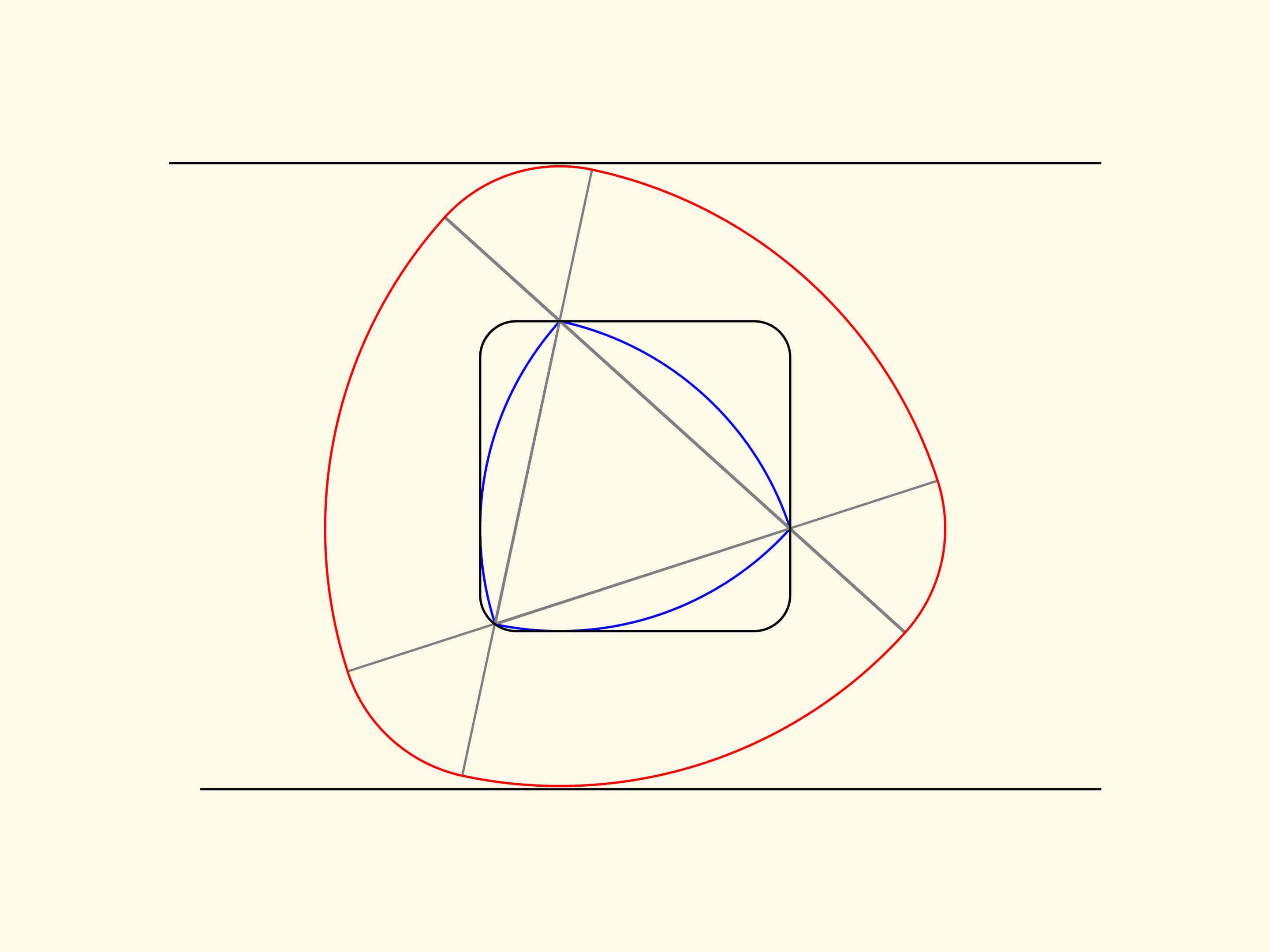
La curva rossa così ottenuta sarà composta di tre archi di raggio maggiore e tre archi di raggio minore. Si può dimostrare che questa curva delimita una figura di larghezza costante. Non importa di quanto vengano allungati i lati oltre i vertici, è importante che siano allungati di segmenti della stessa lunghezza.

Se incominciamo a far ruotare il triangolo di Reuleaux nel quadrato, allora la curva rossa corrispondente ruoterà tra due rette parallele, che non si muovono rispetto al quadrato.

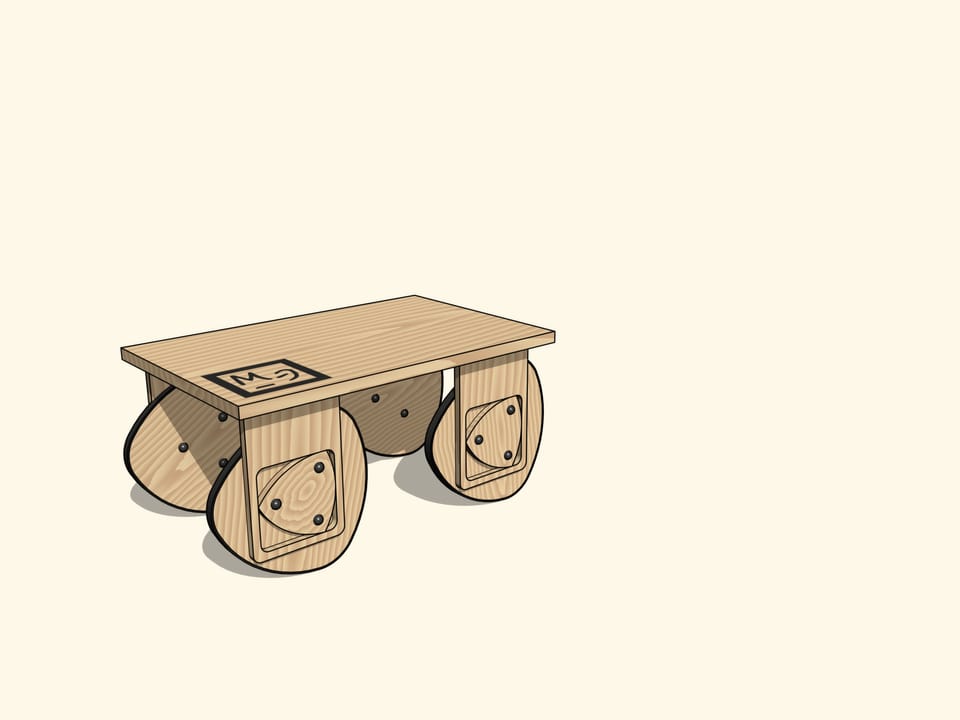
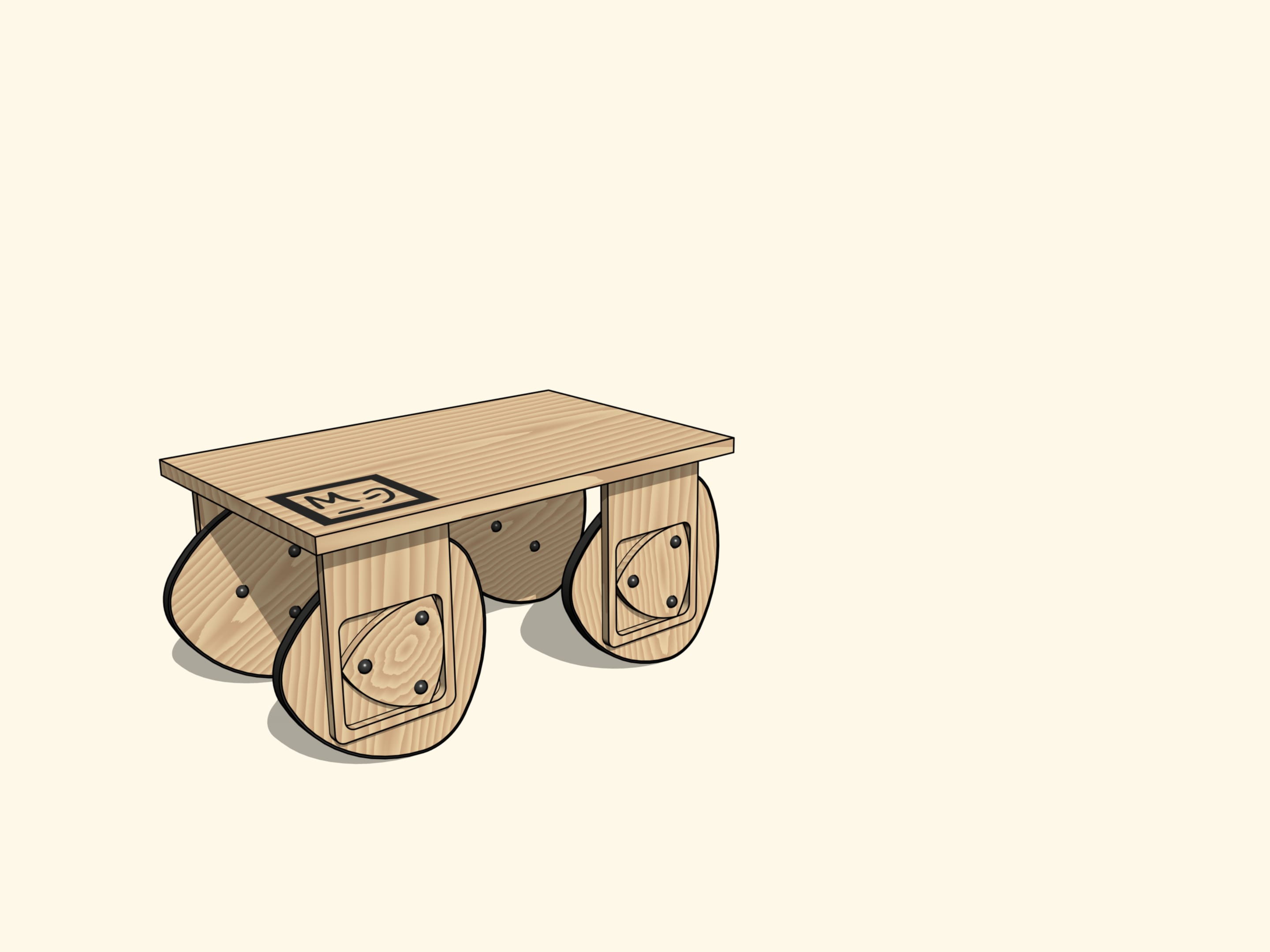
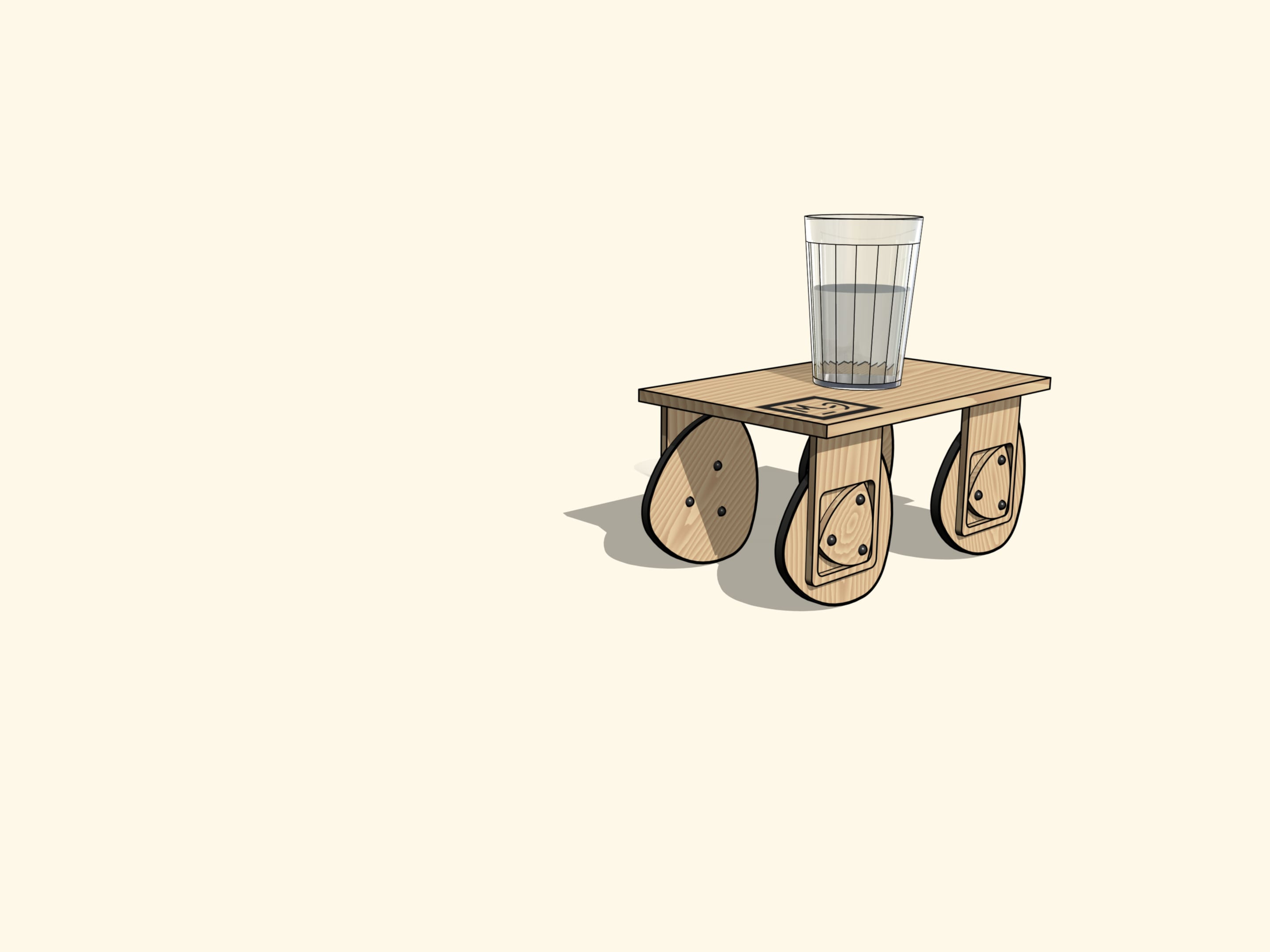
Di conseguenza, si può costruire un carretto con ruote non circolari, col bordo avente la forma della curva rossa.

Poggiato su quattro sospensioni di questo tipo, il nostro carretto si sposterà assolutamente senza sobbalzare!

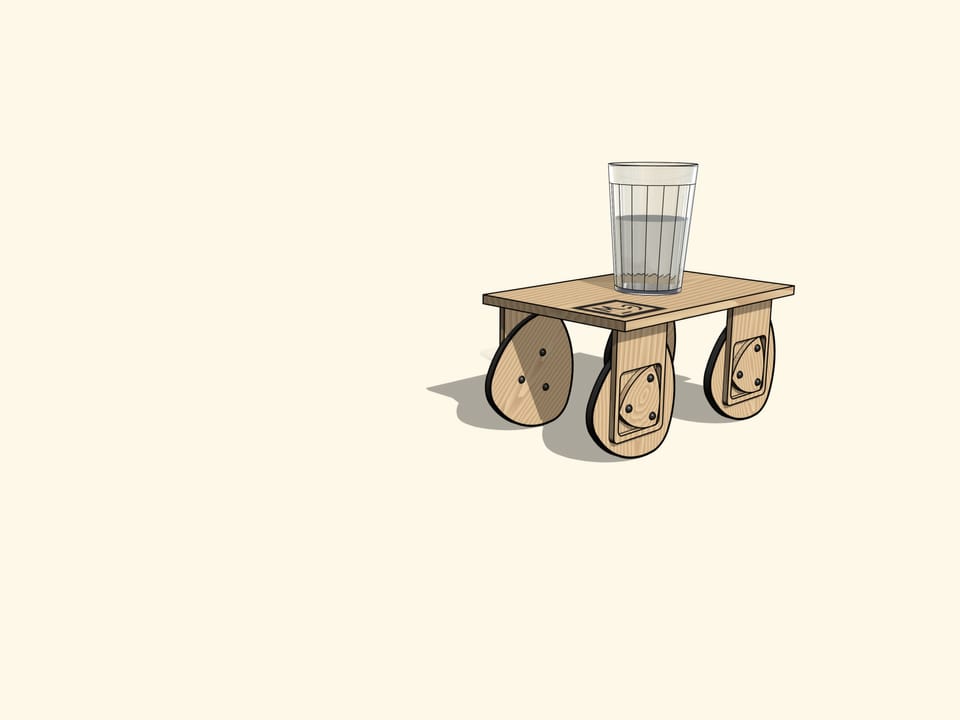
Al fine di garantire che scosse non ce ne sono, mettiamo un bicchiere d’acqua sul nostro carretto, come insegna la tradizione automobilistica. La superficie liscia dell’acqua ci mostra ancora una volta che esistono ruote non circolari con apposite sospensioni fatte in modo che il carro si sposti su di esse assolutamente in orizzontale.