La trisezione dell’angolo ⁠

Il problema della trisezione dell’angolo consiste nel  suddividere un dato angolo in tre parti uguali.

Insieme ad altri due problemi clas­sici di costruzione — la duplicazione del cubo e la quadratura del cerchio — il problema della trisezione dell’angolo è giunto a noi dagli antichi Greci e nel corso di molti secoli occupò le menti dei migliori matematici. Si cercò ripetutamente di risolvere questi problemi facendo uso degli strumenti sacri della geometria euclidea: la riga e il compasso. Tra l’altro, già nell’anti­chità i matematici avevano intuito che, usando solo riga e compasso, questi problemi erano irresolubili, ma più tardi ciò fu anche      dimostrato. I tentativi di allargare l’insieme degli strumenti permessi ebbero una grande influenza sulla matematica dell’antica Grecia, e condus­sero ai primi studi delle sezioni coniche, alla ricerca di curve complicate, e alla costruzione di strumenti interes­santi.

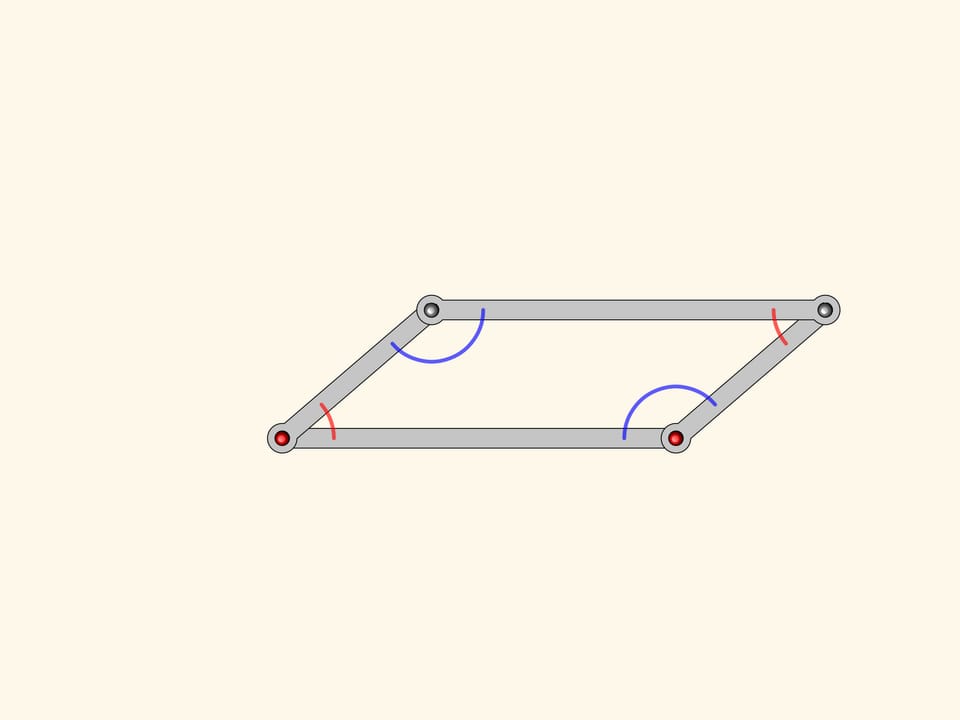
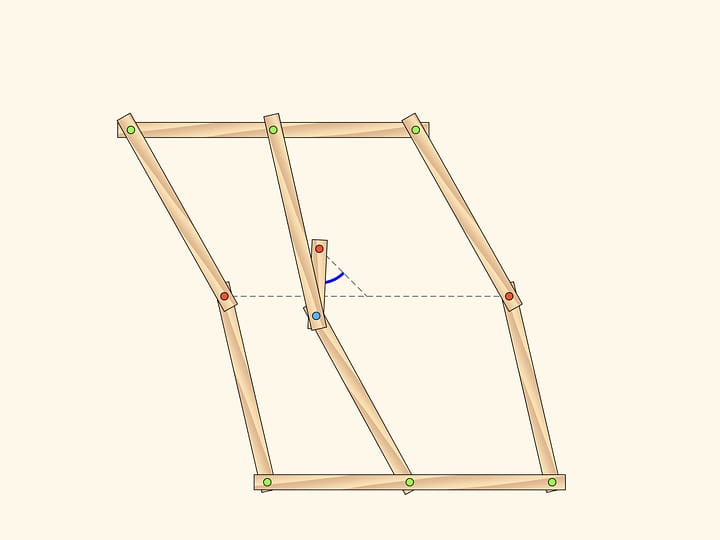
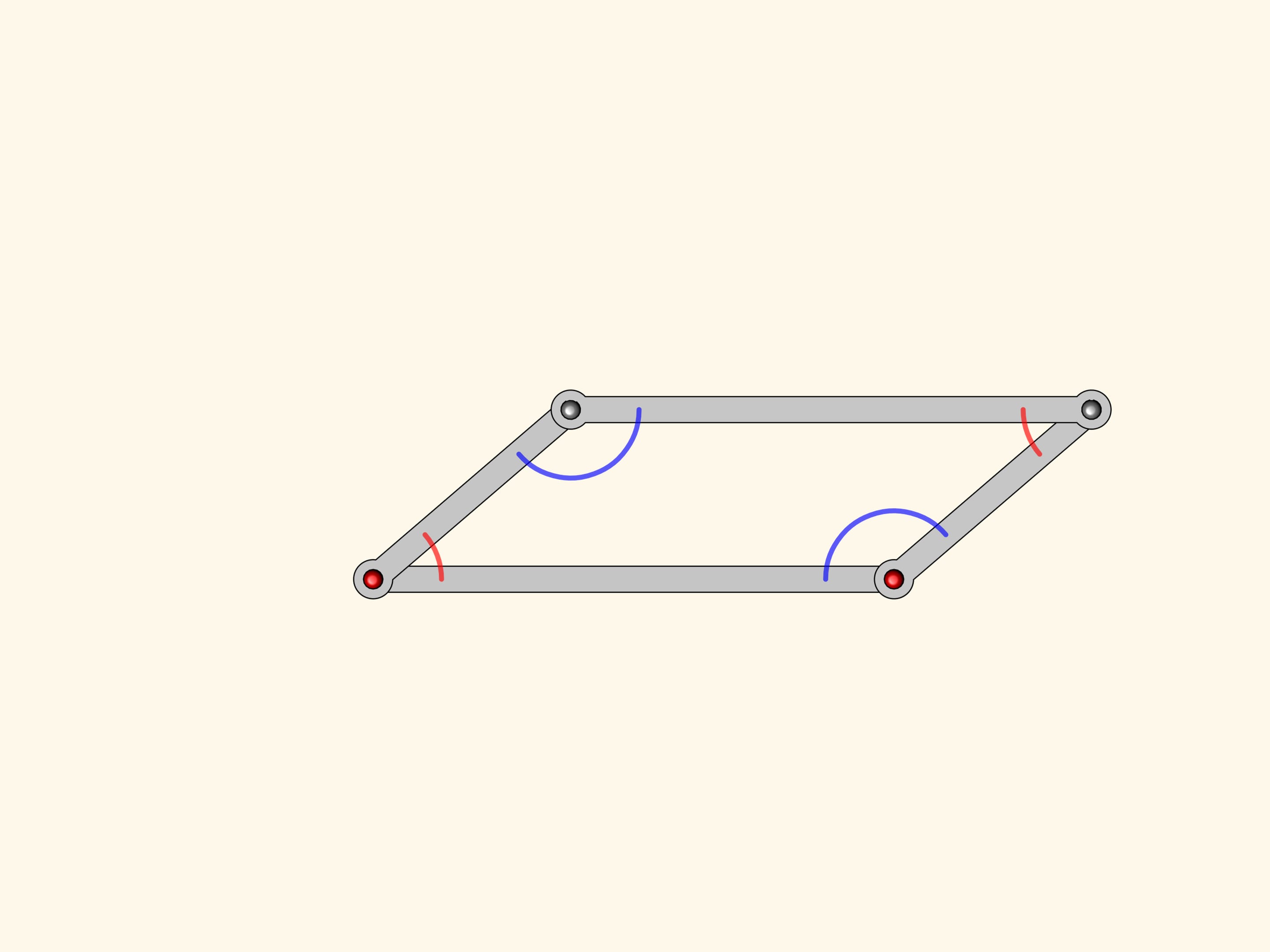
Consideriamo un meccanismo a cerniere, costituito da un parallelogramma con due cerniere fisse. Dal corso di matematica a scuola vi ricorderete  che gli angoli opposti di un parallelogramma sono uguali. Questo è vero per un parallelogramma qualsiasi, e quindi anche per il nostro meccanismo, in qualsiasi modo venga inclinato.

Proprio in qualsiasi modo venga inclinato?

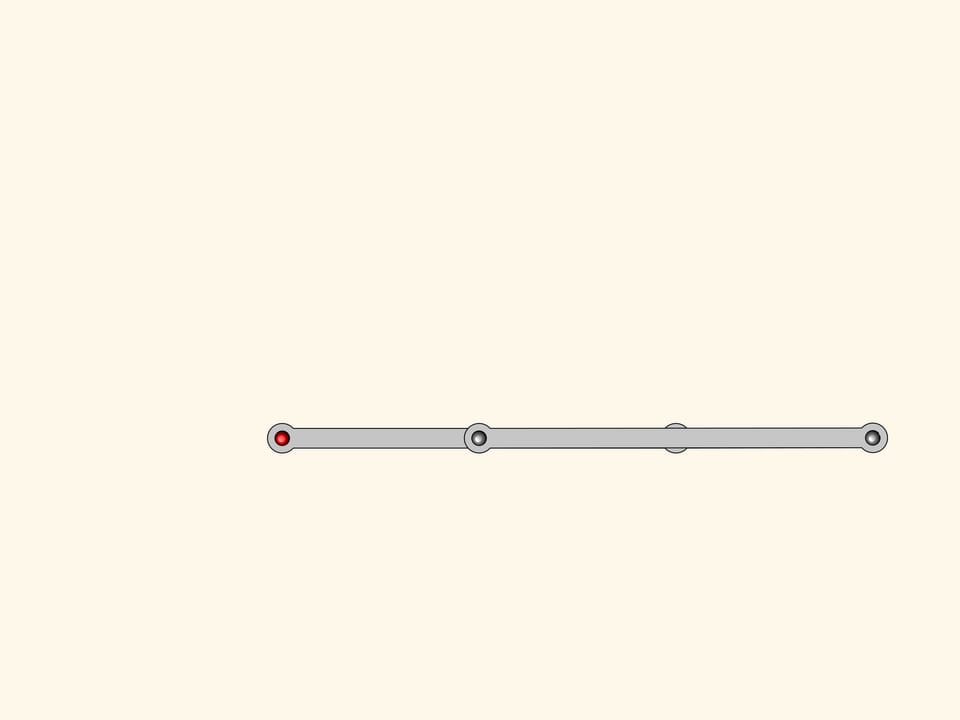
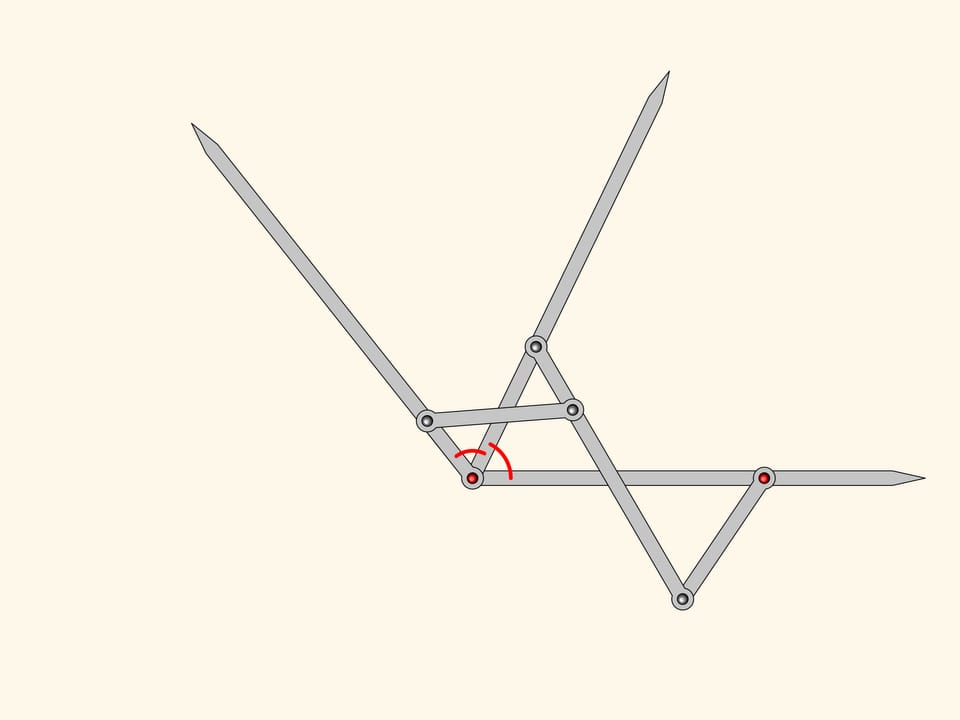
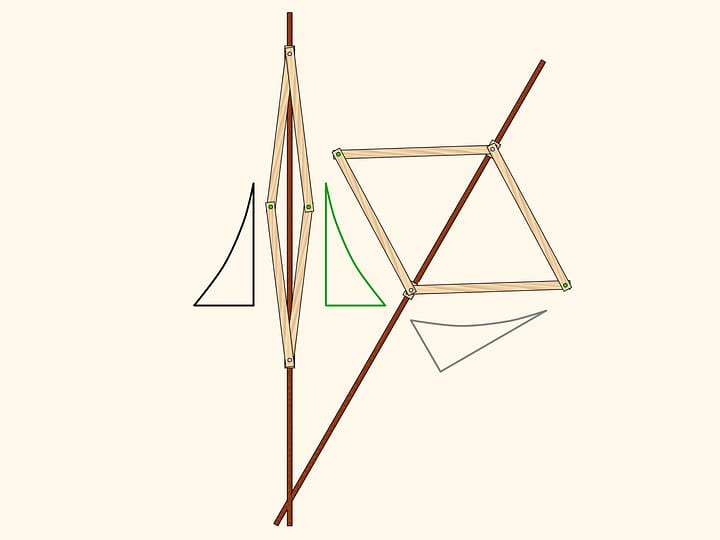
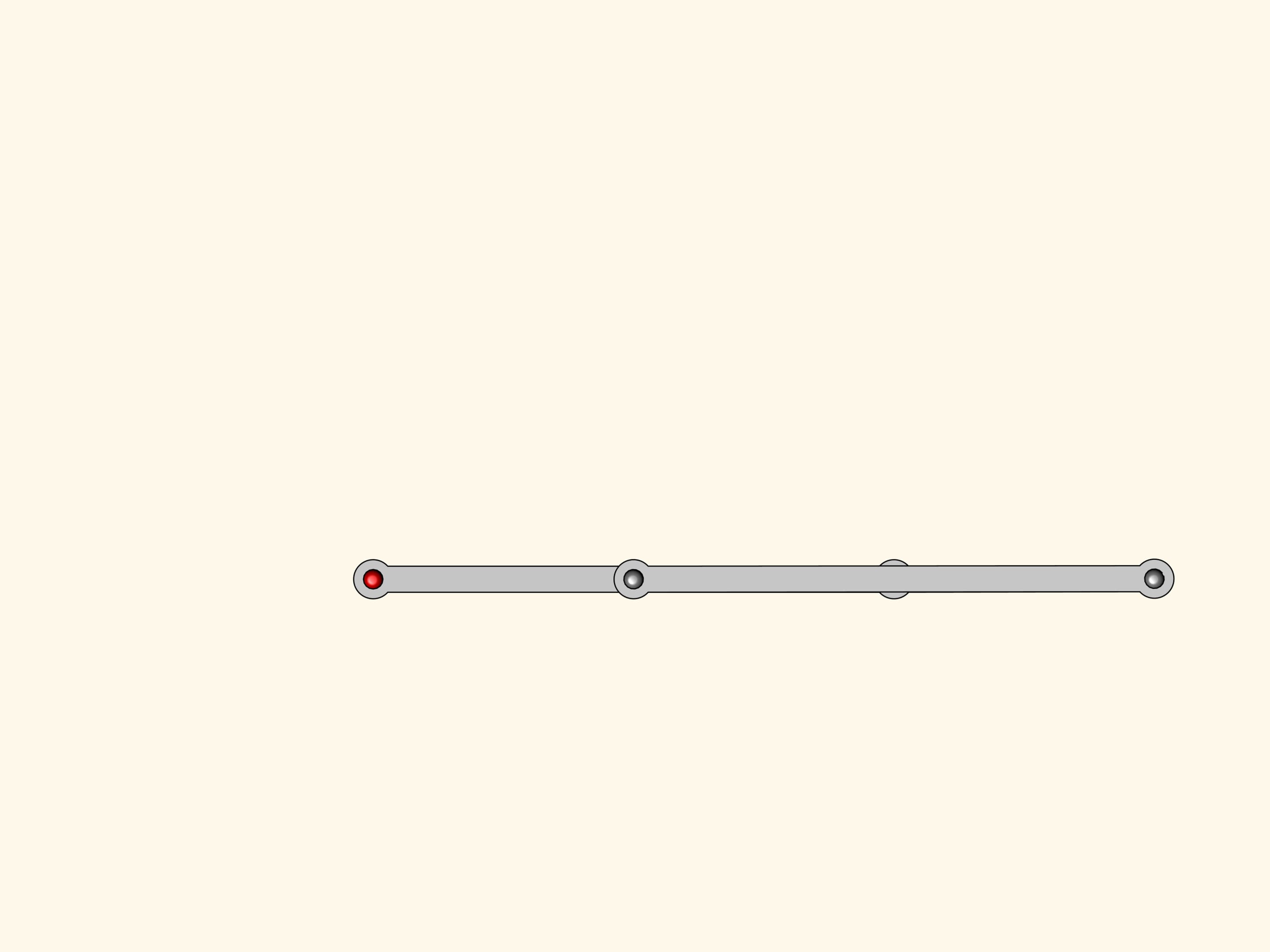
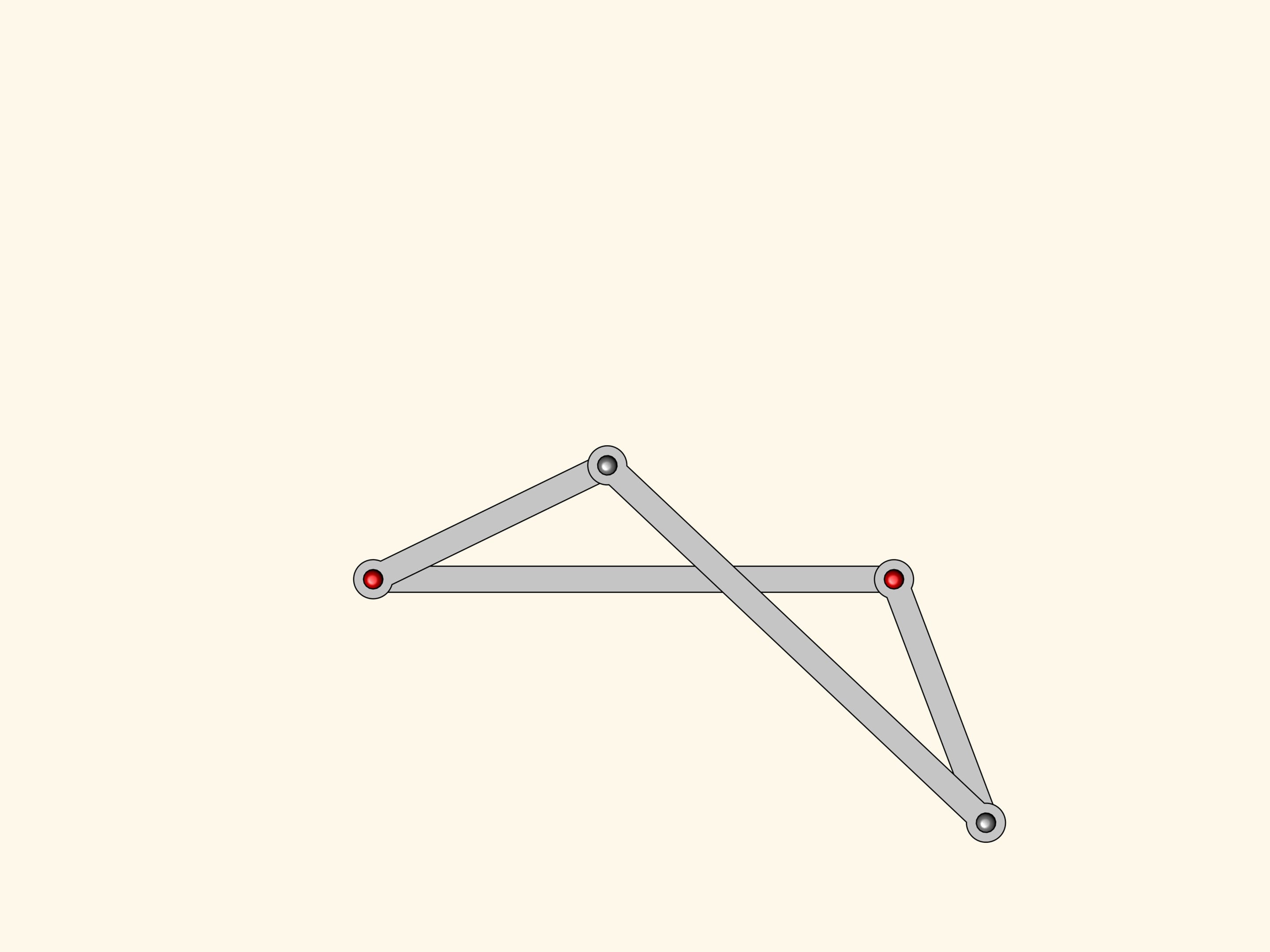
Il nostro sistema ha una punto singolare,  quando tutte le barre giacciono sulla stessa retta. Da questo punto di biforcazione il meccanismo può venir fuori sia diventando di nuovo un parallelogramma, sia trasformandosi in una figura che si chiama anti­parallelogramma.

Proprio questa singolarità del meccanismo a cerniere che abbiamo considerato era la causa di un errore nei ragionamenti di Alfred Kempe, il quale nel 1876 “dimostrò” il teorema, che esiste un meccanismo a cerniere, capace di falsificare la vostra firma e non può disegnare e nient’altro all’infuori di essa. Più precisamente, che qualsiasi curva algebrica che si trovi in una regione limitata di piano è la traiettoria di qualche meccanismo planare a cerniere. Il teorema stesso è vero, ma  nel 1984 trovarono che c’era un errore nella dimostrazione di Kempe, errore che fu corretto  solo alla fine del XX secolo.

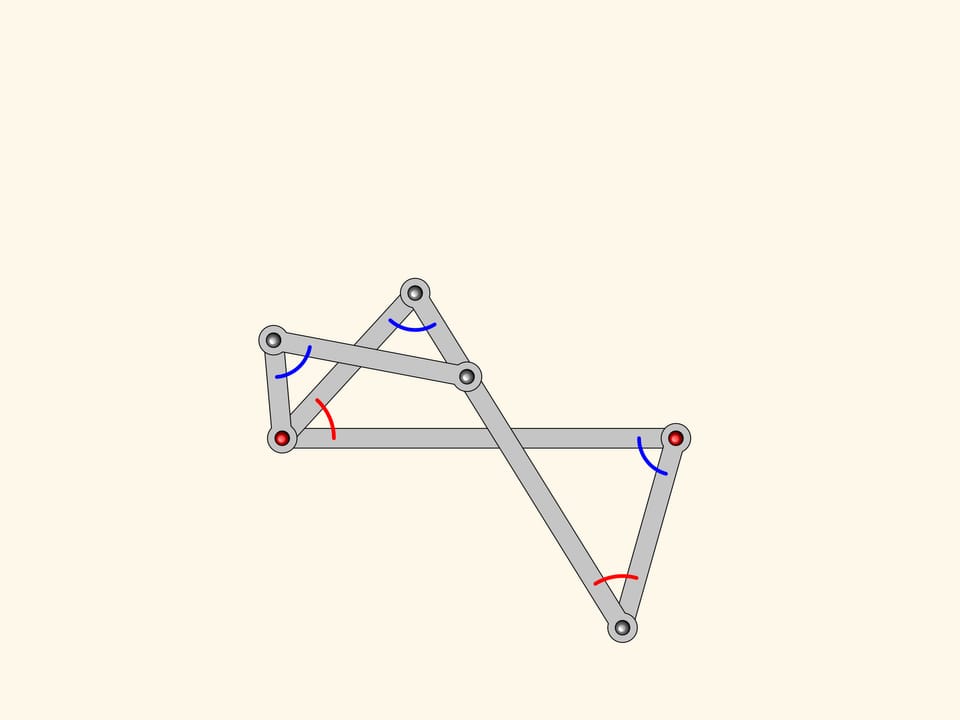
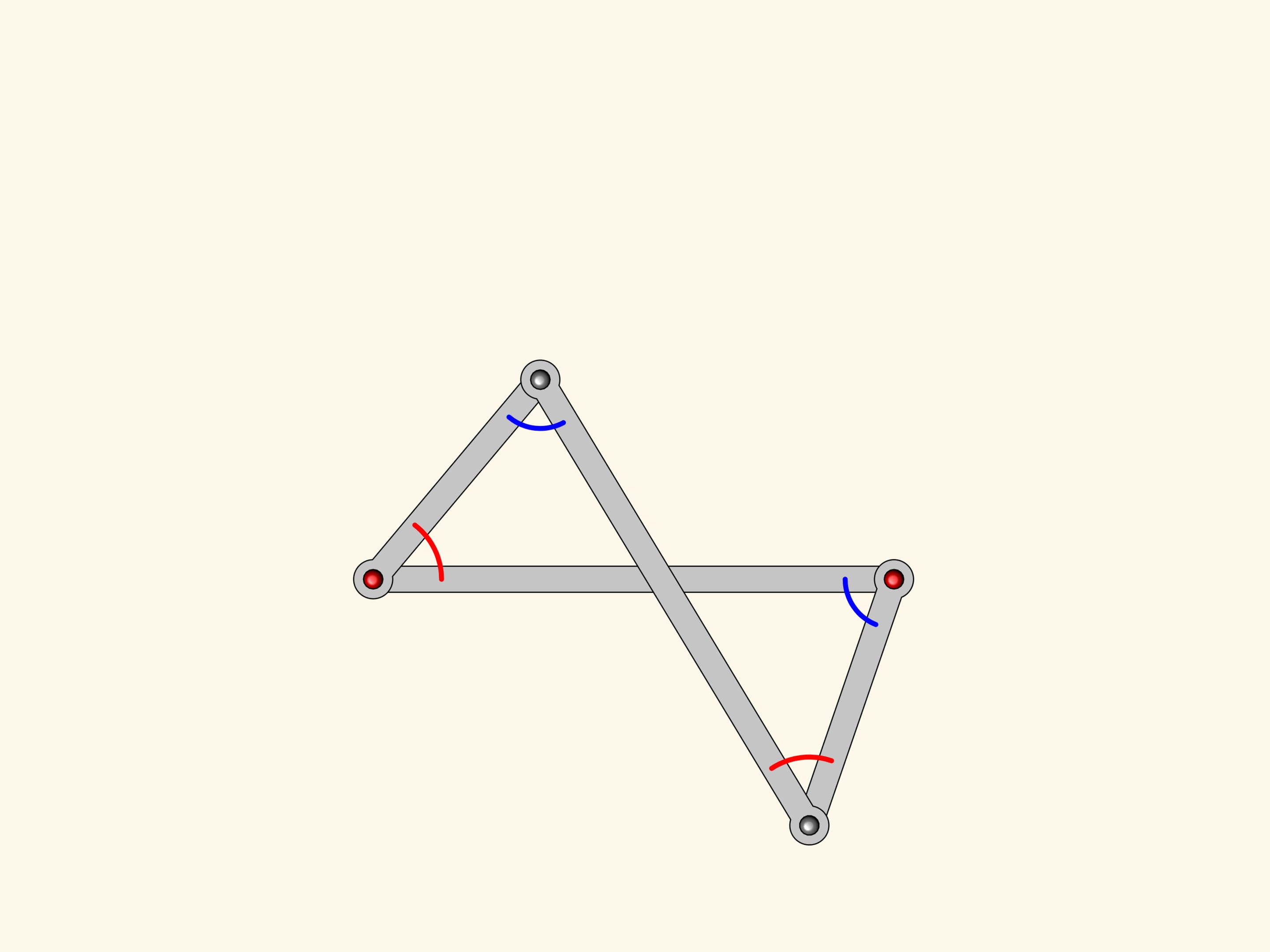
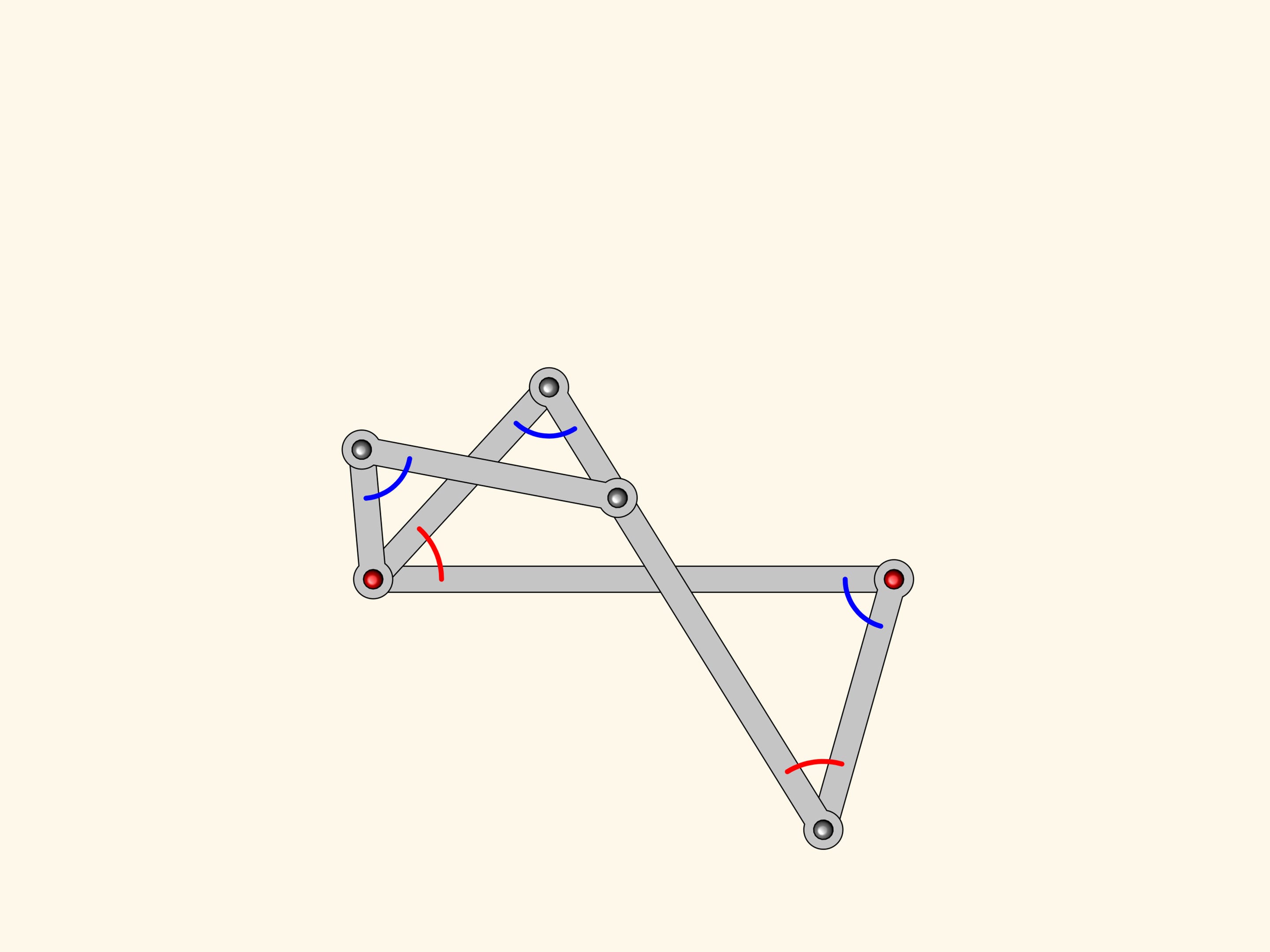
Dal parallelogramma l’anti­parallelogramma eredita la proprietà che due lati opposti sono uguali; gli altri due, che si intersecano tra loro, anche sono uguali. Ma la nostra figura possiede pure una relazione tra gli angoli: anche nell’anti­parallelogramma sono uguali a due a due!         

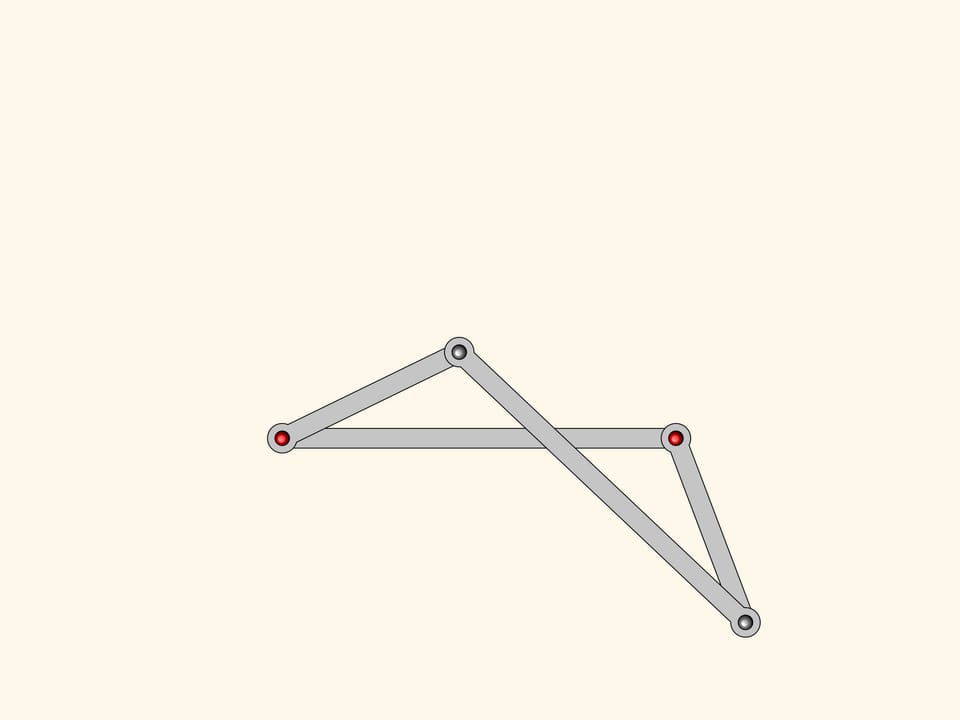
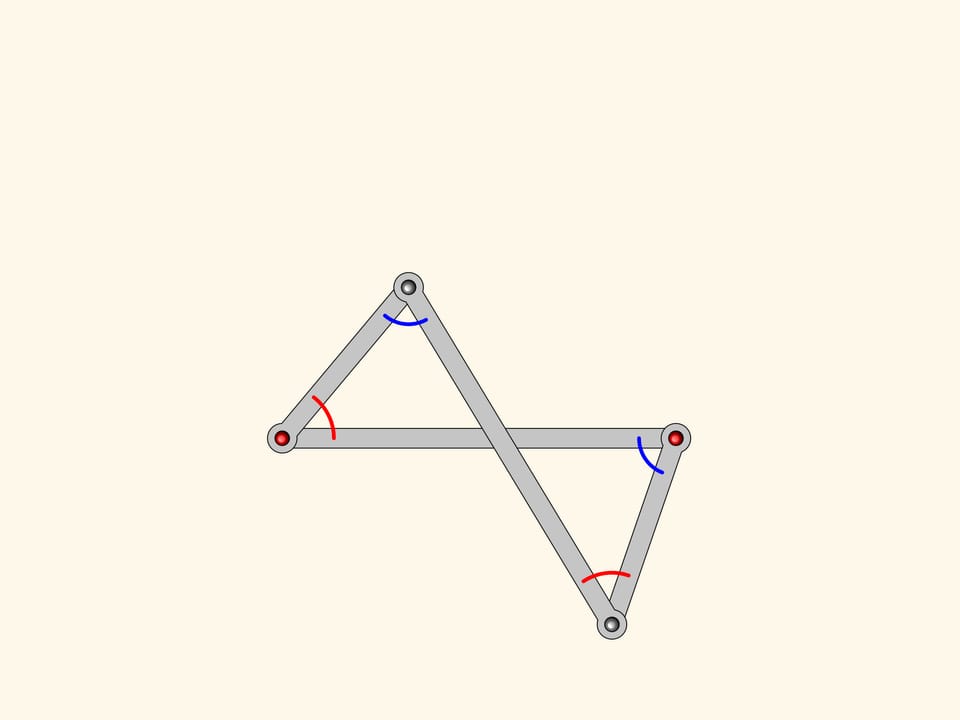
Aggiungiamo al nostro anti­parallelogramma un altro anti­parallelogramma più piccolo, ma simile al primo. Essi hanno un angolo in comune, il che significa che gli angoli  segnati in rosso sono uguali.

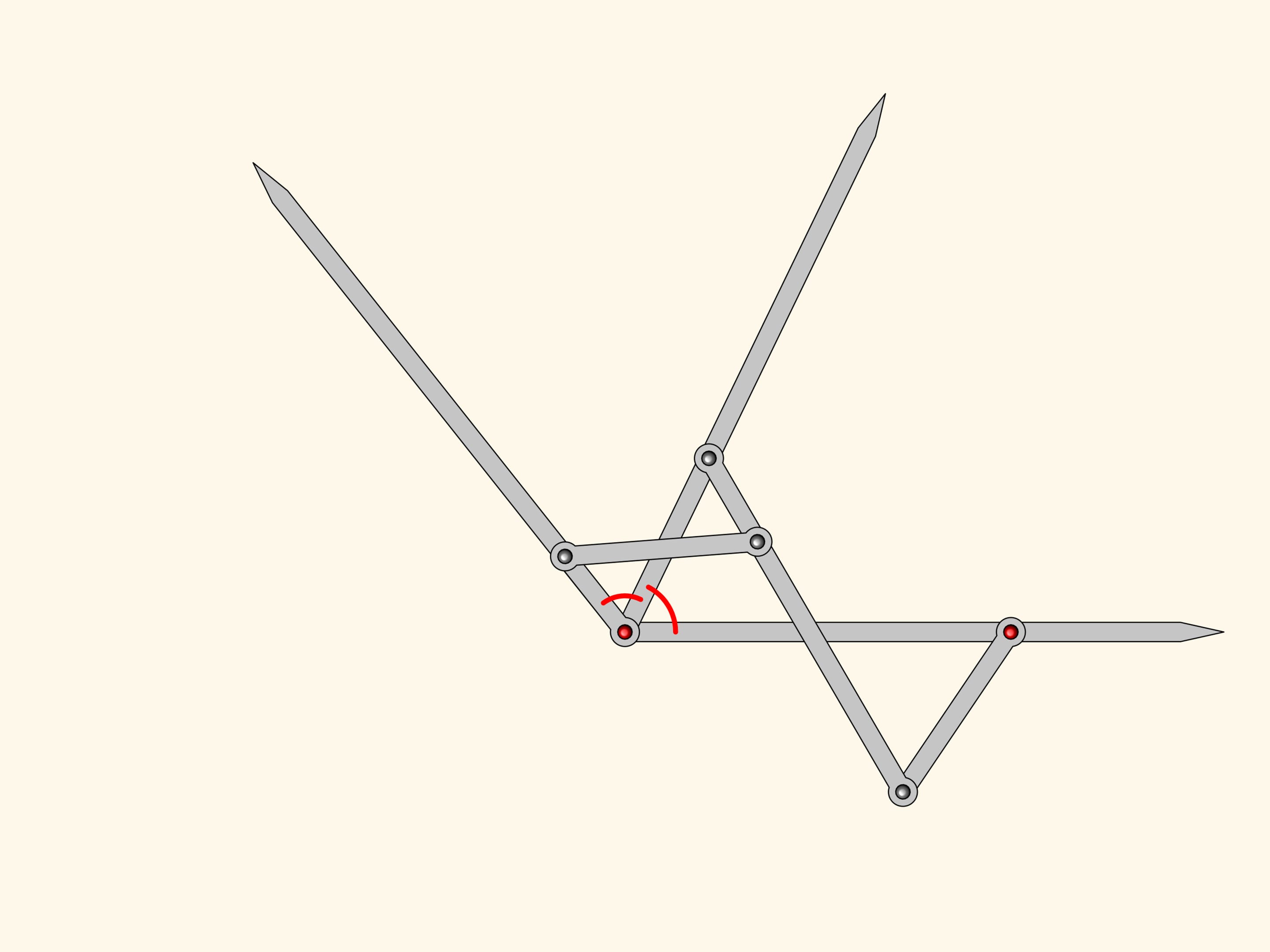
Prolungando i lati di questi angoli, otteniamo un meccanismo planare a cerniere che può essere utilizzato per costruire la bisettrice di qualsiasi angolo.

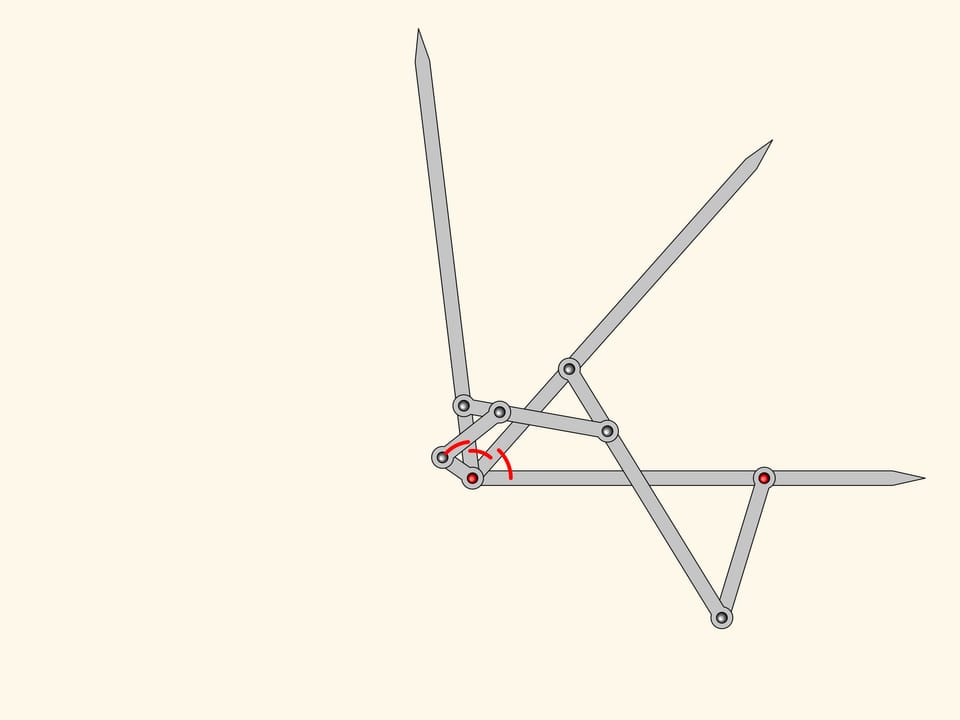
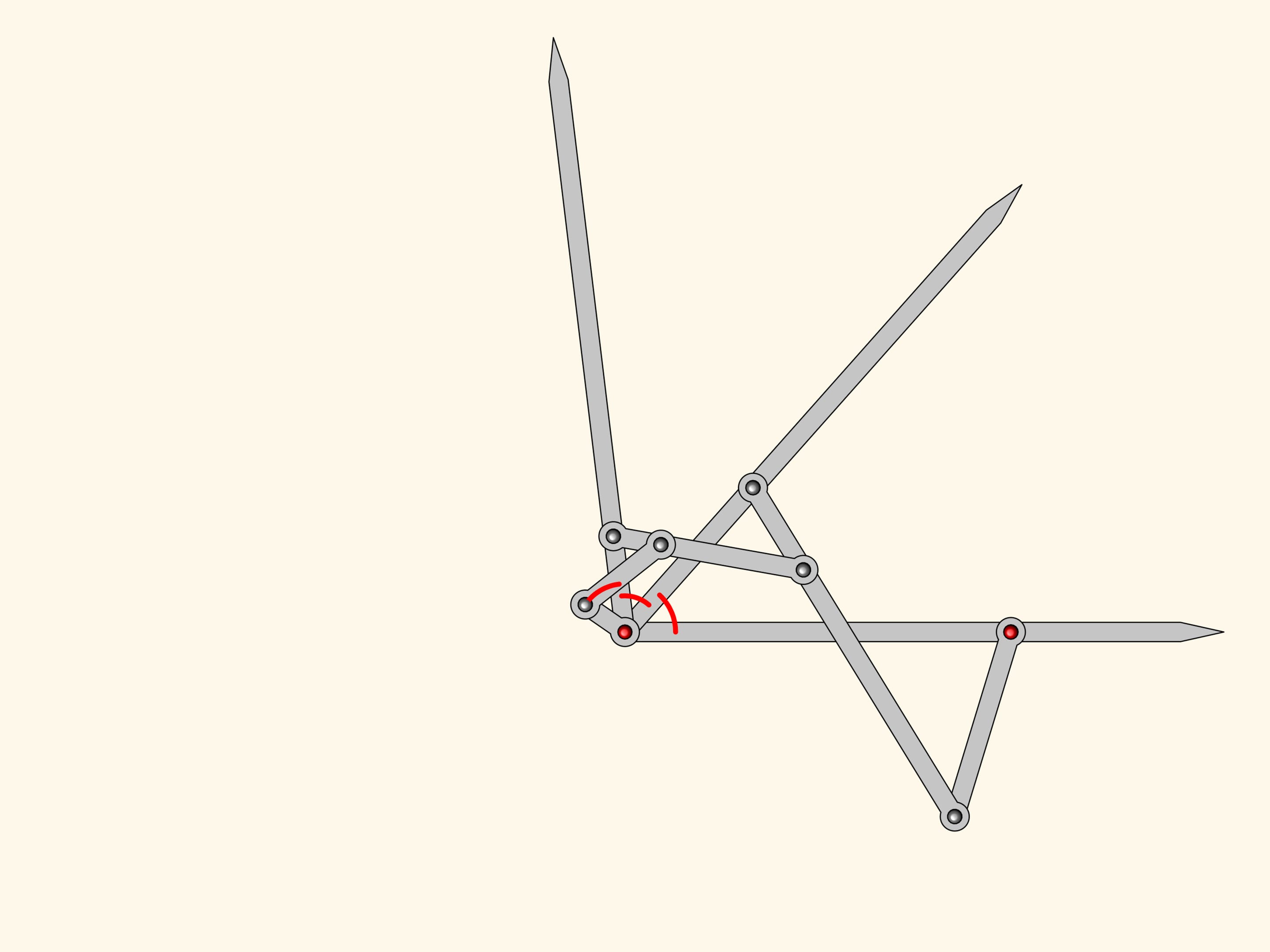
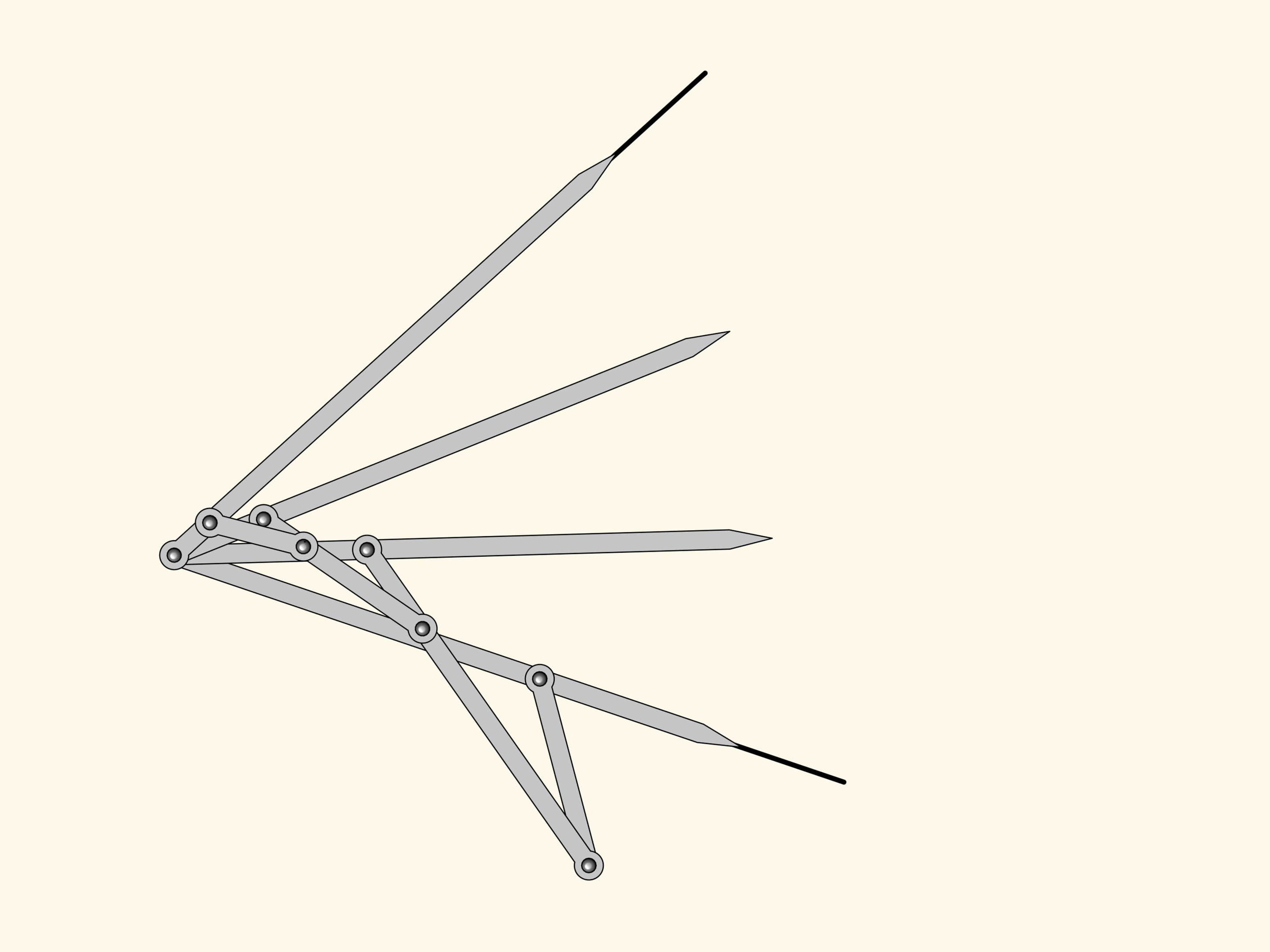
Possiamo ora aggiungere ancora un altro anti­parallelogramma simile ai primi due. Con lo stesso ragionamento il suo angolo vicino alla cerniera in rosso sarà uguale agli altri due adiacenti, che già abbiamo dimostrato essere uguali.

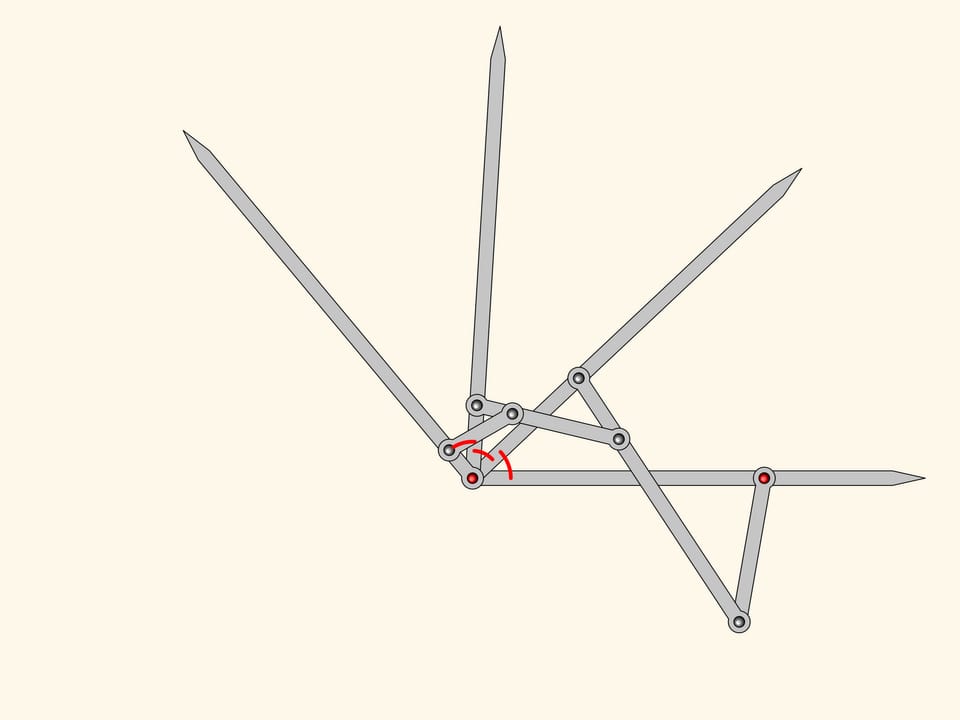
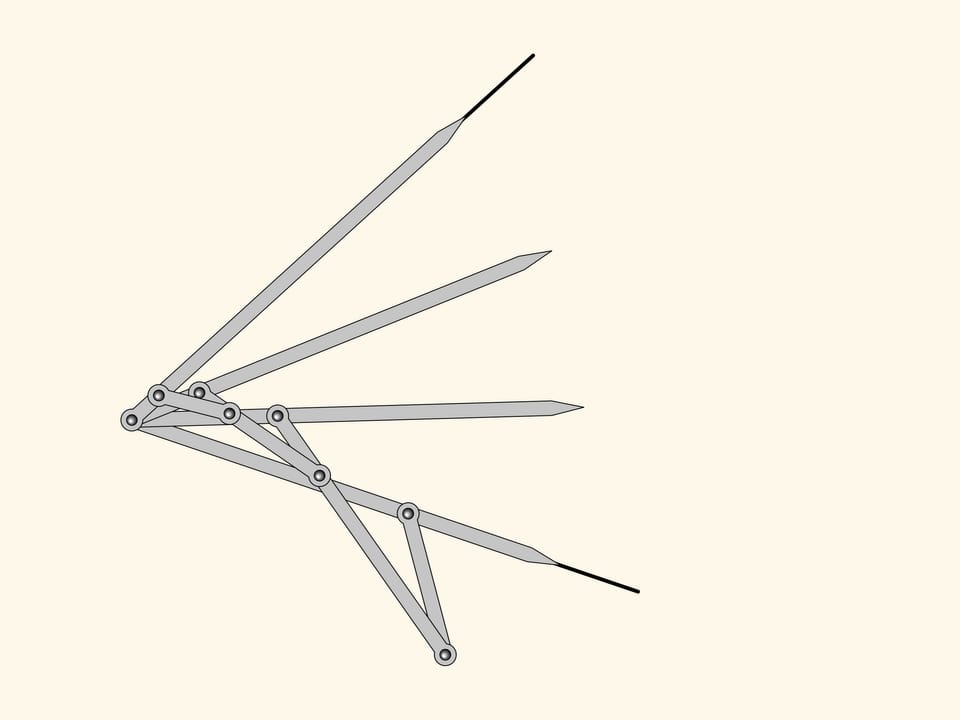
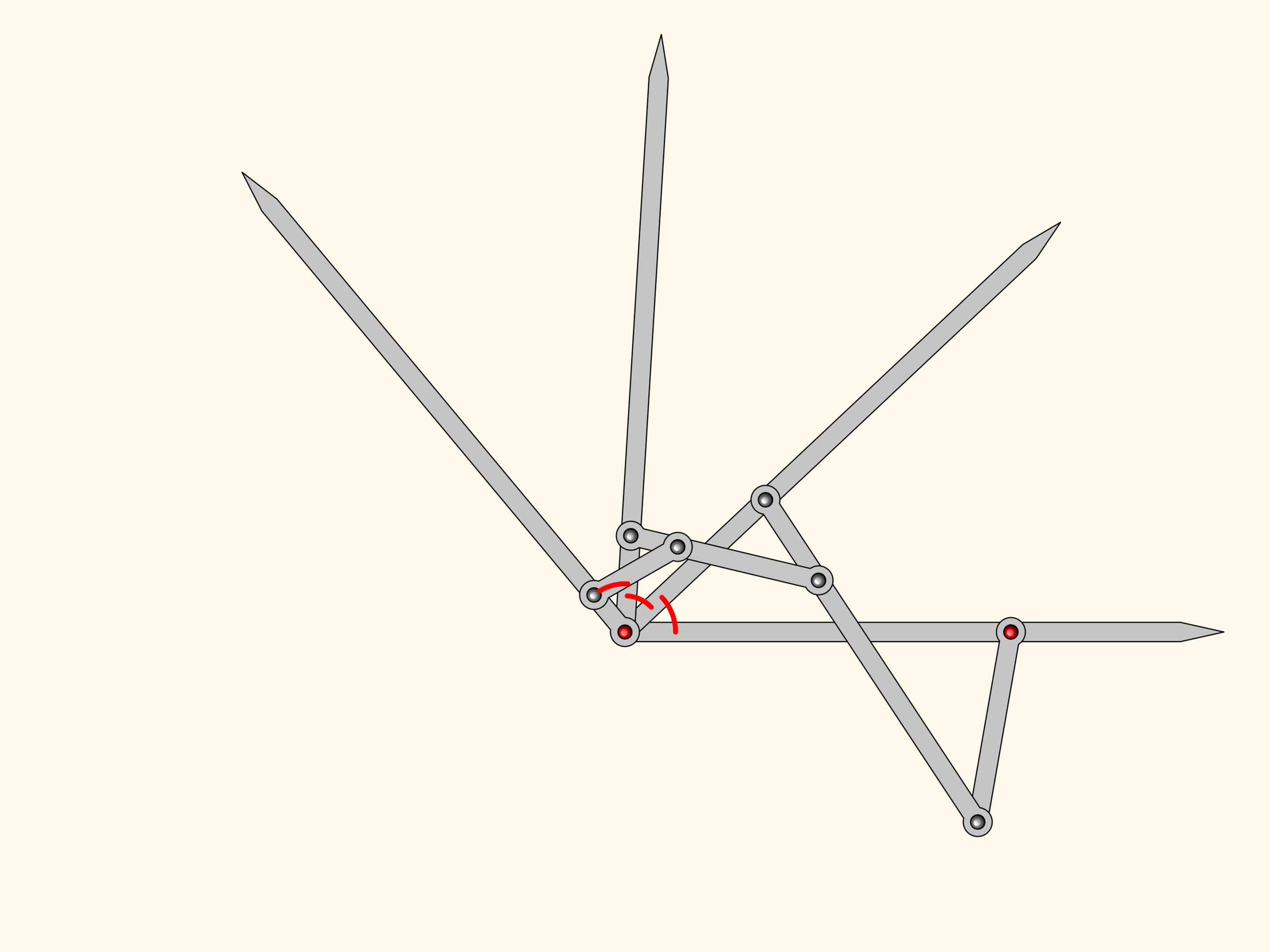
Il meccanismo planare a cerniere che abbiamo ottenuto è un trisettore di angoli, e quindi risolve il problema di dividere un angolo qualsiasi in tre parti uguali!

Kempe non andò oltre a questo meccanismo, poiché nella sua “dimostrazione” del teorema della “firma” era neces­sario un meccanismo che dividesse un angolo esattamente in tre parti. Tuttavia è evidente che si può continuare ulteriormente l’algoritmo di costruzione del trisettore, ottenendo dei meccanismi a cerniere che dividono un angolo qualsiasi in un numero arbitrariamente fissato di parti uguali