Su un foglio di carta è disegnato un poligono arbitrario. È possibile piegare il foglio di carta in modo che sia possibile ritagliare il poligono facendo un solo taglio rettilineo?
Consideriamo il caso più semplice, cioè un triangolo arbitrario.
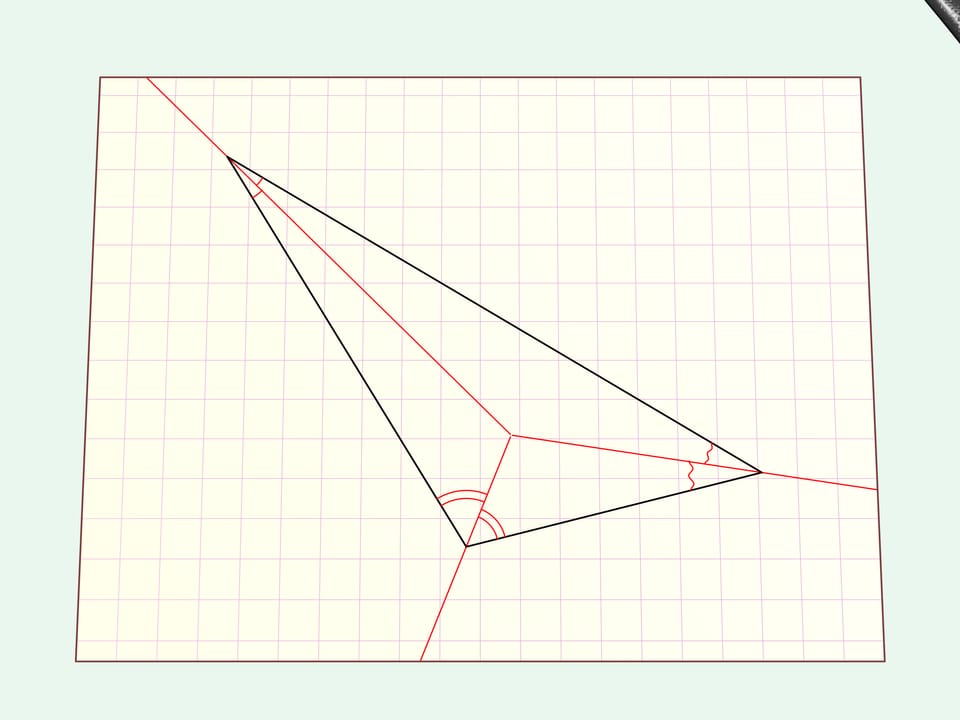
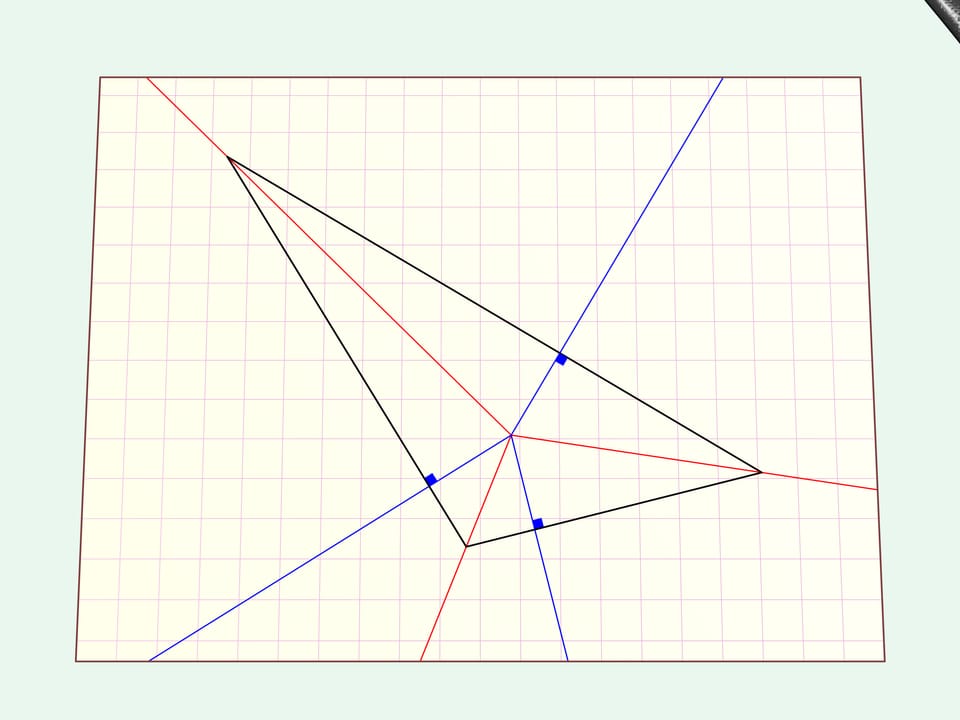
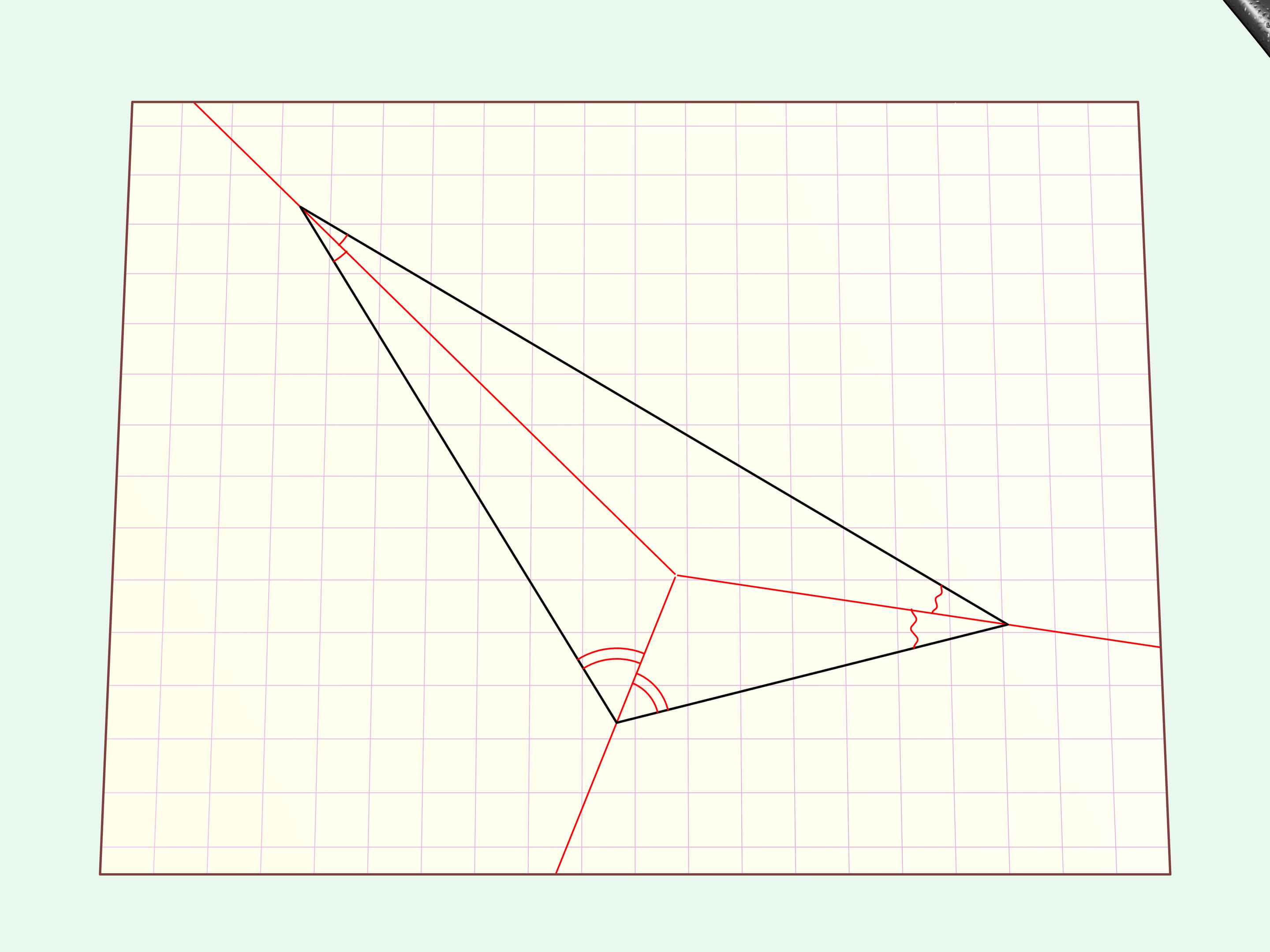
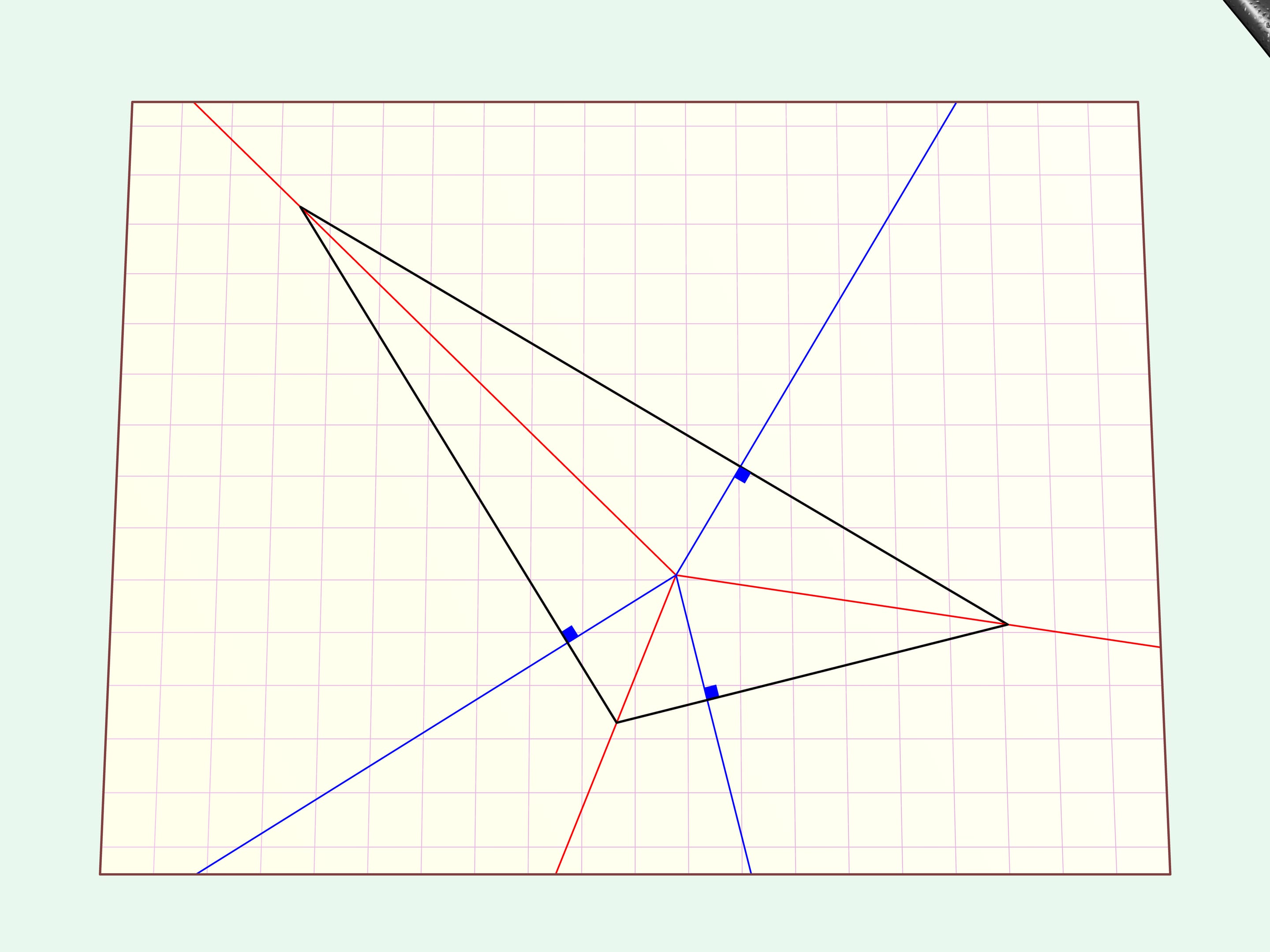
Tracciamo le bisettrici e dal punto del loro incontro tracciamo le perpendicolari ai lati del triangolo.
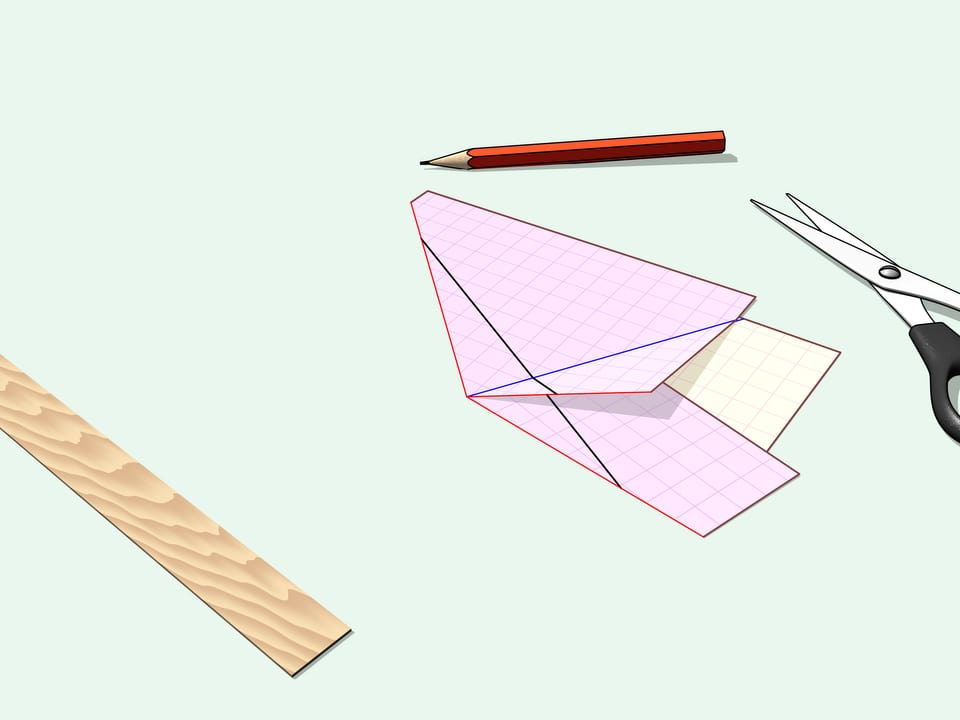
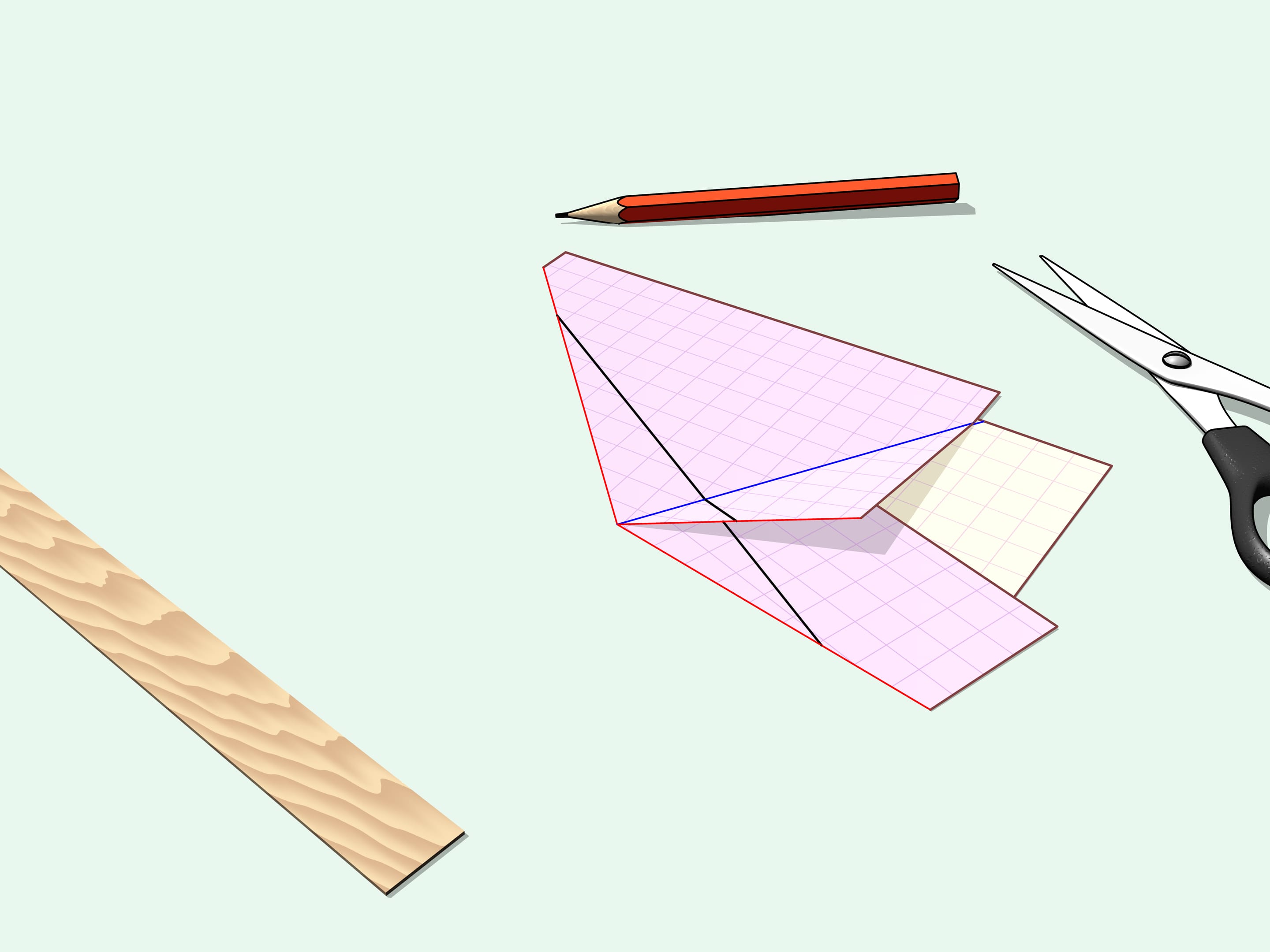
Piegheremo il foglio di carta lungo tutti questi raggi. Tutto il bordo del triangolo — ossia i suoi lati — giaceranno sulla stessa retta. Facciamo un taglio dritto lungo di essa.
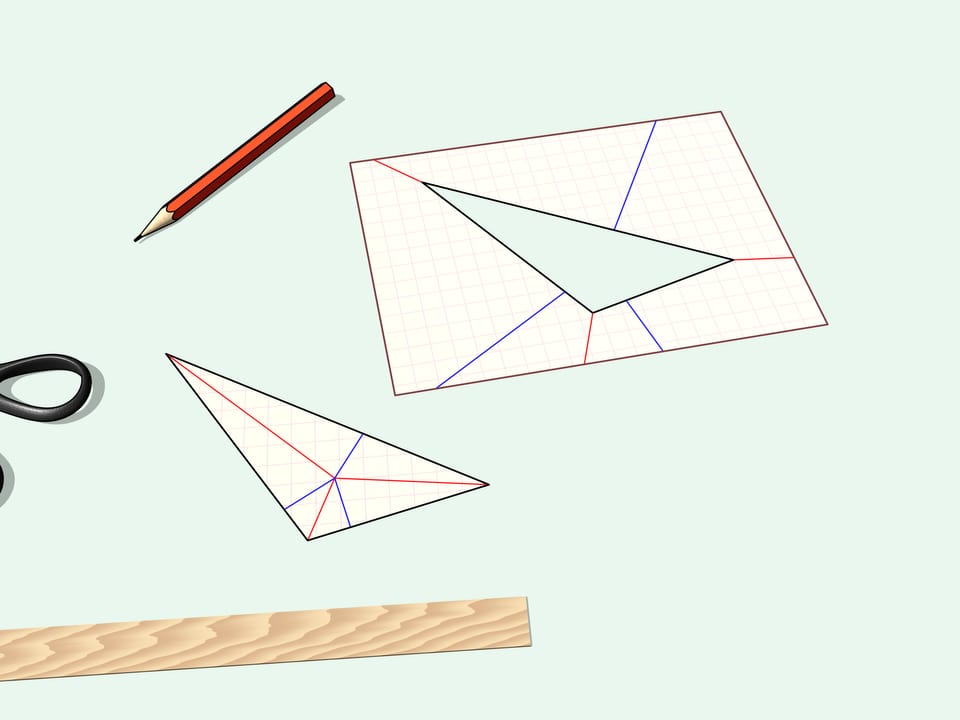
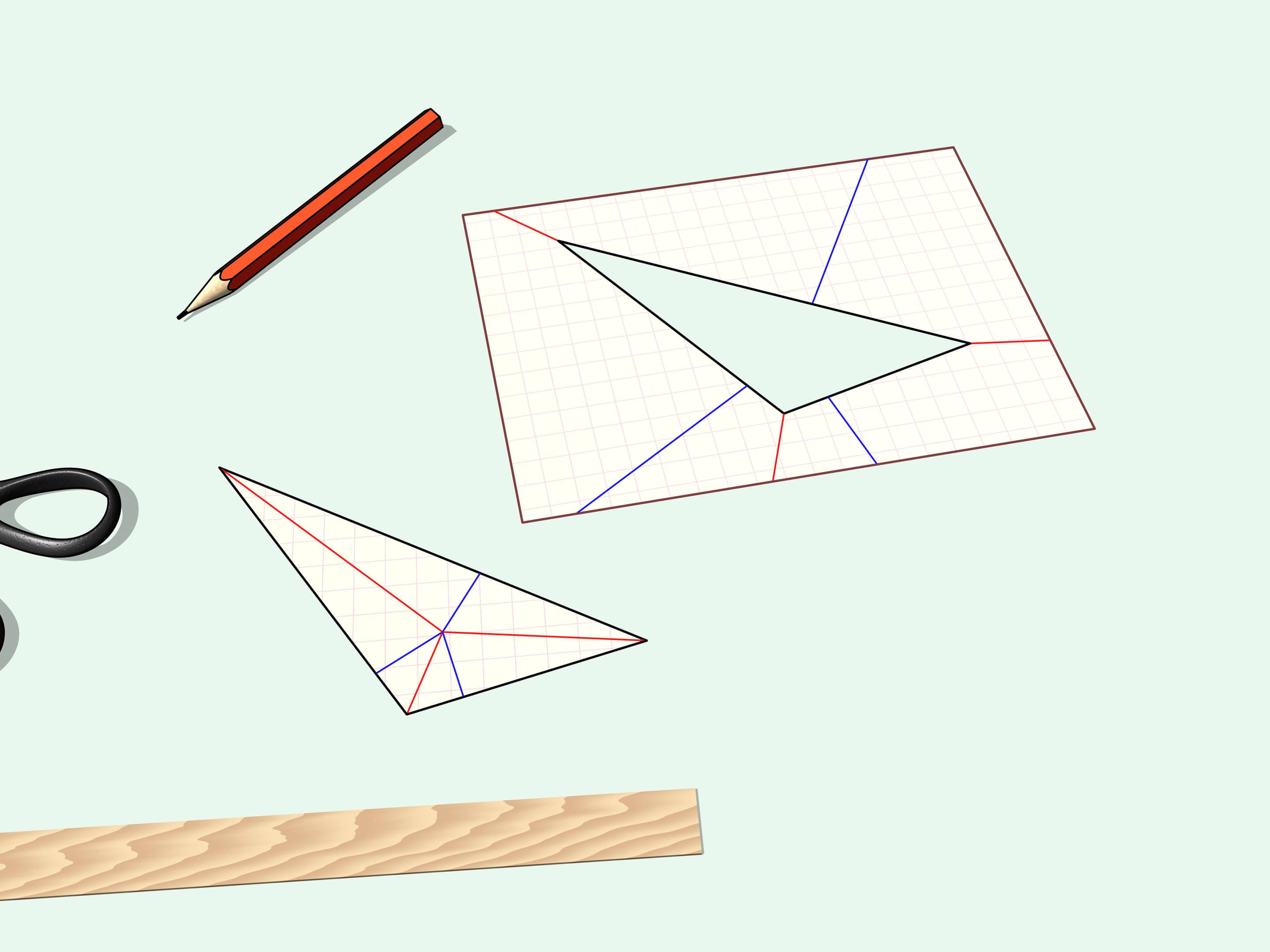
Dispieghiamo l’angolo ritagliato: ecco il nostro triangolo iniziale. Se dispieghiamo anche il restante pezzo di carta, vediamo che non è stato ritagliato niente di più del nostro triangolo, infatti anche il buco ha la forma del nostro triangolo iniziale.
Disegniamo ora una stella a cinque punte. Si tratta di un poligono non convesso con dieci vertici. In questo caso però la soluzione del problema è facilitata dalla simmetria della stella. Tracciamo i raggi che dal centro vanno verso i vertici della stella, e pieghiamo il foglio di carta lungo di essi. Ritagliamo l’angolo ottenuto e dispieghiamolo: ecco la nostra stella. Dispiegando quello che resta del foglio vedremo un buco a forma di stella.
Ma anche il poligono complicato, disegnato all’inizio del film, può essere ritagliato con un unico taglio dritto! Infatti, nel 1998 fu dimostrato il seguente teorema generale.
Altri etudi in “Geometria della carta”
