Uscire nello spazio⁠

Vivendo sulla superficie della Terra, gli uomini credettero per lungo tempo che essa fosse piatta. Fu neces­saria la costruzione di teorie scientifiche per capire che la Terra è simile a una sfera. E soltanto nella seconda metà del XX secolo gli uomini poterono constatarlo coi propri occhi, quando guardarono la terra dallo spazio.

Una cosa simile avviene in matematica: spesso è possibile imparare molto di più su un oggetto, uscendo fuori dallo spazio in cui esso è immerso.

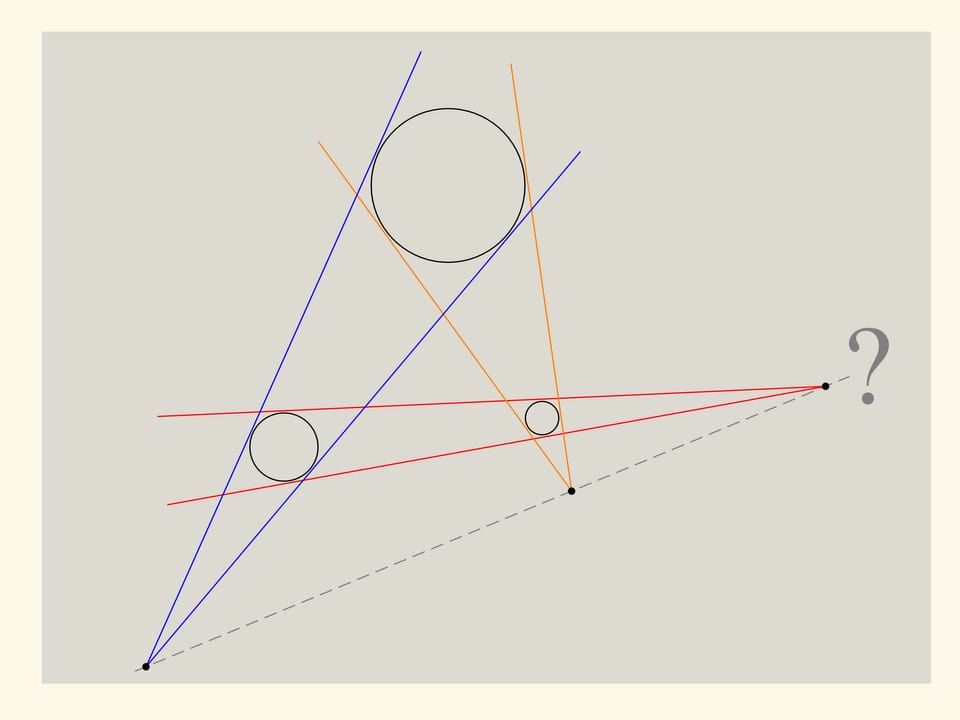
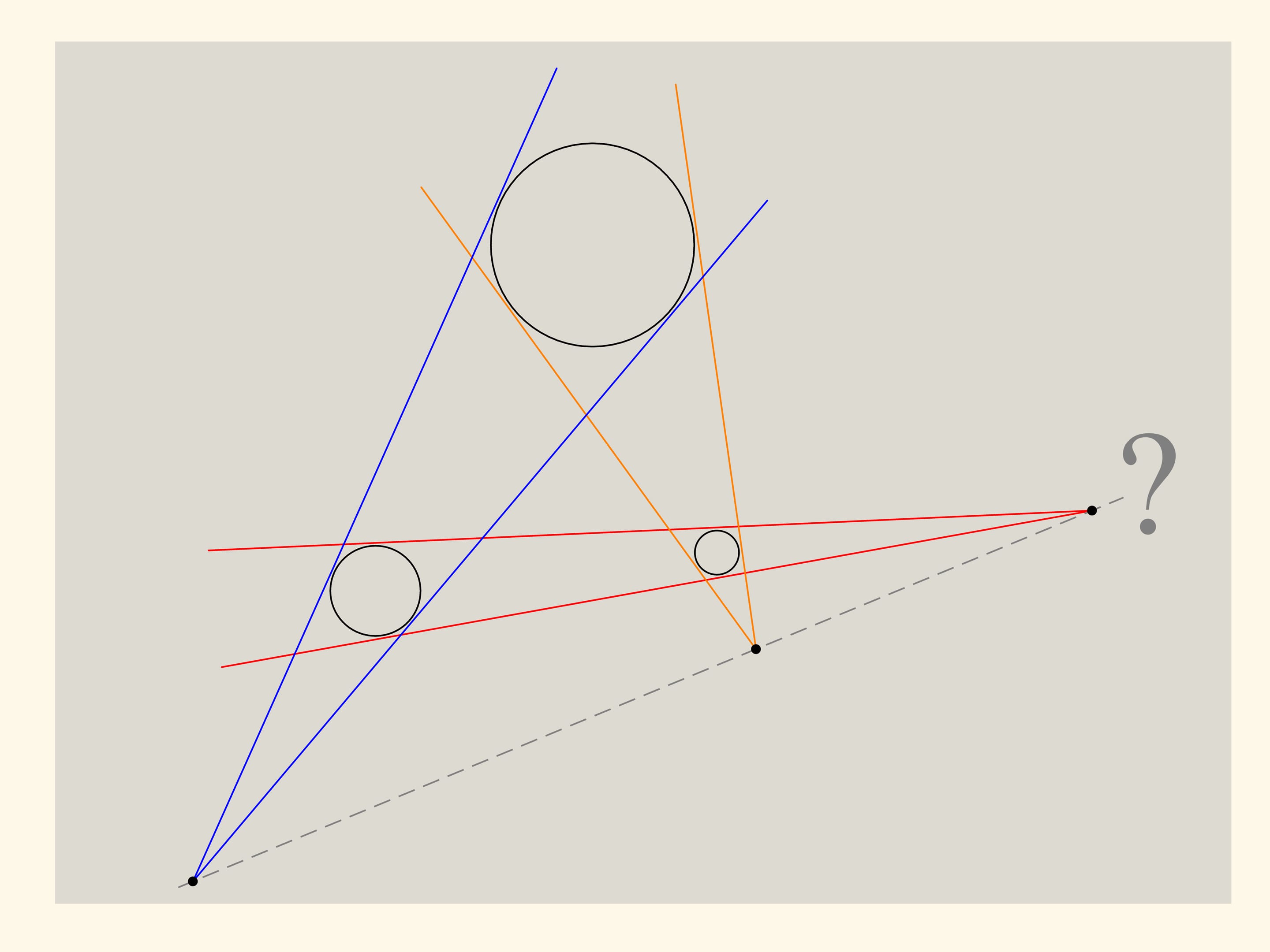
Consideriamo tre cerchi arbitrari in un piano e, per ogni coppia di questi cerchi, tracciamo due rette tangenti ad essi, e osserviamo i loro punti di intersezione. (Per ognuna di queste rette i cerchi tangenti devono stare nello stesso semipiano). Cosa possiamo dire sui tre punti di intersezione? A giudicare dalla figura, essi giacciono su di un’unica retta. Tuttavia una figura non è una dimostrazione, ma dà solo uno spunto per formulare una congettura. Cerchiamo di dimostrarla.

Il problema considerato è un problema di geometria piana. Ma osserviamo questo problema dal di fuori, cioè dallo spazio tridimensionale.

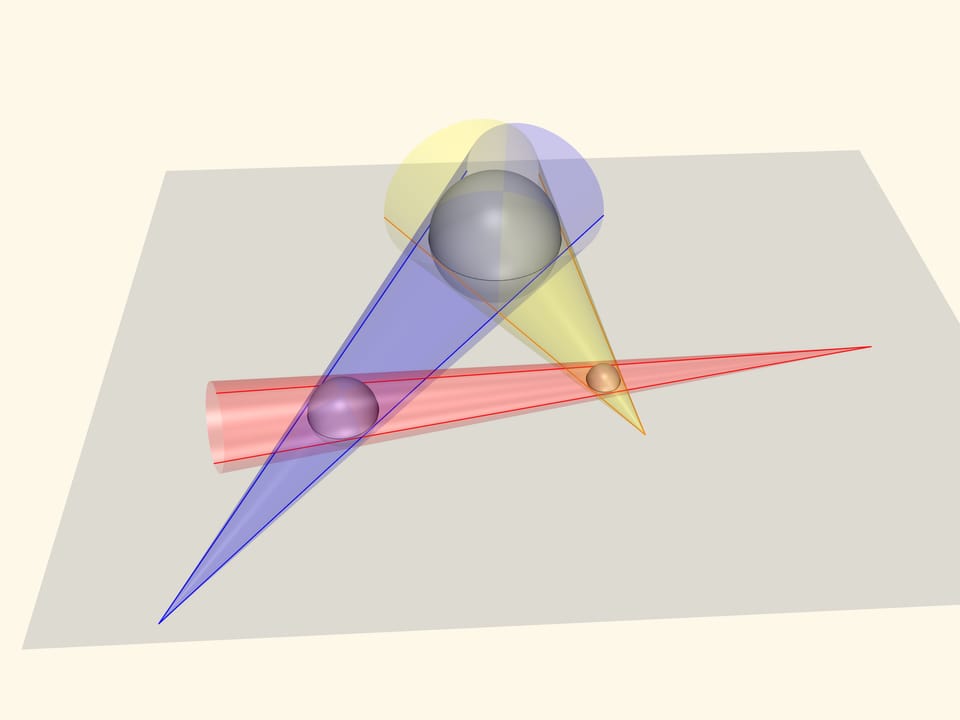
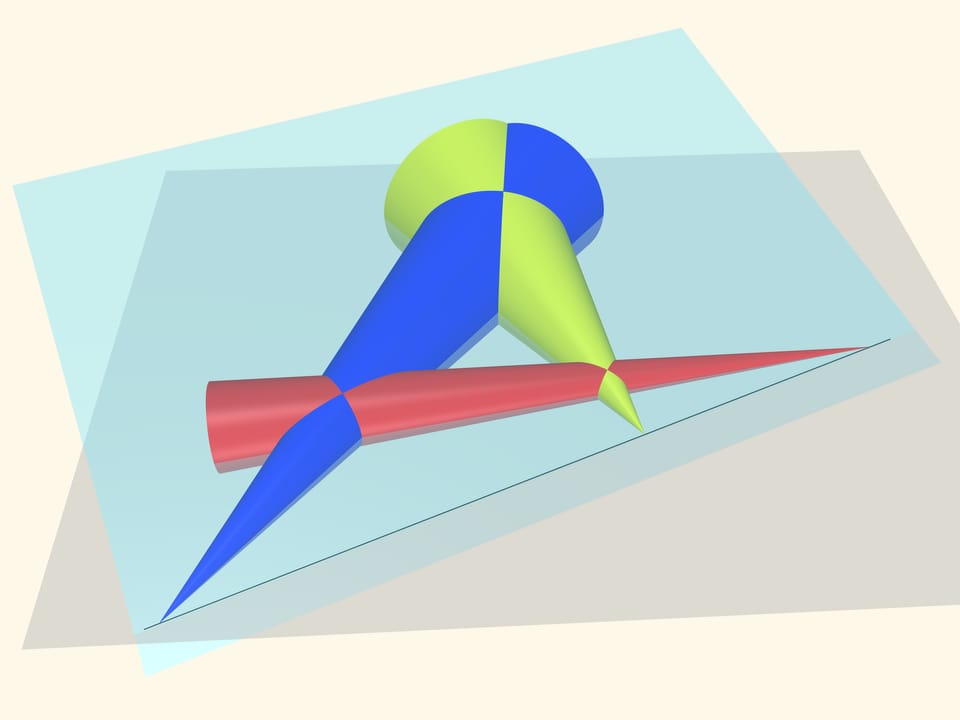
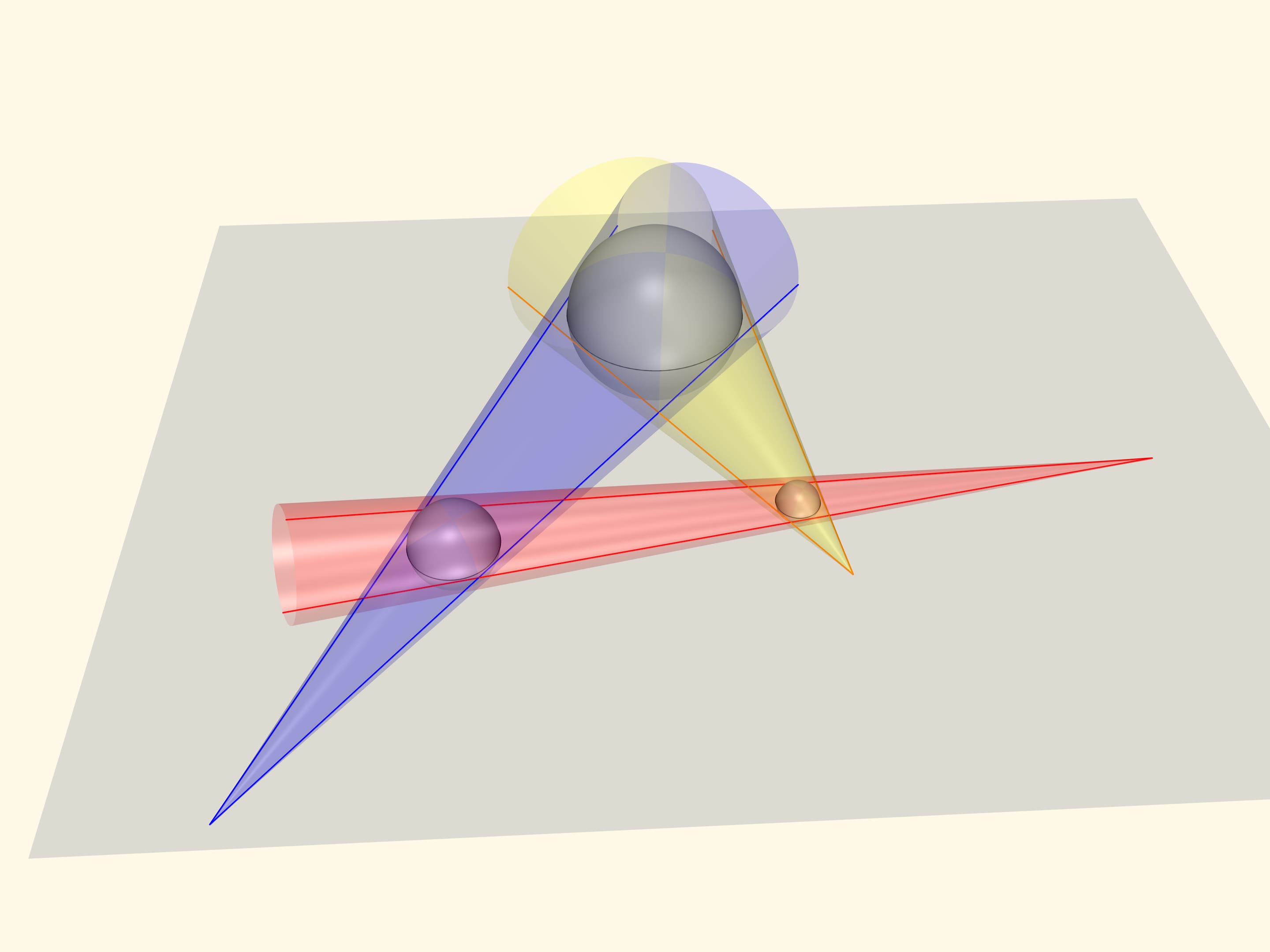
Costruiamo tre sfere nello spazio, in modo che i loro equatori siano proprio i nostri cerchi di partenza. Consideriamo tre coni, tangenti ognuno a una coppia di sfere. Le tangenti ai cerchi che abbiamo tracciato sono delle generatrici di questi coni. E i punti che, secondo la nostra congettura, stanno su una linea retta, sono i vertici di questi coni.

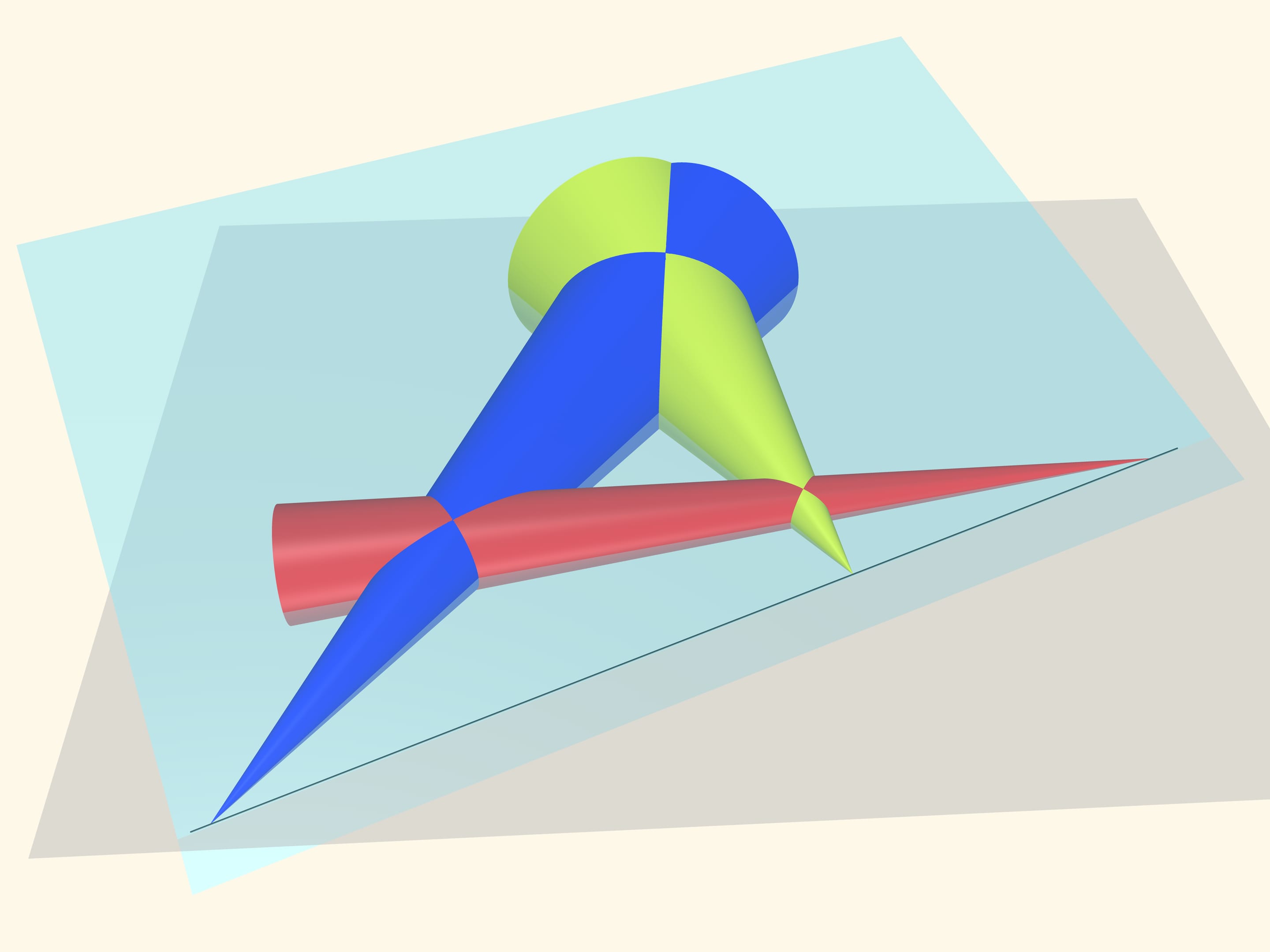
Ora posiamo un piano su questi coni. Le generatrici di questi coni che si trovano più in alto saranno tutte tangenti a questo piano, che esse definiscono univocamente. I punti che ci interes­sano, ossia i vertici dei coni, appartengono a questo piano, come anche al piano iniziale dei cerchi equatoriali. Ma due piani non paralleli si intersecano lungo una retta! Perciò, proprio come era stato ipotizzato, i punti di intersezione delle coppie di tangenti a tre cerchi arbitrari nel piano giacciono su di un’unica retta.

Questo teorema che ormai abbiamo dimostrato prende il nome da un matematico francese, Gaspard Monge.